Negli esercizi svolti sulla regola di Ruffini a seguire vedremo tutti i dettagli del procedimento di scomposizione. Nel seguito ricorderemo comunque la procedura e presenteremo un primo esercizio completamente guidato, nel quale compileremo la tabella passo dopo passo.
Per chi invece già conosce la regola di Ruffini ed ha fretta, è possibile passare direttamente agli esercizi successivi.
Allora, vediamo subito questi esercizi svolti sulla regola di Ruffini. 🙂
Esercizi svolti sulla regola di Ruffini: ripasso della regola di Ruffini
Ricerca di una radice per il polinomio da scomporre
Assegnato un polinomio di grado \( n \) del tipo:
\[ a_nx^n+a_{n-1}x^{n-1}+\dots+a_0 \]
un numero \( r \) è una sua radice se annulla il polinomio. Ovvero, \( r \) è una radice (o zero) del polinomio se sostituendo alla \( x \) il valore di \( r \) l’espressione del polinomio si annulla.
Ad esempio, dato il polinomio di terzo grado:
\[ -3x^3-2x+5 \]
il valore \( 1 \) è una sua radice poiché annulla il polinomio. Infatti, ponendo \( x=1 \) si ha:
\[ -3\cdot 1^3-2 \cdot 1+5 = 0 \]
Ora, il polinomio di partenza di grado \( n \) potrà essere scomposto come prodotto di un certo polinomio di grado \( n-1 \) e del binomio \( x-r \). Nel nostro caso, poiché \( r=1 \) il binomio sarà \( x-1 \).
Il problema è ora trovare il polinomio di grado \( n-1 \) (nel nostro caso, di grado \( 3-1=2 \)). Ed è qui che arriva a darci una mano la regola di Ruffini. 😉
Accorgimenti per la compilazione della tabella della regola di ruffini
L’idea è quella di costruire una particolare tabella. Prima di iniziare a compilarla, è fondamentale ordinare il polinomio da scomporre per potenze decrescenti. Non dimentichiamolo mai.
Fatto questo, scriveremo nella prima riga della tabella tutti i coefficienti del polinomio, ordinatamente, comprendendo anche ogni eventuale coefficiente nullo.
Così ad esempio, per il polinomio assegnato (il quale è già ordinato):
\[ -3x^3-2x+5 \]
scriveremo nella prima riga della tabella i coefficienti:
\[ -3 \quad 0 \quad -2 \quad 5 \]
Attenzione: lo zero è il coefficiente della \( x^2 \). Essa non compare nel polinomio ma nella tabella della regola di Ruffini dobbiamo esplicitamente indicare il coefficiente zero per i termini mancanti, sempre.
In altre parole, dobbiamo intendere il polinomio di partenza scritto in questo modo:
\[ -3x^3+0 \cdot x ^2-2x+5 \]
e considerare tra i coefficienti anche lo zero. 😉
Nel primo esempio a seguire spiegheremo nel dettaglio come compilare la tabella. Quello che ora è importante sottolineare, è che nella ricerca delle radici (o zeri) del polinomio, qui ci interessano unicamente radici intere o al massimo razionali (cioè, espresse come frazioni).
Ricerca della radici intere e razionali (frazionarie)
Le radici intere si ricercano per tentativi fra i divisori positivi e negativi del termine noto del polinomio di partenza.
Le radici razionali si ricercano tra le frazioni aventi per numeratore e denominatore rispettivamente i divisori positivi e negativi del termine noto e i divisori positivi del coefficiente del termine di grado massimo. Chiaramente, se nel polinomio da scomporre il coefficiente del termine di grado massimo è pari a \( 1 \), dovremo solo ricercare le radici intere.
Bene, possiamo cominciare! 🙂
Esercizi svolti sulla regola di Ruffini
Esercizio 1 (esercizio completamente guidato sulla regola di Ruffini)
Scomporre il polinomio:
\[ -3x^3-2x+5 \]
E’ il polinomio che già abbiamo cominciato ad esaminare. Sappiamo già che un suo zero (o radice) è il numero \( 1 \). Tuttavia, vediamo come è stato individuato.
cercare una radice del polinomio
Poiché il coefficiente del termine di grado massimo del polinomio è diverso da \( 1 \) (il coefficiente del termine \( -3x^3 \) è infatti pari a \( 3 \)), dobbiamo ricercare i valori della \( x \) che annullano il polinomio sia fra le radici intere, sia fra le radici frazionarie.
Precisiamo che ci serve un solo valore che annulla il polinomio. Per cui, conviene sempre partire dalla ricerca delle radici intere. E se troviamo un numero intero che annulla il polinomio siamo fortunati e ci fermiamo. Non c’è bisogno a quel punto di ricercare le radici razionali (frazionarie). Quest’ultime vanno ricercate solo se non riusciamo a trovare una radice intera del polinomio.
Nel nostro caso, dobbiamo ricercare una radice tra i divisori positivi e negativi del termine noto (\( 5 \)). Tali divisori sono:
\[ +5, \quad -5, \quad +1, \quad -1 \]
Ora, vediamo se fra questi valori riusciamo a trovarne almeno uno che annulla il polinomio. Si tratterà di provare ciascun valore sostituendolo alla \( x \) nel polinomio, finché non troveremo una radice:
\[ -3x^3-2x+5 \quad \text{con} \: x=-1 \quad \Rightarrow \quad -3 \cdot (-1)^3-2 \cdot (-1) + 5 \neq 0 \]
\[ -3x^3-2x+5 \quad \text{con} \: x=1 \quad \Rightarrow \quad -3 \cdot (1)^3-2 \cdot (1) + 5 = 0 \qquad \text{OK!} \]
Possiamo fermarci qui. 🙂 Il numero \( 1 \) è una radice del polinomio e questa ci basta per compilare la tabella della regola di Ruffini.
NOTA: per alleggerire i calcoli è in generale opportuno cercare le radici cominciando a fare i tentativi con i numeri più piccoli, via via provando successivamente con i numeri più grandi.
costruzione della tabella della regola di ruffini
A questo punto, riscriviamo il polinomio di partenza assicurandoci che sia ordinato per potenze di ordine decrescente (termini ordinati dal grado più grande a quello più piccolo), avendo cura di indicare esplicitamente i termini con coefficiente nullo. Si ha:
\[ -3x^3-2x+5=-3x^3+0x^2-2x+5 \]
Ora, compiliamo la prima riga della tabella scrivendo tutti i coefficienti del polinomio, compresi quelli nulli:

Nella seconda riga, a sinistra della prima linea verticale, scriviamo la radice del polinomio che abbiamo trovato:

Ora, nella terza riga (a destra della prima linea verticale), riportiamo il coefficiente del termine di grado massimo del polinomio:
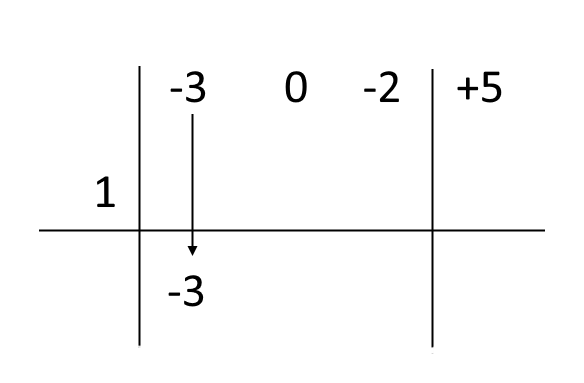
Ora, calcoliamo il prodotto tra la radice del polinomio e il coefficiente appena riportato (\( 1 \cdot (-3) = -3 \)). Scriviamo il risultato nella seconda riga, proprio sotto al secondo coefficiente del polinomio (sotto allo \( 0 \)):

Ora, nella terza riga, scriviamo il risultato della somma (algebrica) tra il secondo coefficiente del polinomio e l’ultimo numero appena scritto:

Infatti, \( 0+(-3)=-3 \). Si tratta in pratica di una somma algebrica fatta in colonna.
A questo punto, dobbiamo eseguire il prodotto tra la radice del polinomio e l’ultimo numero scritto. Così, \( 1 \cdot (-3) = -3 \). Scriviamo il risultato sotto al penultimo coefficiente del polinomio di partenza:

Ora, come facilmente intuibile, dovremo eseguire un’altra somma algebrica in colonna. In particolare, dovremo sommare tra loro i termini \( -2 \) e \( -3 \). Otteniamo: \( -2+(-3)=-5 \). Scriviamo il risultato nel posto ancora libero nella terza riga, proprio sotto i termini che abbiamo sommato tra loro:

La penultima mossa da fare è moltiplicare la radice del polinomio per l’ultimo numero scritto, e scrivere il risultato proprio sotto all’ultimo coefficiente del polinomio:

Ora non resta che eseguire la somma algebrica in colonna tra i termini \( +5 \) e \( -5 \). Il risultato che otteniamo è zero:
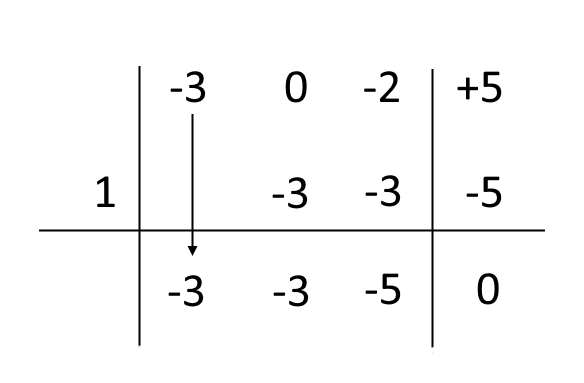
Il risultato dell’ultima somma algebrica in colonna deve sempre essere zero. Diversamente, abbiamo commesso degli errori nei calcoli oppure la radice che abbiamo usato non è in realtà una radice del polinomio. In quest’ultimo caso, dobbiamo assicurarci di trovare correttamente una radice del polinomio.
In generale, attenzione agli errori di segno. 😉
Ora, l’ultima riga della tabella è ciò che ci interessa, poiché contiene i coefficienti del polinomio di secondo grado che ci serve.
Scrivere la scomposizione del polinomio di partenza
Come detto, la regola di Ruffini ci permette di scomporre un polinomio di grado \( n \) come prodotto di un binomio di primo grado per un polinomio di grado \( n -1\). Nel nostro caso:
- il binomio di primo grado è dato da \( x-r \), ove \( r \) è la radice del polinomio usata nella tabella. Nel nostro caso, tale binomio è \( x-1 \);
- il polinomio di partenza è di terzo grado, per cui il polinomio che otteniamo con la regola di Ruffini è di secondo grado;
- i coefficienti del polinomio di secondo grado si trovano, in ordine, nell’ultima riga della tabella, proprio fra le due linee verticali.
Così, i coefficienti del polinomio di secondo grado sono:
\[ -3, \quad -3, \quad -5 \]
Il primo coefficiente a sinistra è il coefficiente del termine di secondo grado, il secondo coefficiente è quello del termine di primo grado mentre l’ultimo coefficiente è il termine noto (coefficiente del termine di grado zero). Allora, il polinomio di secondo grado cercato è:
\[ -3x^2-3x-5 \]
e il polinomio di partenza potrà essere scomposto come:
\[ \boxed{-3x^3-2x+5=(x-1)(-3x^2-3x-5)} \]
il risultato ottenuto presenta un polinomio che può essere ulteriormente scomposto?
Ora, nella scomposizione abbiamo un polinomio di secondo grado. In teoria, potrebbe essere possibile scomporlo utilizzando la regola del trinomio caratteristico. Tuttavia, con un po’ di tentativi ci si renderà conto che non è possibile effettuare la scomposizione. Per cui, la scomposizione già scritta è quella finale. 🙂
In generale, se il polinomio di grado \( n-1 \) presente nella scomposizione ottenuta può essere ulteriormente scomposto, bisognerà sempre effettuare tale scomposizione, utilizzando ancora la regola di Ruffini o preferibilmente un altro metodo se il polinomio è di secondo grado. Vedremo questo subito nell’esempio a seguire. 😉
Esercizio 2 (esercizi svolti sulla regola di Ruffini)
Scomporre il polinomio:
\[ y^3-6y^2+11y-6 \]
Ricerca di una radice del polinomio di partenza
Il coefficiente del termine di grado massimo è pari a \( 1 \) (infatti, \( y^3 = 1 \cdot y^3 \)) . Di conseguenza, dovremo cercare una radice del polinomio fra i soli divisori positivi e negativi del termine noto \( -6 \). Tali divisori sono:
\[ \pm1; \quad \pm 2;\quad \pm 3; \quad \pm 6 \]
Cerchiamo un numero tra questi valori tale che, sostituito alla \( x \), annulla il polinomio. Cominciamo a partire dai numeri più piccoli:
\[ y^3-6y^2+11y-6 \quad \text{con} \: x = 1 \quad \Rightarrow \quad 1^3-6 \cdot (1)^2+11 \cdot 1 -6= 0 \qquad \text{OK!} \]
Quindi siamo stati fortunati e abbiamo trovato subito una radice del polinomio, che è data dal valore \( 1 \).
tabella della regola di ruffini
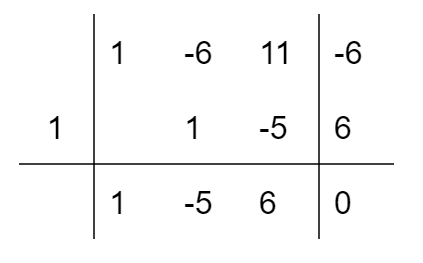
Vediamo per maggiore chiarezza di spiegare il significato di ciascun numero nella tabella:
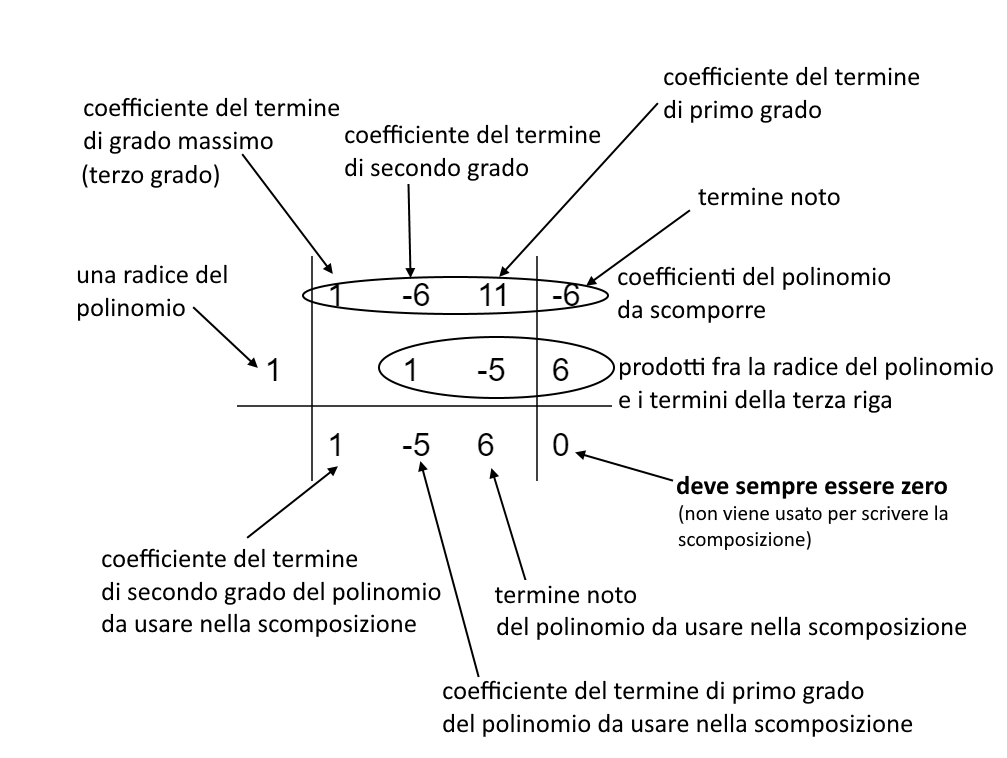
scriviamo la scomposizione per il polinomio di partenza
Come indicato nella tabella, i coefficienti del polinomio di secondo grado da utilizzare per la scomposizione sono:
\[ 1, \quad -5, \quad 6 \]
Così, il polinomio di secondo grado è:
\[ y^2-5y+6 \]
Poiché la radice del polinomio usata nella tabella è \( 1 \), il binomio di primo grado è:
\[ y-1 \]
Così, per il polinomio di terzo grado di partenza vale la scomposizione:
\[ y^3-6y^2+11y-6=(y-1)(y^2-5y+6) \]
Non abbiamo finito. Il polinomio di secondo grado può essere ulteriormente scomposto. Infatti, ricercando le radici intere vediamo che questo si annulla ad esempio per \( y=2 \). Ricordiamo sempre che se un polinomio di secondo grado ammette almeno una radice (intera o anche frazionaria), esso è scomponibile. Diversamente, non lo è.
E’ conveniente utilizzare per i polinomi di secondo grado il metodo di scomposizione del trinomio caratteristico, anche se è comunque possibile utilizzare ancora la regola di Ruffini.
Polinomio da scomporre:
\[ y^2-5y+6 \]
Cerchiamo due numeri la cui somma è \( -5 \) e il cui prodotto è \( +6 \). I numeri cercati sono \( -3 \) e \( -2 \). Così:
\[ y^2-5y+6=(y-3)(y-2) \]
Così la scomposizione finale del polinomio di partenza è data da:
\[ y^3-6y^2+11y-6=(y-1)(y-3)(y-2) \]
NOTA: i binomi \( y-3 \) e \(y-2 \) sono stati scritti mantenendo i segni della coppia di numeri trovata (\( -3 \) e \( -2 \)). Infatti, tali numeri derivano dalla regola del trinomio caratteristico e non sono radici del polinomio. Se invece vogliamo scomporre il polinomio usando le sue radici, dobbiamo scrivere i binomi invertendo i segni delle radici. Non a caso, nello scrivere il binomio di primo grado da usare nella scomposizione con la regola di Ruffini, dobbiamo invertire il segno della radice.
Verifica del risultato ottenuto
Come prova della correttezza della scomposizione, moltiplichiamo tra loro i tre binomi ottenuti, e vediamo se il risultato è uguale al polinomio di partenza:
\[ \begin{align}&(y-1)(y-3)(y-2)= \\ \\ & = y^3-3y^2-y^2+3y-2y^2+6y+2y-6= \\ \\ & = y^3+(-3-1-2)y^2+(3+6+2)y-6= \\ \\ & = y^3-6y^2+11y-6 \end{align} \]
Il risultato è corretto. 😉
Esercizio 3
Proseguiamo questa carrellata di esercizi svolti sulla regola di Ruffini. Ora andremo più spediti poiché il procedimento ormai è chiaro. Si tratta solo di assimilarlo meglio. 🙂 Proprio per questo, è utile che proviate a svolgere da soli gli esercizi, per poi confrontare il vostro svolgimento con quello proposto.
E’ inoltre importante osservare che il vostro procedimento potrebbe essere diverso ma comunque corretto. 😉 E’ infatti possibile che usiate nella tabella della regola di Ruffini una radice del polinomio diversa da quella utilizzata in questi esercizi svolti.
Scomporre il polinomio:
\[ 3x^4+8x^3+4x^2-3x-6 \]
Cerchiamo una radice anzitutto tra i divisori del termine noto \( -6 \). Poi, dato che il coefficiente del termine di grado massimo è diverso da \( 1 \), se non troviamo nessuna radice intera cercheremo le radici razionali.
I divisori positivi e negativi del termine noto sono:
\[ \pm1; \quad \pm 2; \quad \pm3; \quad \pm 6 \]
Cominciamo dai termini più piccoli:
\[ \begin{align}&3x^4+8x^3+4x^2-3x-6 \\ \\ & \text{con} \quad x=1: \\ \\ & \Rightarrow \quad 3 \cdot 1^4+8 \cdot 1^3 +4 \cdot 1^2-3 \cdot 1 – 6 \neq 0 \\ \\ & \text{con} \quad x = -1: \\ \\ & 3 \cdot (-1)^4+8 \cdot (-1)^3+4 \cdot (-1)^2-3 \cdot (-1) – 6 \neq 0 \\ \\ & \text{con}\quad x = -2: \\ \\ & \Rightarrow 3 \cdot (-2)^4+8 \cdot (-2)^3+4 \cdot (-2)^2-3 (-2) – 6 = 0 \qquad \text{OK}\end{align} \]
Quindi \( -2 \) è una radice del polinomio.
Possiamo a questo punto compilare la tabella:
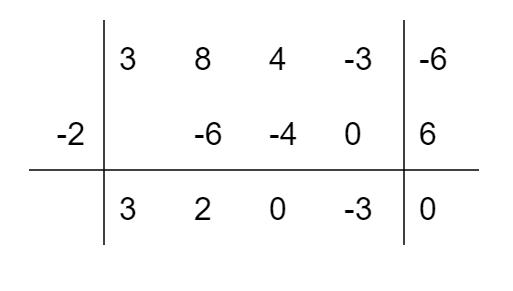
Attenzione: tra i termini nell’ultima riga della tabella abbiamo un coefficiente pari a zero. Esso corrisponde al termine di primo grado (il termine in \( x \)), il quale di conseguenza non comparirà nel polinomio di terzo grado.
Possiamo così scrivere per il polinomio di partenza la scomposizione:
\[ 3x^4+8x^3+4x^2-3x-6 = (x+2)(3x^3+2x^2-3) \]
Abbiamo finito? Per poterlo dire, dobbiamo vedere se il polinomio \( 3x^3+2x^2-3 \) può essere a sua volta scomposto.
Vediamo se esistono radici intere o al più razionali per questo polinomio. I divisori da testare sono i numeri:
\[ \pm 1; \quad \pm 3 \]
Questi valori comprendono anche i termini razionali (infatti, si ha ad esempio \( \dfrac{-3}{3}=-1 \), e quindi i termini razionali che qui si ottengono sono in realtà frazioni apparenti).
Sostituendo ciascun valore nella \( x \), vediamo che nessuno fa annullare il polinomio. Di conseguenza, la scomposizione è terminata, poiché se un polinomio non ha radici intere o razionali, non viene ulteriormente scomposto. 😉
Esercizio 4
Scomporre il polinomio:
\[ 2a^3-3a^2-7a+8 \]
Una radice del polinomio è data dal numero \( 1 \). Compiliamo la tabella:
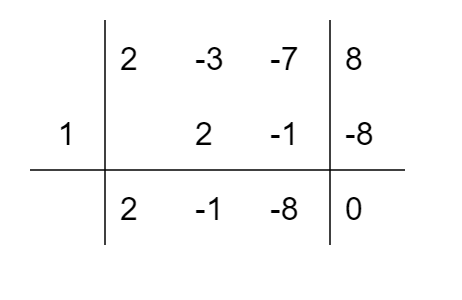
Abbiamo così la scomposizione:
\[ 2a^3-3a^2-7a+8=(a-1)(2a^2-a-8) \]
La scomposizione è quella finale poiché il polinomio \( 2a^2-a-8 \) non può essere scomposto.
NOTA: per capire se un polinomio di secondo grado può essere scomposto esiste un trucco. In particolare, scritto in generale un polinomio di secondo grado nella forma:
\[ ax^2+bx+c \]
il polinomio potrà eventualmente essere scomposto solo se:
\[ b^2-4\cdot a \cdot c \geq 0 \]
Diversamente, cioè se \( b^2-4ac < 0 \), il polinomio non può essere sicuramente scomposto.
Il termine \( b^2-4ac \) si chiama discriminante e viene utilizzato per la risoluzione delle equazioni di secondo grado (solitamente è argomento del secondo anno delle scuole superiori).
Attenzione: se \( b^2-4ac<0 \) siamo sicuri che il polinomio non può essere scomposto e non dobbiamo cercare nessuna radice, ma se \( b^2-4ac \geq 0 \) non possiamo dire nulla di certo. Il polinomio potrebbe essere scomponibile, ma non è detto. Infatti, il polinomio potrebbe avere radici irrazionali, le quali nel nostro contesto non ci interessano per la scomposizione.
E’ in ogni caso sempre possibile provare a ricercare le radici intere ed eventualmente razionali. Se nessun numero trovato annulla il polinomio, questo non è scomponibile.
E’ comunque importante chiarire che il discriminante così definito si può usare soltanto per polinomi di secondo grado. 😉 Nei polinomi di grado maggiore, per vedere se possono essere scomposti l’unica strada per noi è cercare le eventuali radici.
Esercizio 5
Veniamo all’ultimo esercizio di questa prima parte di esercizi svolti sulla regola di Ruffini. Scomporre il polinomio:
\[ 3t^4+5t^3+2t^2-3t-7 \]
Ancora una volta, conviene cercare le radici partendo dai numeri più piccoli. E in particolare, vediamo che una radice è data dal numero \( 1 \).
Compiliamo la tabella:
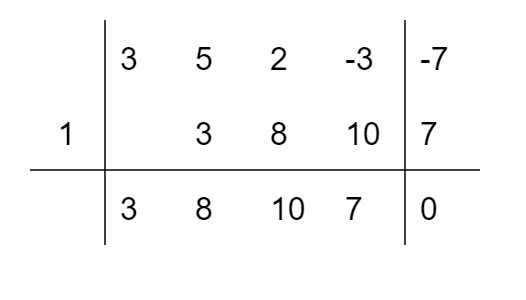
Vale la scomposizione:
\[ 3t^4+5t^3+2t^2-3t-7=(t-1)(3t^3+8t^2+10t+7) \]
Il polinomio di terzo grado nel prodotto ottenuto non può essere scomposto. Infatti, nessuno devi valori candidati ad essere radici annulla il polinomio (i valori da testare sono \( \pm 7, \: \pm \dfrac{7}{3} \)).
Così, la scomposizione ottenuta è quella finale. 🙂
Qui finisce la prima parte di questa serie di esercizi svolti sulla regola di Ruffini. Per chi vuole acquisire ulteriore dimestichezza con la regola di Ruffini e i relativi esercizi, è disponibile anche una seconda parte con altri esercizi svolti.
Vi ricordo infine il tool di scomposizione dei polinomi online, e soprattutto il tool per la scomposizione di polinomi con la regola di Ruffini, con passaggi. Con questi tool potrete verificare agevolmente i risultati dei vostri esercizi.
Ciao a tutti e come sempre buono studio con Altramatica! 🙂
