Il processo può eventualmente andare avanti, per cui il polinomio di secondo grado ottenuto potrà essere ulteriormente scomposto nel prodotto di due polinomi di primo grado. La regola di Ruffini può dunque essere reiterata.
Per chi già conosce la regola e vuole dedicarsi agli esercizi: esercizi svolti sulla regola di Ruffini. E se volete verificare i vostri risultati e la corretta costruzione della tabella: scomposizione con la regola di Ruffini online, con passaggi.
Utilità della regola di Ruffini
Vediamo di capire subito quale è l’utilità della regola di Ruffini relativamente alla scomposizione dei polinomi in modo pratico.
Ad esempio, dato il polinomio:
\[ x^3-7x+6 \]
questo potrà essere riscritto come prodotto di due polinomi, uno di primo grado e uno di secondo grado:
\[(x-1)(x^2+x-6)\]
A sua volta, il polinomio \( x^2+x-6 \) si può scomporre in:
\[ x^2+x-6 = (x-2)(x+3) \]
In conclusione, il polinomio inizialmente assegnato può essere espresso come prodotto di tre polinomi di primo grado:
\[ x^3-7x+6 = (x-1)(x-2)(x+3) \]
Questo tanto per chiarire dove vogliamo arrivare 😉 Ora tranquilli, vedremo nel dettaglio come effettuare questa scomposizione. La procedura è piuttosto meccanica e basta imparare poche e semplici regole 🙂
Per applicare la regola di Ruffini dobbiamo trovare almeno una radice del polinomio da scomporre
Dato un polinomio di grado \( n \) del tipo:
\[ a_{n}x^{n}+a_{n-1}x^{n-1}+…+a_{1}x+a_{0} \]
Se \( x_{1} \) è una radice del polinomio, cioè un valore della \( x \) che rende il polinomio nullo, allora il polinomio assegnato di grado \( n \) può essere scomposto come:
\[ (x-x_{1})Q(x) \]
ove \( Q(x) \) è un polinomio di grado \( n-1 \).
Dato ad esempio il polinomio di quarto grado:
\[ 3x^4+2x^3+x^2+x-1 \]
con un po’ di tentativi vediamo che il valore di \( x \) pari a -1 lo annulla. Possiamo dunque riscrivere il polinomio come:
\[ (x+1)Q(x) \]
ove \( Q(x) \) sarà un opportuno polinomio di terzo grado.
Il discorso è valido anche se abbiamo più radici del polinomio. Ad esempio, il polinomio:
\[ x^3-2x^2-43x+140 \]
ha come radici i valori:
\[ x_{1}=4; \qquad x_{2} = 5; \qquad x_{3} = -7 \]
E’ facile verificarlo, poiché sostituendo questi valori della \( x \) nel polinomio, questo si annullerà in tutti e tre i casi.
Ora, è possibile scomporre tale polinomio di terzo grado come prodotto di tre polinomi di primo grado, ciascuno della forma \( (x-x_{i}) \), ove \( x_{i} \) è una radice del polinomio da scomporre. Per cui avremo:
\[ x^3-2x^2-43x+140=(x-4)(x-5)(x+7) \]
In generale, se abbiamo un polinomio di grado \( n \) e conosciamo \( n \) radici di esso (\( x_{1}, x_{2}, … x_{n} \)), questo potrà essere espresso come il prodotto degli \( n \) termini \( (x-x_{i}) \).
Ovviamente, se dobbiamo scomporre un polinomio di quarto, terzo o anche secondo grado, determinarne per tentativi tutti i valori della \( x \) che lo annullano è improponibile. Ma vedremo che:
- esiste una semplice regola che ci permette di determinare pochi candidati tra i quali scegliere le radici del polinomio;
- esiste un’altra semplice regola che ci permette di scomporre il polinomio assegnato conoscendo soltanto una radice.
Le possibili radici di un polinomio
Assegnato un polinomio del tipo:
\[ a_{n}x^{n}+a_{n-1}x^{n-1}+…a_{1}x+a_{0} \]
le possibili radici del polinomio saranno tutti i termini \( \dfrac{p}{q} \), ove \( p \) e \( q \) sono divisori rispettivamente dei coefficienti \( a_{0} \) e \( a_{n} \) del polinomio. I termini \( p \) andranno presi con segno sia positivo, sia negativo. Invece, i termini \( q \) vanno considerati sempre con lo stesso segno (ad esempio, tutti con segno più).
Inoltre, se il termine del coefficiente di grado massimo del polinomio è pari a \( 1 \), sarà sufficiente ricercare le radici fra i divisori positivi e negativi del solo termine noto.
Assegnato così il polinomio:
\[ x^3-2x-1 \]
vediamo che il coefficiente del termine di grado massimo è pari a 1, perciò le possibili radici del polinomio sono i divisori positivi e negativi del termine noto -1, quindi -1 e 1.
Considerando dunque i due candidati \( -1 \) e \( +1 \), vediamo che il polinomio si annulla per \( x = -1 \), che è quindi radice del polinomio.
La regola di Ruffini: scomporre un polinomio di grado n conoscendo solo una sua radice
Vediamo ora il procedimento dettagliato della regola di Ruffini.
Dobbiamo dunque scomporre il polinomio:
\[ x^3-2x-1 \]
e sappiamo che una sua radice è -1. Il polinomio potrà essere quindi espresso come:
\[ x^3-2x-1 = (x+1)Q(x) \]
Finalmente, determineremo \( Q(x) \) 🙂
Occorre costruire una tabella come questa:

Come possiamo vedere, la tabella consiste nel tracciare tre linee. Nella prima riga, scriviamo i coefficienti del polinomio da scomporre, mettendo uno zero nel caso in cui il termine \( a_{n}x^{n} \) non sia presente nel polinomio.
Scriviamo i coefficienti ordinatamente, di modo che il coefficiente \( a_{0} \) vada a finire a destra della linea verticale.
Nella prima posizione a sinistra della seconda riga, a sinistra della linea verticale, scriviamo la radice \( r \) del polinomio che conosciamo.
Riscriviamo poi il termine \( a_{n} \) nella terza riga, a destra della linea verticale come indicato.
Nella posizione indicata dal quadratino blu, scriviamo il risultato del prodotto \( r \cdot a_{n} \).
Dovendo scomporre il polinomio \( x^3-2x-1 \) e conoscendo una sua radice, e cioè \( -1 \), cominceremo a compilare la tabella come segue:

Osserviamo che nel quadratino blu abbiamo scritto il prodotto \( -1 \cdot 1 \).
A questo punto, sommiamo tra di loro i due numeri presenti nella seconda colonna (\( 0 + (-1) \)) e scriviamo il risultato nella prima posizione disponibile sulla terza riga:

Ora, moltiplichiamo l’ultimo numero scritto (-1) per la radice del polinomio (-1). Scriviamo il risultato nella prima posizione disponibile sulla seconda riga.
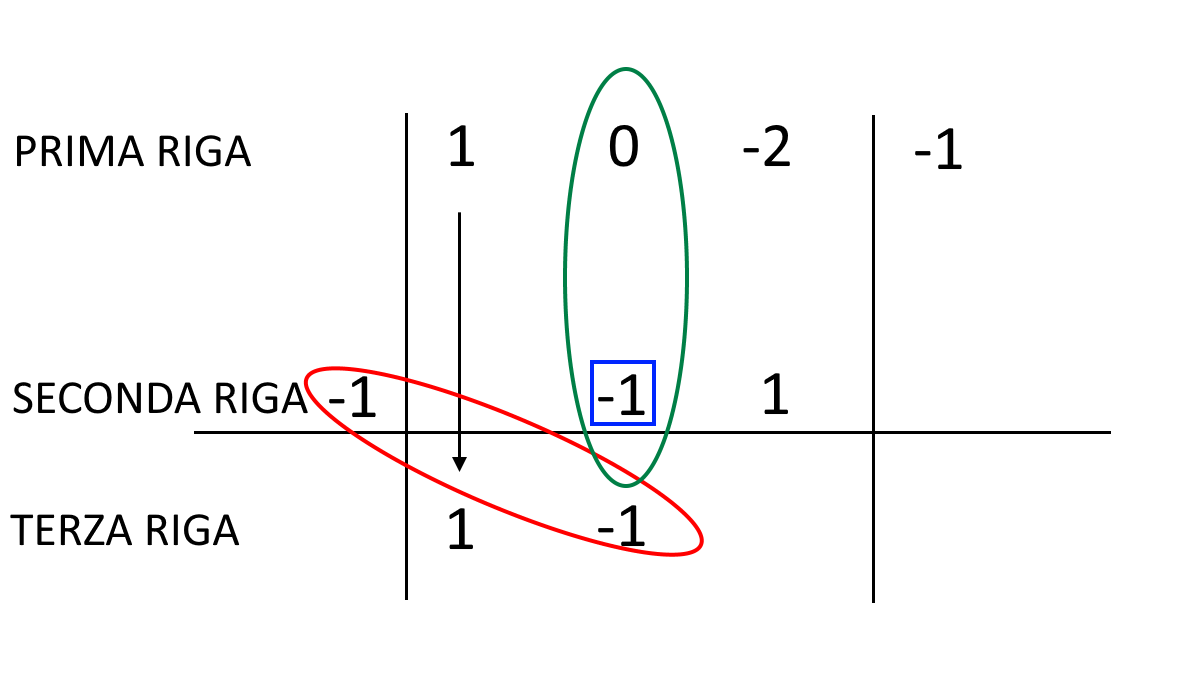
Ora, dobbiamo sommare tra loro i due numeri presenti nella terza colonna e scrivere il risultato (\( -2 +1 = -1 \)) nella prima posizione disponibile sulla terza riga:

Siamo quasi arrivati alla fine 😉 Ora, moltiplichiamo l’ultimo numero scritto (-1) per la radice (-1), e scriviamo il risultato nella prima posizione libera sulla seconda riga. Sommiamo i termini nella quarta colonna e scriviamo il risultato nell’ultima posizione della terza riga. Tale risultato deve essere sempre zero. Diversamente, abbiamo sbagliato qualcosa.

Ora, la terza riga ci offre, ordinatamente, i coefficienti del polinomio \( Q(x) \). Poiché il polinomio da scomporre è di terzo grado, \( Q(x) \) dovrà essere di secondo grado. Abbiamo dunque:
\[ Q(x) = x^2-x-1 \]
Possiamo finalmente scrivere:
\[ x^3-2x-1=(x+1)(x^2-x-1) \]
Abbiamo così scomposto il polinomio assegnato 🙂
Qui finisce la lezione sulla regola di Ruffini. Se ti interessano altri metodi di scomposizione dei polinomi, trovi tutto qui 🙂 Ricordo inoltre ancora una volta il comodissimo tool: scomposizione con la regola di Ruffini online con passaggi.
Sono inoltre disponibili le seguenti risorse contenenti molti esercizi svolti e commentati sulla regola di Ruffini:
Nella prossima lezione vedremo il Massimo Comune Divisore tra polinomi. Buono studio a tutti con Altramatica!

