Il procedimento da seguire non è gran che differente rispetto alla determinazione del massimo comune divisore tra numeri. Ma nel caso del massimo comune divisore tra polinomi, dovremo tenere conto della definizione di divisibilità tra polinomi. E questa presenta rispetto alla divisibilità tra numeri una differenza importante.
Senza ulteriori indugi, vediamo allora il concetto di massimo comune divisore tra polinomi anche mostrando degli esempi pratici.
Massimo comune divisore tra polinomi e divisibilità
Un numero si dice divisibile per un secondo numero se il resto della divisione tra il primo numero e il secondo numero è zero.
Per i polinomi la definizione è del tutto simile. Un polinomio \( A(x) \) è divisibile per un polinomio \( B(x) \) se il resto della divisione \( A(x):B(x) \) è zero. Il quoziente \( Q(x) \) sarà un polinomio che moltiplicato per il divisore \( B(x) \) restituirà il dividendo \( A(x) \).
Ora, nel caso dei numeri il quoziente che si ottiene dalla divisione tra due numeri è unico. Così ad esempio, data la divisione:
\[ 12:4 \]
il quoziente sarà pari a \( 3 \) e il resto sarà zero. Infatti, moltiplicando il quoziente per il divisore otteniamo il dividendo:
\[ 3 \cdot 4 = 12 \]
Consideriamo ora la divisione tra polinomi:
\[ (x^2+2x+1):(x+1) \]
Il quoziente che otteniamo è \( x+1 \) ed il resto è zero:

Moltiplicando il quoziente per il divisore otteniamo il polinomio dividendo:
\[ (x+1) \cdot (x+1) = x^2+2x+1 \]
Tuttavia, se proviamo a dividere lo stesso polinomio \( A(x) \) per il prodotto \( k \cdot B(x) \), ove \( k \) è un numero qualsiasi diverso da zero, otterremo comunque un resto zero: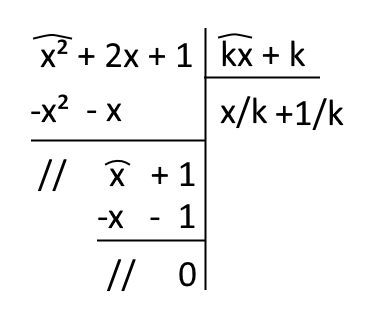
E ancora, moltiplicando il quoziente per il divisore otterremo ancora lo stesso polinomio \( A(x) \):
\[ \left(\dfrac{x}{k}+\dfrac{1}{k} \right)\cdot(kx+k)=x^2+2x+1 \]
Ciò significa che se un polinomio \( A(x) \) è divisibile per un polinomio \( B(x) \), allora esistono infiniti polinomi \( k\cdot B(x) \) che sono divisori di \( A(x) \).
Ora, ricercare il massimo comune divisore tra due o più polinomi equivale a ricercare il più grande polinomio che sia divisore di tutti i polinomi dati. Non otteniamo tuttavia un unico polinomio ma infiniti polinomi proprio a causa della costante moltiplicativa \( k \).
Ad esempio, consideriamo i polinomi:
\[ x^3+5x^2+7x+3; \qquad x^2+4x+3 \]
Per determinare il massimo comune divisore tra due numeri, la prima cosa da fare è scomporre i numeri dati in fattori primi. Allora, cominciamo scomponendo in fattori i polinomi assegnati.
Per il primo polinomio, useremo la regola di Ruffini:
\[ x^3+5x^2+7x+3=(x+1)(x+1)(x+3)= (x+1)^2(x+3) \]
Per il secondo polinomio, la regola del trinomio caratteristico:
\[ x^2+4x+3= (x+3)(x+1) \]
Ricordiamoci la definizione di massimo comune divisore tra numeri. L’MCD dei numeri dati si ottiene considerando il prodotto dei fattori comuni delle rispettive scomposizioni presi con il più piccolo esponente.
Così, avremo che:
\[ \text{MCD}[x^3+5x^2+7x+3, \: x^2+4x+3] = (x+1)(x+3)=x^2 +4x+3 \]
Tuttavia, questo non è l’unico risultato possibile. Ad esempio, la quantità:
\[ 2 \cdot (x^2 +4x+3) \]
sarà ancora il massimo comune divisore dei due polinomi assegnati. Infatti, per quanto osservato poc’anzi sulla divisione, anche questo polinomio divide entrambi i polinomi di partenza.
Come procediamo allora? In teoria, una qualunque costante moltiplicativa è accettabile. Di fatto, è buona pratica prendere come costante moltiplicativa l’MCD tra i fattori numerici presenti nelle scomposizioni dei polinomi di partenza.
In questo caso, poiché il fattore numerico di entrambi i polinomi di partenza “non appare” (ovvero è \( 1 \)), allora considereremo come MCD semplicemente il polinomio \( x^2 +4x+3 \). 😉
Esempi
ESEMPIO 1
Consideriamo i polinomi:
\[ 2x-2y, \qquad x^2-2xy+y^2 \]
Determiniamo il loro massimo comune divisore. La prima cosa da fare è scomporre i polinomi in fattori.
Il polinomio \(2x-2y\) si scompone effettuando un raccoglimento totale:
\[ 2x-2y= 2(x-y) \]
Il polinomio \( x^2-2xy+y^2 \) è un quadrato di un binomio. Infatti, compaiono i quadrati dei termini \( x \) e \( y \) e il loro doppio prodotto. Attenzione: il doppio prodotto è negativo per cui i due termini dovranno essere discordi. Avremo così ad esempio:
\[ x^2-2xy+y^2=(x-y)^2 \]
Si tratta ora di determinare il massimo comune divisore dei polinomi dati così scomposti. Si ha:
\[ \text{MCD}[ 2(x-y),(x-y)^2] =x-y \]
Abbiamo infatti preso il fattore comune \( (x-y) \) con il più piccolo esponente con il quale appare nelle scomposizioni (e cioè, \( 1 \)).
Riferendoci ai polinomi nella forma di partenza scriveremo quindi in conclusione:
\[ \text{MCD}(2x-2y, \: x^2-2xy+y^2)=x-y \]
ESEMPIO 2
Determinare il massimo comune divisore dei polinomi:
\[ 4x^3-4x^2+12x-12; \qquad 12x^2+48x-60 \]
Scomponiamo in fattori i polinomi. Per il primo polinomio useremo la regola di Ruffini, mentre per il secondo la regola del trinomio caratteristico:
\[ 4x^3-4x^2+12x-12=4 \cdot (x-1)(x^2+3) \]
\[12x^2+48x-60 = 12\cdot(x-1)(x+5)\]
Ora, i fattori comuni sono dati dal binomio \( x-1 \) e dal fattore numerico \( 4 \) (infatti, \( \text{MCD}(12, 4)=4 \)).
Così abbiamo in conclusione:
\[ \text{MCD}(4x^3-4x^2+12x-12, \: 12x^2+48x-60 ) = 4(x-1)\]
Per quanto riguarda la determinazione del massimo comune divisore tra polinomi è tutto. Vi ricordo che è disponibile il tool massimo comune divisore tra polinomi online, con il quale potrete verificare agevolmente i risultati dei vostri esercizi.
Nella prossima lezione vedremo il minimo comune multiplo tra polinomi.
Ciao a tutti e come sempre buono studio con Altramatica! 🙂
