In questa lezione, vedremo la divisione tra polinomi nei quali compare una sola lettera. Nella prossima lezione vedremo come comportarci nel caso di divisione tra polinomi con più lettere.
Effettueremo l’operazione di divisione tra due polinomi costruendo una opportuna tabella. E, come vedremo, l’operazione sarà ricondotta a divisioni, moltiplicazioni e somme algebriche tra monomi.
Prima di introdurre le regole pratiche per eseguire l’operazione, mostreremo cosa si intende per divisibilità tra due polinomi. E in particolare, chiariremo cosa succede quando i due polinomi sono divisibili e quando non lo sono.
Cominciamo allora subito questa lezione sulla divisione tra due polinomi. 🙂
Criterio di divisibilità tra polinomi
Nell’operazione di divisione tra due polinomi, richiediamo anzitutto che il polinomio dividendo sia di grado (complessivo) maggiore o al più uguale al grado (complessivo) del polinomio divisore.
Inoltre, richiediamo che il polinomio divisore sia diverso da zero.
Per cui, se il dividendo ha grado \( n \) e il divisore ha grado \( m \), il quoziente avrà grado \( n-m \).
Il polinomio \( A(x) \) è divisibile per il polinomio \( B(x) \) se esiste un polinomio quoziente \( Q(x) \) che, moltiplicato per \( B(x) \), restituisce il polinomio di partenza \( A(x) \).
Così, se il polinomio \( A(x) \) è divisibile per \( B(x) \) si ha:
\[ A(x)=Q(x) \cdot B(x) \]
e il quoziente \( Q(x) \) si dice completo.
Diversamente, se il polinomio \( A(x) \) non è divisibile per \( B(x) \), la divisione può comunque essere eseguita ma otterremo un resto \( R(x) \). In questo caso avremo:
\[ A(x)=Q(x) \cdot B(x) + R(x) \]
e il quoziente \( Q(x) \) si dirà incompleto.
Il grado del resto sarà sempre minore del grado \( m \) del divisore.
Osserviamo che ponendo \( R(x) = 0\) otteniamo la precedente relazione scritta nel caso in cui \( A(x) \) è divisibile per \( B(x) \). Così, possiamo affermare che se \( A(x) \) è divisibile per \( B(x) \) il resto della divisione \( R(x) \) è zero.
In caso di resto \( R(x) \) diverso da zero, è utile riscrivere la precedente relazione come:
\[ \dfrac{A(x)}{B(x)}=Q(x)+\dfrac{R(x)}{B(x)} \]
E’ stato sufficiente dividere entrambi i membri della relazione precedente per \( B(x) \). 😉
Così, noti \( Q(x) \) e \( R(x) \) è possibile esprimere il rapporto \( \dfrac{A(x)}{B(x)} \) proprio in funzione di quoziente e resto.
Se \( A(x) \) è divisibile per \( B(x) \) il resto \( R(x) \) è zero e la precedente diviene:
\[ \dfrac{A(x)}{B(x)}=Q(x) \]
Il quoziente viene quindi detto in questo caso completo poiché effettivamente equivale al rapporto tra i due polinomi di partenza e rappresenta quindi il risultato della divisione.
Regola per la divisione tra due polinomi
In generale, volendo eseguire la divisione \( A(x):B(x) \) bisogna prima di tutto assicurarsi che i polinomi \( A(x) \) e \( B(x) \) siano entrambi ordinati rispetto ad una data lettera.
Per il momento, lavoreremo con polinomi di una sola lettera. Per cui, i due polinomi \( A(x) \) e \( B(x) \) dovranno essere ordinati rispetto alla lettera esistente.
Inoltre, se nel polinomio dividendo \( A(x) \) abbiamo coefficienti nulli, questi dovranno essere indicati esplicitamente. Così ad esempio, se abbiamo il polinomio:
\[ x^3+2x+7 \]
questo andrà riscritto come:
\[ x^3+0x^2+2x+7 \]
o in alternativa, come più comunemente viene fatto:
\[ x^3+0+2x+7 \]
Proviamo ora ad eseguire la divisione:
\[ (3x^3+6x^2-x-2):(3x^2-1) \]
I polinomi risultano già ordinati e non abbiamo coefficienti nulli nel polinomio dividendo (il primo polinomio), per cui possiamo direttamente utilizzare i polinomi così come sono.
Rappresentiamo la divisione in forma tabellare:
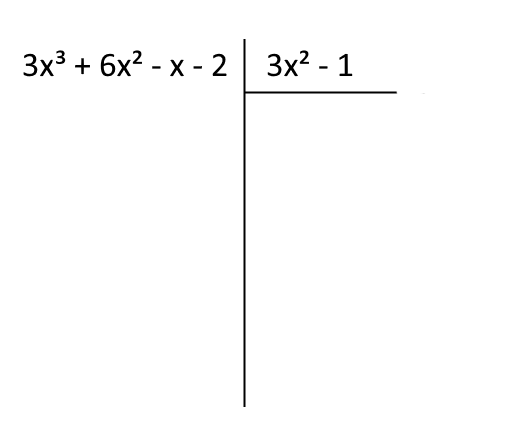
Dividiamo il primo termine del polinomio dividendo per il primo termine del polinomio divisore. Si tratta così di eseguire la divisione \( (3x^3):3x^2 \), cioè la divisione tra il primo monomio nel dividendo e il primo monomio nel divisore. Scriviamo il risultato proprio sotto al primo termine del divisore:
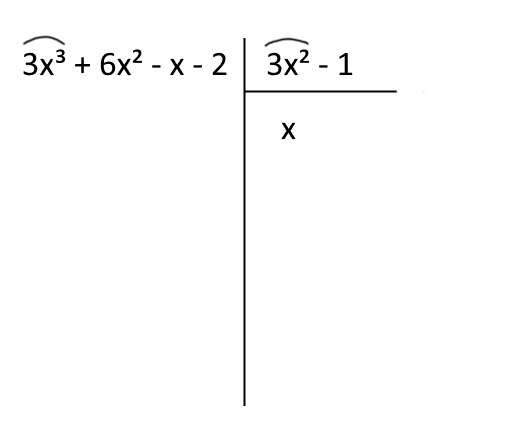
Abbiamo così ottenuto il primo termine del quoziente. Moltiplichiamo ora quest’ultimo \( (x) \) per ciascuno dei termini del divisore. Si tratterà così di eseguire delle moltiplicazioni tra monomi. Scriviamo ciascun risultato ordinatamente sotto i termini del polinomio dividendo dello stesso grado, avendo cura di invertire i segni dei risultati ottenuti. Si ha:

Prestiamo attenzione a come abbiamo incolonnato i termini. Un termine in \( x^3 \) è sotto ad un altro termine in \( x^3 \), un termine in \( x \) è sotto ad un altro termine in \( x \). Al posto del termine in \( x^2 \) mancante abbiamo lasciato uno spazio vuoto. Ciò nell’ottica di sommare in colonna tra loro monomi simili.
Ora, tiriamo una riga orizzontale come a sottolineare gli ultimi termini scritti, fermandoci in corrispondenza della linea verticale. Eseguiamo quindi la somma algebrica tra i termini del polinomio dividendo e i monomi scritti proprio sotto di essi. Gli spazi vuoti vanno considerati come termini zero. Si ha così:
Il polinomio che abbiamo appena scritto rappresenta un resto parziale. Dobbiamo procedere con la divisione poiché il suo grado non è ancora minore rispetto a quello del polinomio divisore.
Dividiamo ora il primo termine dell’ultimo polinomio scritto sempre per il primo termine del polinomio divisore. Dobbiamo quindi eseguire la divisione tra monomi\( (6x^2):(3x^2) \). Scriviamo il risultato ottenuto completo di segno a seguire il primo termine del quoziente:
Ora, moltiplichiamo il secondo termine del quoziente appena scritto per ciascun termine del polinomio divisore. Scriviamo i risultati ottenuti ordinatamente sotto ciascun termine del resto parziale dello stesso grado, ancora una volta avendo cura di invertire i segni:

Come fatto in precedenza, tiriamo ancora una riga orizzontale proprio sotto agli ultimi termini scritti. Eseguiamo quindi le somme algebriche in colonna fra i termini simili: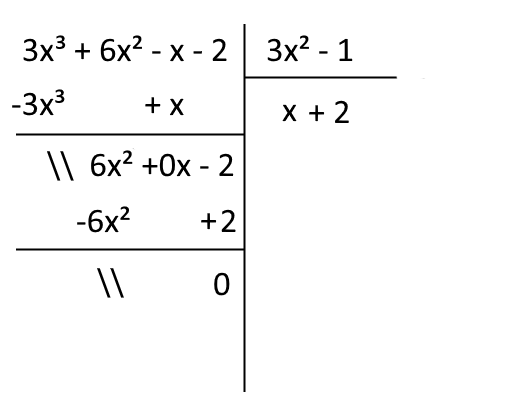
Osserviamo che abbiamo ottenuto un resto pari a zero. I due polinomi sono allora divisibili e il polinomio \( x+2 \) rappresenta il quoziente completo della divisione.
E come è immediato verificare:
\[ A(x)=Q(x)\cdot B(x) \]
infatti l’uguaglianza:
\[ 3x^3+6x^2-x-2=(x+2)\cdot (3x^2-1) \]
è vera poiché:
\[ (x+2)\cdot (3x^2-1) = 3x^3-x+6x^2-2=3x^3+6x^2-x-2 \]
L’idea che sta dietro alla regola della divisione tra polinomi
L’algoritmo (ovvero il procedimento) che sta dietro alla divisione tra polinomi si basa sul calcolare dei particolari quozienti parziali, moltiplicarli per il polinomio divisore, e sottrarre via via i risultati ottenuti al polinomio dividendo e ai vari resti parziali. Il procedimento si ferma quando otteniamo un resto zero (nel caso di polinomi divisibili) o un resto di grado inferiore a quello del polinomio divisore.
I “particolari quozienti parziali” sono proprio i quozienti che via via si ottengono eseguendo le varie divisioni tra monomi.
E’ interessante osservare che ciascuna parte letterale presente nei polinomi dividendo e divisore rappresenta un particolare ordine di grandezza. Così ad esempio seguendo la procedura indicata è possibile eseguire anche una divisione tra numeri, esprimendo sia il dividendo, sia il divisore in forma polinomiale. Ad esempio, consideriamo la divisione:
\[ 356:17 \]
Scriviamo entrambi i numeri in forma polinomiale:
\[ (3 \cdot 10^2+ 5 \cdot 10 + 6):(1 \cdot 10+7) \]
Come vediamo, ciascuna cifra numerica è moltiplicata per il corrispondente ordine di grandezza. Proviamo ad eseguire la divisione con la tabella in modo simile a quanto fatto in precedenza. Trattiamo le potenze di \( 10 \) come se fossero parti letterali, applicando le proprietà delle potenze come usualmente facciamo:

Così, il risultato della divisione \( 356:17 \) è \( 3 \cdot 10 -16= 14 \) con resto \( 118 \). Ha senso quanto scritto? Sì. 🙂 Infatti, se utilizziamo la relazione:
\[ \dfrac{A(x)}{B(x)}=Q(x)+\dfrac{R(x)}{B(x)} \]
con l’avvertenza che ora non abbiamo polinomi in funzione di \( x \) ma quantità numeriche, si ha:
\[ 356:17= 14 + \dfrac{118}{17} \approx 20,9411765 \]
ed effettivamente eseguendo la divisione direttamente tra i numeri di partenza otteniamo:
\[ 356:17=20,9411765 \]
E ci siamo. 😉
L’esempio numerico mostrato vuole far capire il principio che sta dietro alla regola della divisione fra due polinomi. Ed in particolare vogliamo sottolineare l’importanza di ordinare sempre i polinomi prima di eseguire la divisione e di indicare sempre esplicitamente gli eventuali coefficienti nulli del polinomio dividendo. Il tutto, facendo sempre in modo che vengano eseguite somme algebriche in colonna solo tra monomi simili, ovvero tra quantità aventi lo stesso ordine di grandezza.
Per questa lezione introduttiva sulla divisione tra due polinomi è tutto. Per verificare i risultati degli esercizi, potete utilizzare questo pratico tool: divisione tra polinomi online (una variabile).
Nella prossima lezione vedremo la divisione fra polinomi aventi anche più lettere.
Un saluto a tutti voi! 🙂
