La prima definizione che occorre esaminare per poter comprendere la divisione tra polinomi con più lettere è quella di polinomio ordinato. Abbiamo già visto la definizione di polinomio ordinato in una precedente lezione, tuttavia la riprenderemo brevemente anche qui. 🙂
Poiché in particolare è possibile ordinare un polinomio rispetto ad una qualsiasi fra le lettere che contiene, il problema è proprio capire rispetto a quale lettera ordinare i polinomi tra i quali si deve effettuare la divisione.
Vedremo ora di chiarire tutto questo, fornendo anche esempi. Per cui, mettiamoci comodi e vediamo insieme come eseguire la divisione tra polinomi con più lettere. 🙂
Rispetto a quale lettera ordinare i polinomi per la divisione?
Riprendiamo brevemente la definizione di polinomio ordinato. In particolare, ci riferiremo al caso di polinomi ordinati per potenze decrescenti, poiché è questo il caso di interesse per la divisione.
Finché abbiamo una sola lettera, non abbiamo problemi. Ad esempio, consideriamo il polinomio:
\[ 3x^3+7-2x^2 \]
Tale polinomio si dirà semplicemente ordinato (secondo le potenze decrescenti) una volta che lo scriveremo in questo modo:
\[ 3x^3-2x^2+7\]
Infatti, nei monomi abbiamo esponenti per la lettera \( x \) decrescenti da sinistra verso destra.
Ora, consideriamo invece il polinomio:
\[ 2y^2+3a^2 -ay \]
Per come si presenta, non è ordinato rispetto a nessuna lettera. Ed abbiamo due strade da scegliere. Possiamo ad esempio ordinarlo rispetto alla lettera \( y \):
\[ 2y^2-ay+3a^2 \]
o rispetto alla lettera \( a \):
\[ 3a^2-ay+2y^2 \]
Ora, supponiamo di voler dividere il polinomio \( 4y^3+6ay^2+10a^2y+9a^3 \) per il polinomio \( 2y^2+3a^2 -ay \). Ovvero, consideriamo la divisione:
\[ (4y^3+6ay^2+10a^2y+9a^3):(2y^2+3a^2 -ay ) \]
Osserviamo che il primo polinomio (il dividendo) ha grado complessivo \( 3 \) mentre il secondo polinomio (il divisore) ha grado complessivo (o semplicemente, grado) \( 2 \). Il quoziente avrà allora grado \( 3-2=1 \) e il resto avrà grado minore del divisore, e quindi grado minore di \( 2 \).
Come procediamo? Come intuibile, possiamo ordinare entrambi i polinomi rispetto alla lettera \( y \), oppure rispetto alla lettera \( a \). Nei rispettivi casi otterremo due distinte operazioni di divisione, entrambe eseguibili. L’importante è ordinare tutti e due i polinomi per la stessa lettera.
La divisione con i polinomi ordinati rispetto ad \( y \) è:
\[ (4y^3+6ay^2+10a^2y+9a^3):(2y^2-ay+3a^2 ) \]
mentre quella con i polinomi ordinati rispetto ad \( a \) è:
\[ (+9a^3+10a^2y+6ay^2+4y^3):(3a^2-ay+2y^2) \]
La domanda è chiara: quale delle due divisioni eseguiamo? E inoltre, le due divisioni forniscono gli stessi quozienti e resto oppure no?
Si può dimostrare che se una delle due divisioni fornisce un resto pari a zero, allora entrambe le divisioni avranno resto zero e stesso quoziente. Diremo cioè in tal caso che il polinomio dividendo è divisibile per il polinomio divisore, a prescindere dalla lettera rispetto alla quale saranno ordinati entrambi i polinomi.
Diversamente, se eseguendo una delle due divisioni otteniamo un resto diverso da zero, allora le due divisioni avranno i loro rispettivi quozienti e resto. Per cui, le due divisioni forniranno un differente quoziente.
In conclusione per eseguire la divisione tra polinomi con più lettere abbiamo le seguenti alternative:
- ordinare entrambi i polinomi secondo la stessa lettera che viene indicata nel testo dell’esercizio;
- in caso di mancata indicazione nel testo, precisare noi rispetto a quale lettera intendiamo ordinare i polinomi per la divisione. Se il resto che otteniamo una volta eseguita la divisione rispetto alla lettera scelta è diverso da zero, sapremo che quoziente e resto calcolati sono un risultato valido soltanto se i polinomi sono ordinati rispetto a quella lettera.
Osserviamo che le divisioni possibili sono tante quante sono le differenti lettere che figurano nei polinomi. Quindi.. in caso di polinomi con molte lettere conviene sicuramente sceglierne una! 🙂
Un primo esempio relativo alla divisione tra due polinomi con più lettere
Eseguiamo la divisione scritta poco fa:
\[ (4y^3+6ay^2+10a^2y+9a^3):(2y^2-ay+3a^2 ) \]
Scegliamo di dividere rispetto alla variabile (lettera) \( y \). Osserviamo subito che entrambi i polinomi sono già ordinati rispetto a tale lettera.
Ora, poiché la variabile che consideriamo è la \( y \), dovremo vedere la lettera \( a \) come un numero, ovvero un parametro facente parte del coefficiente di ciascun monomio in \( y \).
Così ad esempio vedremo il termine \( 6ay^2 \) come un monomio avente parte letterale \( y^2 \) e come coefficiente il termine \( 6a \). Possiamo in altre parole vedere \( 6a \) come la “parte numerica” del monomio considerato, il cui valore dipende dal parametro \( a \).
In virtù di questi ragionamenti, possiamo anche affermare che i termini \( 9a^3 \) e \( 3a^2 \) sono i “termini noti” rispettivamente del polinomio dividendo e divisore. Infatti, in questi termini non compare la variabile y che stiamo considerando e il loro valore dipende solo dal parametro \( a \). Per cui, tratteremo anche questi termini come se fossero numeri.
Così, possiamo evidenziare nella divisione assegnata le quantità che dovremo considerare “numeri”:
\[ (\boxed{4}y^3+\boxed{6a}y^2+\boxed{10a^2}y+\boxed{9a^3}):(\boxed{2}y^2-\boxed{a}y+\boxed{3a^2} ) \]
Precisiamo: nei calcoli potremo eseguire le operazioni tra monomi come sempre. Il fatto che abbiamo una variabile e un parametro non fa cambiare nulla da questo punto di vista. La distinzione tra variabile e parametro sarà fondamentale invece, come vedremo tra un istante, nel valutare il grado dei resti parziali e del divisore.
Ora veniamo finalmente ai calcoli. 🙂 La procedura è del tutto simile a quella vista per la divisione dei polinomi di una sola variabile. In ogni caso, vedremo come svolgere l’operazione passo per passo.
Impostiamo come al solito la tabella della divisione:

Cominciamo eseguendo la divisione tra il primo termine del polinomio dividendo e il primo termine del polinomio divisore. Scriviamo il risultato sotto al primo termine del polinomio divisore. Tale risultato sarà il primo termine del quoziente.

Ora procediamo moltiplicando il monomio appena scritto per ciascun termine del polinomio divisore, scrivendo i risultati via via ottenuti sotto a ciascun termine simile del polinomio dividendo, avendo cura di invertire il loro segno. Così avremo:

Ora tiriamo una riga orizzontale come a sottolineare i termini appena scritti, fermandoci una volta che incontriamo la linea verticale. Eseguiamo poi la somma algebrica in colonna tra i termini del polinomio dividendo e gli ultimi termini scritti. Consideriamo lo spazio vuoto come un termine zero. Il risultato di tale somma sarà un resto parziale.

Osserviamo che il grado rispetto alla lettera \( y \) del resto parziale ottenuto non è ancora minore del grado rispetto alla lettera \( y \) del polinomio divisore. Di conseguenza, dovremo proseguire la divisione.
Perché abbiamo ragionato con il grado rispetto alla lettera \( y \) e non con il grado complessivo? Perché, come detto, dobbiamo considerare la lettera \( a \) come un parametro facente parte del coefficiente di ciascun termine. Nel valutare il grado del resto e quello del divisore consideriamo pertanto il grado riferito alla variabile rispetto alla quale abbiamo inizialmente ordinato i polinomi e non il grado complessivo. 😉
Procediamo allora dividendo il primo termine del resto parziale per il primo termine del polinomio divisore. Scriviamo il risultato ottenuto completo del suo segno, a seguire il primo termine del quoziente:
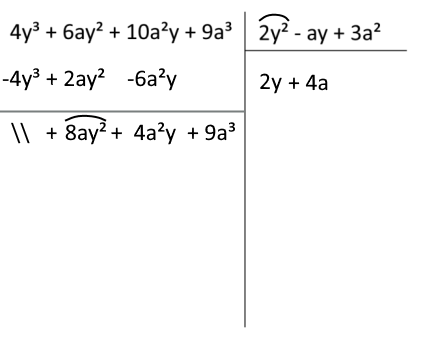
Ora moltiplichiamo l’ultimo monomio scritto (\( 4a \)) per ciascun termine del polinomio divisore. Come in un precedente passaggio, scriviamo i risultati via via ottenuti sotto ai termini simili del resto parziale, ancora avendo cura di invertire i loro segni:

Ora, tiriamo un’altra linea orizzontale ed eseguiamo la somma algebrica in colonna tra i termini del resto parziale e gli ultimi termini scritti:

Il grado rispetto alla lettera \( y \) del resto ottenuto è minore del grado ancora rispetto alla lettera \( y \) del polinomio divisore. Possiamo allora dire che la divisione è terminata e abbiamo ottenuto un quoziente pari a \( 2y+4a \) e un resto pari a \( 8a^2y-3a^3 \).
Per controllare il risultato utilizzeremo la relazione:
\[ A(y)=Q(y) \cdot B(y)+R(y) \]
ove \( A(y) \) è il polinomio dividendo, \( B(y) \) è il polinomio divisore, \( Q(y) \) è il quoziente e \( R(y) \) è il resto. Per chiarezza, usando queste quantità la divisione sarà indicata come \( A(y):B(y) \).
Osserviamo che pur avendo anche la lettera \( a \) nei polinomi dividendo e divisore intendiamo le quantità in funzione della sola variabile \( y \), cioè la variabile rispetto alla quale abbiamo ordinato i polinomi dividendo e divisore.
Poiché nel nostro caso \( A(y)= 4y^3+6ay^2+10a^2y+9a^3\), \( B(y)=2y^2-ay+3a^2 \), \( Q(y)=2y+4a \) e \( R(y)= 8a^2y-3a^3 \) abbiamo per la verifica:
\[ \begin{align}& Q(y)\cdot B(y)+R(y)=(2y+4a)\cdot(2y^2-ay+3a^2)+8a^2y-3a^3= \\ \\ & = 4y^3-2ay^2+6a^2y+8ay^2-4a^2y+12a^3+8a^2y-3a^3= \\ \\ & = \boxed{ 4y^3+6ay^2+10a^2y+9a^3}=A(y)\end{align} \]
Ed effettivamente ci siamo: il quoziente e il resto calcolati sono corretti. 🙂
Poiché il resto ottenuto è diverso da zero, per le considerazioni fatte ci aspettiamo che la divisione con gli stessi polinomi dati ma ordinati rispetto alla lettera \( a \) fornirà come risultato un quoziente e un resto diversi da quelli ottenuti ora.
Vediamolo subito eseguendo la divisione tra i due polinomi, stavolta ordinati rispetto alla lettera \( a \). Dobbiamo ora considerare la lettera \( a \) come variabile e la lettera \( y \) come parametro facente parte dei coefficienti dei termini nei polinomi.
Dovremo così calcolare la divisione:
\[ (9a^3+10a^2y+6ay^2+4y^3):(3a^2-ay+2y^2) \]
Come possiamo vedere, ora i polinomi dividendo e divisore risultano ordinati rispetto alla lettera \( a \) (lo ricordiamo, per potenze decrescenti).
Per meglio capire come stiamo procedendo, possiamo rappresentare i polinomi nel seguente modo:
\[ (\boxed{9}a^3+\boxed{10y}a^2+\boxed{6y^2}a+\boxed{4y^3}):(\boxed{3}a^2-\boxed{y}a+\boxed{2y^2}) \]
Quindi, nell’effettuare la divisione confronteremo il grado rispetto alla variabile \( a \) di ogni resto via via ottenuto con il grado rispetto alla variabile \( a \) del polinomio divisore . Ciò equivale a procedere in modo del tutto simile a quanto fatto per la precedente divisione. 😉
Eseguiamo i calcoli:

Come possiamo vedere, il quoziente e il resto ottenuti sono differenti rispetto a quelli della precedente divisione, pur trattandosi degli stessi polinomi dividendo e divisore. Comprendiamo quindi al lato pratico l’importanza di chiarire sempre rispetto a quale variabile ordiniamo i polinomi. 😉
Possiamo indicare la divisione eseguita con \( A(a):B(a) \) (ora la variabile considerata è \( a \)). Potremo così verificare il quoziente e il resto ottenuti mediante la relazione:
\[ A(a)=Q(a) \cdot B(a)+ R(a) \]
E quindi:
\[ \begin{align}& Q(a) \cdot B(a)+R(a) = (3a+\dfrac{13}{3}y)\cdot(3a^2-ay+2y^2)+\dfrac{13}{3} ay^2-\dfrac{14}{3}y^3= \\ \\ & = 9a^3-3a^2y+6ay^2+13a^2y-\dfrac{13}{3}ay^2+\dfrac{26}{3}y^3+\dfrac{13}{3}ay^2-\dfrac{14}{3}y^3= \\ \\ & = \boxed{9a^3+10a^2y+6ay^2+4y^3}=A(a)\end{align} \]
Il resto e il quoziente calcolati sono dunque anche in questo caso corretti.
Stessi polinomi ma differenti quoziente e resto?
Potrebbe stupire il fatto di aver ottenuto due differenti valori di quoziente e resto nelle precedenti divisioni. Infatti, abbiamo diviso tra loro in ciascuna divisione gli stessi polinomi, per cui ci aspetteremmo lo stesso risultato.
Effettivamente, il risultato della divisione tra i polinomi è lo stesso in entrambi i casi.. solo è differente il modo nel quale lo abbiamo espresso.
Come è chiaro infatti dalle due verifiche eseguite, entrambe le coppie quoziente e resto calcolate restituiscono grazie alla relazione \( A(x) = Q(x)\cdot B(x)+R(x) \) lo stesso polinomio (abbiamo qui usato la lettera \( x \) per esprimerci in modo generale).
Se infine consideriamo la relazione che abbiamo visto nella scorsa lezione:
\[ \dfrac{A(x)}{B(x)}=Q(x)+\dfrac{R(x)}{B(x)} \]
e la utilizziamo separatamente con i polinomi ordinati rispetto a ciascuna lettera e i rispettivi quozienti e resto, potremo riscrivere l’uguaglianza:
\[ \dfrac{A(y)}{B(y)}=\dfrac{A(a)}{B(a)} \]
come:
\[ Q(y)+\dfrac{R(y)}{B(y)}=Q(a)+\dfrac{R(a)}{B(a)} \]
e tale relazione sostituendo i quozienti e i resti ottenuti risulterà vera.
In altre parole, a partire da ciascuna coppia quoziente e resto si ottiene la stessa frazione algebrica. E ciò conferma quanto era logico aspettarsi: se espresso come frazione algebrica, il risultato delle due divisioni è lo stesso. 😉
Questa lezione sulla divisione tra polinomi con più lettere termina qui. Se volete esercitarvi su quanto appreso: esercizi sulla divisione tra polinomi.
Nella prossima lezione vedremo il teorema del resto.
Ciao a tutti e buono studio con Altramatica! 🙂
