Con questi esercizi avremo modo anzitutto di rivedere la regola della divisione tra polinomi, a partire da polinomi con una sola lettera. Inoltre, mostreremo come usare la regola della divisione tra polinomi con più lettere in casi del tutto generali.
Cominciamo allora subito gli esercizi sulla divisione tra polinomi a partire da un paio di esercizi con polinomi in una sola lettera (variabile).
Esercizi sulla divisione tra polinomi
Prima parte: divisione tra polinomi nel caso in cui sia presente una sola lettera
Esercizio 1 (con spiegazione passo passo sulla divisione tra polinomi)
\[ (3x^3-7x^2+1):(x-2) \]
Ripassiamo le prime definizioni. Il polinomio \( 3x^3-7x^2+1 \) è il polinomio dividendo, mentre \( x-2 \) è il polinomio divisore.
Ricordiamo le prime operazioni da fare come preparazione per la divisione:
- ordinare i polinomi rispetto alla lettera presente (o alla lettera scelta nel caso di polinomi con più lettere) per potenze decrescenti (es., \( x+2x^2-2 \) deve essere riscritto come \( 2x^2+x-2 \));
- se il polinomio dividendo non è completo rispetto alla lettera presente (o alla lettera scelta per la divisione se il polinomio contiene più lettere) dobbiamo indicare esplicitamente i coefficienti pari a zero (zeri “segnaposto”). Così ad esempio il polinomio \( 4x^3+x \) andrà riscritto come \( 4x^3+0x^2+x+0 \). Osserviamo che è necessario indicare esplicitamente anche un termine noto nullo, o al più lasciare dello spazio.
Prestiamo attenzione: i coefficienti zero e gli eventuali termini noti pari a zero vanno indicati esplicitamente soltanto nel polinomio dividendo. Invece, l’ordinamento va sempre eseguito su entrambi i polinomi dividendo e divisore.
Nel nostro caso, i polinomi sono già ordinati. Osserviamo tuttavia che il polinomio dividendo non è completo. Manca infatti il termine in \( x \). Dovremo dunque indicare esplicitamente il termine mancante attribuendo ad esso un coefficiente pari a zero:
\[ 3x^3-7x^2+0x+1 \]
Il polinomio divisore è già ordinato ed è completo.
Precisiamo che poiché il divisore è di primo grado, possiamo anche utilizzare per la divisione la regola di Ruffini. Tuttavia, eseguiremo la divisione secondo la regola generale in modo da vedere un caso semplice. 😉
Cominciamo inserendo i polinomi opportunamente preparati nella tabella della divisione:

Il primo passo è dividere il primo monomio nel dividendo per il primo monomio nel divisore:

Ora: moltiplichiamo l’ultimo termine scritto per ciascun termine del divisore. Otterremo due prodotti. Per ciascun prodotto dovremo cambiarne il segno e incolonnarlo con il rispettivo termine simile nel dividendo:

Tiriamo una linea orizzontale come a sottolineare gli ultimi termini scritti. Quindi, sommiamo algebricamente in colonna i termini del polinomio dividendo e i termini sottostanti. Gli spazi vuoti vanno considerati come termini nulli. Abbiamo:

Il polinomio \( -x^2+1 \) appena scritto rappresenta il primo resto parziale. Ora dobbiamo trattare il resto parziale stesso come se fosse il dividendo, ripetendo tutto quanto fatto finora. Quindi, dividiamo il primo monomio del resto parziale con il primo monomio del divisore:

Ancora, moltiplichiamo l’ultimo termine scritto per ciascun termine del divisore, invertendo i segni dei prodotti ottenuti. Incolonniamo questi ultimi sotto ai termini simili del resto parziale ed eseguiamo la somma algebrica tra i termini in colonna. Si ha quindi:

Ricordiamo che la divisione termina quando il grado dell’ultimo resto parziale ottenuto è minore del grado del divisore. Poiché il grado del resto parziale \( -2x+1 \) è uguale a quello del polinomio divisore, ripetiamo ancora la procedura eseguita. Abbiamo:
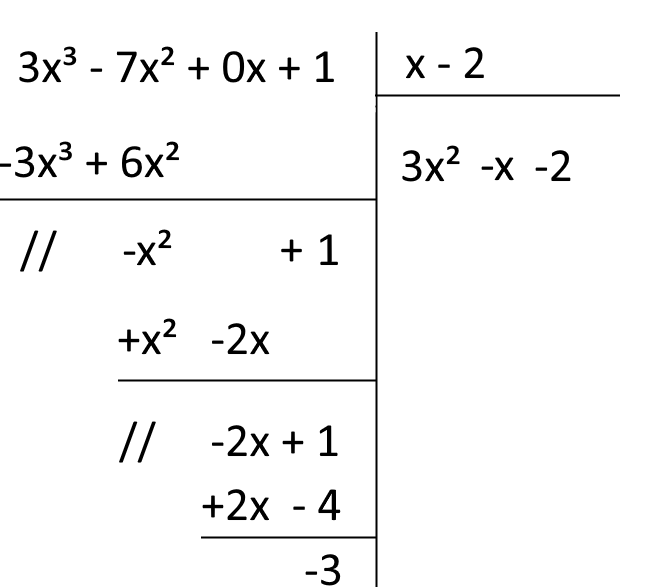
In conclusione, abbiamo ottenuto un quoziente pari a \( 3x^2-x-2 \) e un resto pari a \( -3 \). Scriveremo quindi formalmente:
\[ Q(x) = 3x^2-x-2; \qquad R(x)=-3 \]
Esercizio 2
\[ (-3x+4x^2+6):(x+2) \]
I polinomi sono completi. Sono ordinati? Il divisore sì, ma il dividendo no. Riscriviamo dunque il dividendo come:
\[ 4x^2-3x+6 \]
Ora possiamo eseguire la divisione, in modo del tutto simile all’esercizio precedente:

Abbiamo così:
\[ Q(x)=4x-11; \qquad R(x) = 28 \]
Esercizio 3
\[ \left(\dfrac{3}{2}t^5-3t^4-t^2+\dfrac{5}{2}t+2 \right):\left(\dfrac{1}{2}t-1 \right) \]
Entrambi i polinomi sono già ordinati. Tuttavia, il dividendo non è completo. Dovremo allora aggiungere uno “zero segnaposto”. Di conseguenza scriveremo il dividendo come segue:
\[ \dfrac{3}{2}t^5-3t^4+0-t^2+\dfrac{5}{2}t+2 \]
Per brevità abbiamo qui scritto semplicemente \( 0 \) invece di \( 0t^3 \).
Il polinomio divisore è invece già ordinato.
La differenza rispetto ai precedenti esercizi è data dal fatto che ora abbiamo coefficienti frazionari nei monomi. Poco male ;). Basterà ricordare la regole relative alla moltiplicazione a alla somma di frazioni. Se serve, è conveniente riprendere un po’ di allenamento con queste operazioni, così da poter eseguire a mente i prodotti e le somme tra i coefficienti frazionari dei monomi. 😉
Per il resto, anche questa divisione tra polinomi non differisce nel metodo dalle precedenti:

Otteniamo così in conclusione:
\[ Q(t)=3t^4-2t+1; \qquad R(t)=3 \]
Seconda parte: polinomi con più lettere
Esercizio 4
Eseguire la divisione tra polinomi con più lettere:
\[ (2p^3+3p^2q-6pq^2-9q^3):(p^2-3q^2) \]
Ci ritroviamo ora con dei polinomi aventi due lettere. Come ci comportiamo in questo caso?
La regola da seguire è quella di ordinare i polinomi secondo una delle due lettere presenti. Ad esempio, scegliamo di ordinare entrambi i polinomi dividendo e divisore rispetto alla lettera \( p \). Possiamo utilizzare per la lettera scelta le definizione di lettera dominante. Così, la lettera \( q \) non dovrà portarci in confusione: per la scelta fatta, essa non conta per l’ordinamento dei polinomi. Ci limiteremo a trattare la lettera \( q \) come parte dei coefficienti dei monomi in \( p \).
Osserviamo che il polinomio dividendo, ovvero \( 2p^3+3p^2q-6pq^2-9q^3 \) è già ordinato rispetto alla lettera \( p \). E attenzione, il termine noto non è zero, ma è dato dal termine \( -9q^3 \). Infatti, detto termine non contiene la lettera dominante, e concettualmente va quindi considerato come un numero. 😉 Così, scriveremo il polinomio dividendo così come è.
Il polinomio divisore è già ordinato rispetto alla lettera \( p \). Ricordiamoci inoltre che il polinomio divisore può benissimo essere incompleto. Non c’è nessun bisogno di aggiungere zeri “segnaposto”. Così, possiamo utilizzare per la divisione il polinomio divisore così come è:
\[ p^2-3q^2 \]
Ora abbiamo preparato i polinomi e possiamo eseguire la divisione. Ricordiamo che possiamo eseguire i calcoli normalmente, senza preoccuparci che la lettera dominante è la \( p \). Procediamo. 😉

Abbiamo così ottenuto il quoziente:
\[ Q(p)=2p+3q \]
e resto zero. Ricordiamo che quando la divisione tra polinomi con più lettere restituisce un resto pari a zero, non è necessario eseguire la divisione considerando come dominante l’altra lettera. Infatti, otterremmo comunque lo stesso quoziente e ancora resto zero. 😉
Per cui in conclusione diciamo che la divisione di partenza è esatta e i due polinomi sono divisibili.
Esercizio 5
Vediamo ora una divisione tra due polinomi con più lettere non esatta.
\[ \left( \dfrac{1}{2}a^6+a^5b-2a^3b^3+b^6\right):(a^4+a^2b^2-2b^4) \]
Prima di tutto, se il testo dell’esercizio non dà indicazioni in merito dobbiamo scegliere una lettera rispetto alla quale eseguire le divisioni (lettera dominante). Scegliamo ad esempio la lettera \( a \). Dovremo quindi ordinare i polinomi rispetto a questa lettera, considerando il termine o in generale i termini che non la contengono come un termine noto.
Cominciamo a preparare i polinomi, a partire dal dividendo. Osserviamo che quest’ultimo è già ordinato rispetto alla lettera \( a \), però non è completo. Mancano infatti i termini in \( a^4 \), \( a^2 \) ed \( a \). Ricordiamoci dunque gli zeri “segnaposto”. 😉
Il polinomio divisore è anch’esso già ordinato rispetto alla lettera \( a \) e, in quanto divisore, anche se incompleto non richiede gli zeri “segnaposto”.
Procediamo allora con la divisione rispetto alla lettera \( a \):

Otteniamo così il quoziente:
\[ Q(a)=\dfrac{1}{2}a^2+ab-\dfrac{1}{2}b^2 \]
e il resto:
\[ R(a)=-3a^3b^3+\dfrac{3}{2}a^2b^4+2ab^5 \]
Poiché il resto è diverso da zero, la divisione non è esatta. Per cui, in base a quanto detto nella lezione sulla divisione tra polinomi con due lettere, eseguendo la divisione rispetto all’altra lettera otterremo un quoziente e un resto differenti.
Vediamo allora cosa succede ordinando i polinomi stavolta rispetto alla lettera \( b \).
Per prima cosa, ordiniamo il polinomio dividendo rispetto alla lettera \( b \) stessa:
\[ b^6-2a^3b^3+a^5b+\dfrac{1}{2}a^6 \]
Mancano i termini in \( b^5 \), \( b^4 \) e \( b^2 \): ricordiamoci di indicarli con coefficiente zero. Il termine noto è presente, ed è dato da \( \dfrac{1}{2}a^6 \). In esso infatti non abbiamo la lettera \( b \).
Così, nella divisione scriveremo il polinomio dividendo come:
\[ b^6+0b^5+0b^4-2a^3b^3+0b^2+a^5b+\dfrac{1}{2}a^6 \]
Passiamo ora al polinomio divisore. Dobbiamo ordinarlo rispetto alla lettera \( b \), scrivendolo come segue:
\[ -2b^4+a^2b^2+a^4 \]
Ora siamo pronti per la divisione:

Otteniamo così un quoziente pari a:
\[ Q(b)=-\dfrac{1}{2}b^2-\dfrac{1}{4}a^2 \]
e un resto:
\[ P(b)=-2a^3b^3+\dfrac{3}{4}a^4b^2+a^5b+\dfrac{3}{4}a^6 \]
Ed effettivamente, poiché la divisione non è esatta abbiamo \( Q(a) \neq Q(b) \) e \( P(a) \neq P(b) \). Tuttavia, le divisioni riguardano gli stessi polinomi dividendo e divisore, soltanto ordinati con una lettera dominante differente. Ma non abbiamo nessuna contraddizione. Infatti, detti \( A(a,b) \) e \( B(a,b) \) i due polinomi dividendo e divisore di partenza, entrambe le espressioni:
\[ Q(a)+\dfrac{R(a)}{B(a)} \]
e
\[ Q(b)+\dfrac{R(b)}{B(b)} \]
saranno uguali alla frazione algebrica:
\[ \dfrac{A(a,b)}{B(a,b)} \]
che rappresenta proprio la divisione di partenza. 😉
Vediamo ora l’ultimo di questa serie di esercizi sulla divisione tra polinomi, che rappresenta il caso più generale.
Esercizio 6
\[ (a^3c+a+a^3c^2+a^2+a^2c^2+ac+3a^2c):(a+ac+1) \]
Scegliamo di ordinare i polinomi rispetto alla lettera \( a \), che sarà quindi la lettera dominante.
L’esercizio presenta delle differenze rispetto ai precedenti che abbiamo svolto. Infatti, sia nel polinomio dividendo, sia nel polinomio divisore, abbiamo dei termini che sono dello stesso grado rispetto alla lettera dominante e allo stesso tempo non sono tra loro simili. In parole più semplici, abbiamo termini tra loro non simili nei quali la lettera dominante compare con lo stesso esponente.
Poiché i termini non sono simili, non possiamo ovviamente risolvere il problema sommandoli tra loro. La domanda allora è chiara: con quale criterio ordiniamo i polinomi?
Partiamo dal polinomio dividendo. Questo ha per cominciare due termini entrambi di terzo grado rispetto alla lettera \( a \) :
\[ a^3c, \quad a^3c^2 \]
L’idea è quella di ordinare questi termini rispetto alla lettera \( c \). In un certo senso, scegliamo di utilizzare la lettera \( c \) come “dominante di secondo livello”. Ordineremo così i termini ove la lettera dominante compare con lo stesso esponente rispetto alla “vice-dominante” scelta. E attenzione, una volta scelta la “vice-dominante”, questa dovrà essere utilizzata, se necessario, anche nel polinomio divisore. Ciò significa che se anche nel divisore ci ritroviamo con dei termini tra loro non simili ma nei quali la lettera dominante compare con lo stesso esponente, dovremo ordinarli ancora utilizzando la lettera \( c \).
Così, ordineremo il polinomio dividendo come segue:
\[ \overbrace{\boxed{a^3\mathbf{c^2}+a^3\mathbf{c^1}}}^{a^3}\overbrace{\boxed{+a^2\mathbf{c^2}+3a^2\mathbf{c^1}+a^2\mathbf{c^0}}}^{a^2}\overbrace{\boxed{+a\mathbf{c^1}+a\mathbf{c^0}}}^{a} \]
ovvero:
\[ a^3c^2+a^3c+a^2c^2+3a^2c+a^2+ac+a \]
Come evidenziato graficamente, i termini in cui la lettera \( a \) compare con lo stesso esponente sono tutti ordinati rispetto alla lettera \( c \). Abbiamo così ordinato il polinomio dividendo.
Ripetiamo lo stesso ragionamento per il polinomio divisore:
\[ a\mathbf{c}+(a+1)\mathbf{c^0} \]
ovvero semplicemente:
\[ ac+a+1 \]
Osserviamo infine che entrambi i polinomi risultano completi rispetto alla lettera \( a \). Procediamo allora con la divisione:
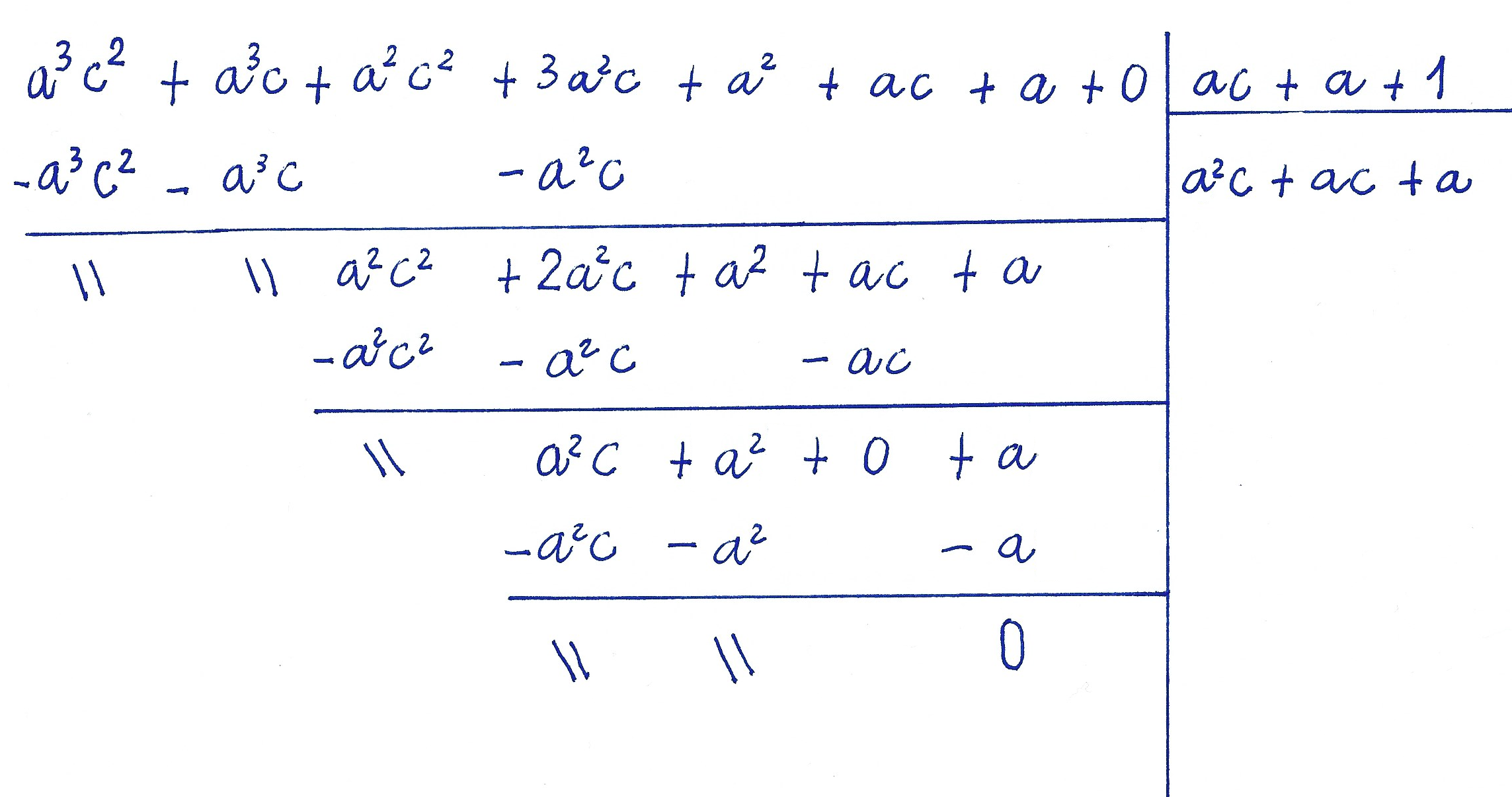
Abbiamo ottenuto un resto zero. La divisione allora è esatta ed ha come risultato il quoziente intero \( a^2c+ac+a \).
Qui terminano gli esercizi sulla divisione tra polinomi con una o più lettere. Con l’esercizio 6 abbiamo ampliato quanto esposto nella lezione sulla divisione tra polinomi con più lettere affrontando un caso particolare.
Per gli esercizi sulla divisione tra polinomi con una sola lettera, ricordo il tool: divisione tra polinomi online.
Per quanto riguarda gli esercizi sulla divisione tra polinomi è tutto! Buon proseguimento con Altramatica! 🙂
