La divisione con la regola di Ruffini presenta un procedimento molto più rapido rispetto alla generica divisione tra polinomi. Tuttavia, la regola può essere utilizzata soltanto sotto le ipotesi del teorema del resto. Ovvero, il divisore deve essere un binomio nella forma \( x-c \).
Così, per eseguire la divisione \( P(x):(x-c) \) con la regola di Ruffini dovremo costruire una semplice tabella, nella quale inseriremo come dati di partenza i coefficienti del polinomio dividendo \( P(x) \) e il valore \( c \). La tabella offrirà come risultato i coefficienti del polinomio quoziente e il resto.
Vediamo allora subito come eseguire la divisione tra polinomi con la regola di Ruffini. 🙂
NOTA: su Altramatica è anche disponibile il pratico tool divisione tra polinomi con la regola di Ruffini online. 😉
Divisione con la regola di Ruffini: un esempio pratico
Supponiamo di dover eseguire la divisione:
\[ (x^3-5x^2+8):(x-3) \]
La divisione ha effettivamente come dividendo un polinomio \( P(x) \) e come divisore un binomio di primo grado che si presenta nella forma \( x-c \), con \( c=3 \).
Costruiamo una particolare tabella, tracciando una linea orizzontale e due linee verticali come segue:

Come si può vedere la linea orizzontale non passa per la metà delle linee verticali ma è più in basso. Ciò viene fatto perché al di sopra della linea orizzontale dovremo scrivere due file di numeri. Invece, al di sotto della linea orizzontale scriveremo un’unica fila di numeri. Essa conterrà, ordinatamente, i coefficienti del polinomio quoziente e il resto della divisione.
Per comodità possiamo dunque vedere la tabella come segue. Nella pratica, comunque, la linea azzurra non viene mai tracciata.

Nella prima riga, scriviamo i coefficienti del polinomio dividendo. Prima di tutto, osserviamo però come è fatto il polinomio dividendo:
\[ x^3-5x^2+8 \]
Come possiamo vedere il polinomio non è completo in quanto manca il termine in \( x \). Il termine in \( x \) in realtà “c’è ma non si vede”: ha infatti coefficiente zero.
Nella tabella della regola di Ruffini è obbligatorio indicare anche i coefficienti pari a zero del polinomio dividendo.
Inoltre, i coefficienti devono essere scritti rigorosamente per potenze decrescenti dei termini in \( x \). Quindi, il polinomio dividendo deve essere ordinato.
Nel nostro caso il polinomio dividendo è già ordinato. Si tratta solo di indicare esplicitamente il coefficiente zero del termine in \( x \). E’ inoltre opportuno indicare esplicitamente anche i coefficienti pari a \( 1 \). Scriveremo dunque il polinomio dividendo come segue:
\[ 1x^3-5x^2+0x+8 \]
e riporteremo nella tabella i suoi coefficienti, ordinatamente, come segue:
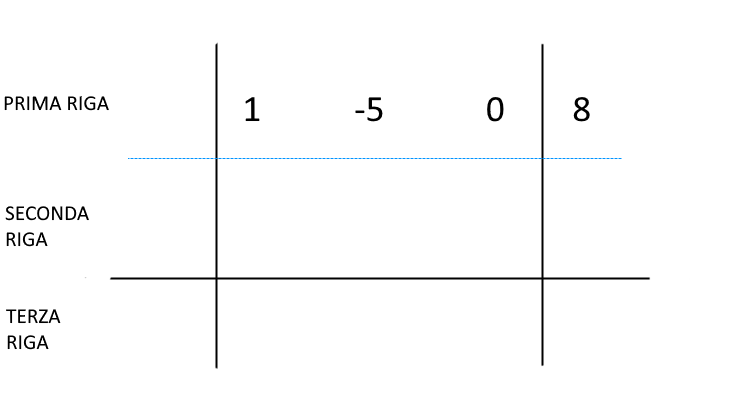
Osserviamo che abbiamo scritto i coefficienti a cominciare dalla prima posizione disponibile a destra della prima linea verticale.
Ora, nella seconda riga, a sinistra della prima linea verticale, scriviamo il numero \( c \), che nel nostro caso è pari a \( 3 \):

A questo punto, scriviamo nella terza riga, ancora a sinistra della prima linea verticale, il primo coefficiente del polinomio dividendo. La freccia indica chiaramente il coefficiente da scrivere:
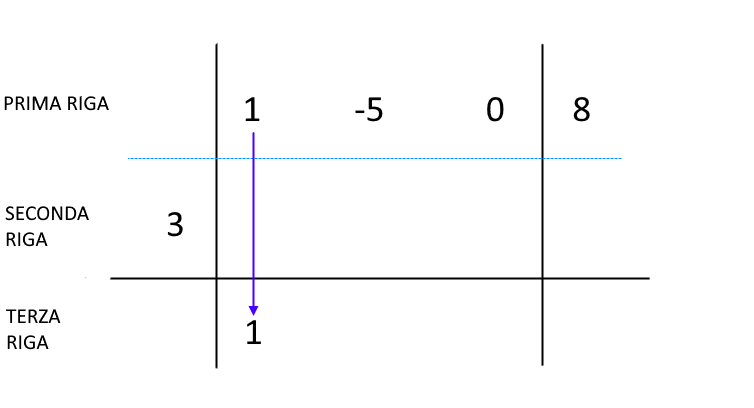
Ora moltiplichiamo il numero \( c \) per il numero appena scritto. Eseguiamo così la moltiplicazione \(3 \cdot 1 = 3 \). Scriviamo il risultato nella seconda riga, proprio sotto al secondo coefficiente del polinomio dividendo:

Adesso, eseguiamo la somma algebrica tra il secondo coefficiente del polinomio dividendo e il numero appena scritto, ovvero tra \( -5 \) e \( 3 \), scrivendo il risultato in colonna, nella terza riga:

Ora, moltiplichiamo ancora il numero \( c \) per l’ultimo numero scritto, ovvero \( -2 \). Dobbiamo quindi eseguire la moltiplicazione \( 3 \cdot (-2) =-6 \). Scriviamo il risultato ottenuto nel primo posto libero della seconda riga, ovvero sotto al penultimo coefficiente del polinomio dividendo:

Ancora, eseguiamo una somma algebrica in colonna, stavolta tra i termini \( 0 \) e \( -6 \). Scriviamo il risultato nella stessa colonna, nella terza riga:

A questo punto, in modo del tutto simile a quanto fatto in precedenza, moltiplichiamo il numero \( c \) per l’ultimo numero scritto. Effettuiamo così la moltiplicazione \(3 \cdot -6 = -18 \). Scriviamo il risultato ottenuto sotto all’ultimo coefficiente del polinomio dividendo, nella seconda riga:

Siamo arrivati. 🙂 Ora come intuibile dobbiamo sommare algebricamente in colonna i termini \( 8 \) e \( -18 \), scrivendo nell’ultimo posto rimanente il risultato ottenuto:

La costruzione della tabella è così conclusa. Quello che ci interessa è la terza riga. In essa abbiamo, ordinatamente, i coefficienti del polinomio quoziente (ordinati per potenze decrescenti) e il resto.

Siamo così arrivati a poter scrivere il risultato della divisione \( (x^3-5x^2+8):(x-3) \). Cominciamo con il quoziente.
Poiché il polinomio dividendo \( P(x) \) è di terzo grado e il polinomio divisore è di primo grado, il quoziente sarà di grado \( 3-1=2 \). Così, la terza riga ci dice che \( 1 \) è il coefficiente del termine in \( x^2 \) del polinomio quoziente, \( -2 \) è il coefficiente del termine in \( x \) e infine \( -6 \) è il termine noto sempre del polinomio quoziente.
Il polinomio quoziente è allora:
\[ Q(x)= x^2 – 2x – 6\]
Il resto della divisione è infine \( R(x) = -10 \), cioè l’ultimo numero della terza riga.
Eseguendo la divisione secondo il metodo generico, il risultato viene confermato:

Per questa lezione sulla divisione con la regola di Ruffini è tutto. 🙂 Così si conclude anche il ciclo di lezioni relative alle operazioni tra polinomi.
Nella prossima lezione, concluderemo la teoria sui polinomi con il principio di identità dei polinomi.
Dalla successiva lezione ci occuperemo invece della scomposizione dei polinomi.
Vi ricordo infine il pratico tool: divisione tra polinomi con la regola di Ruffini online.
Un saluto a tutti voi da Altramatica! 🙂
