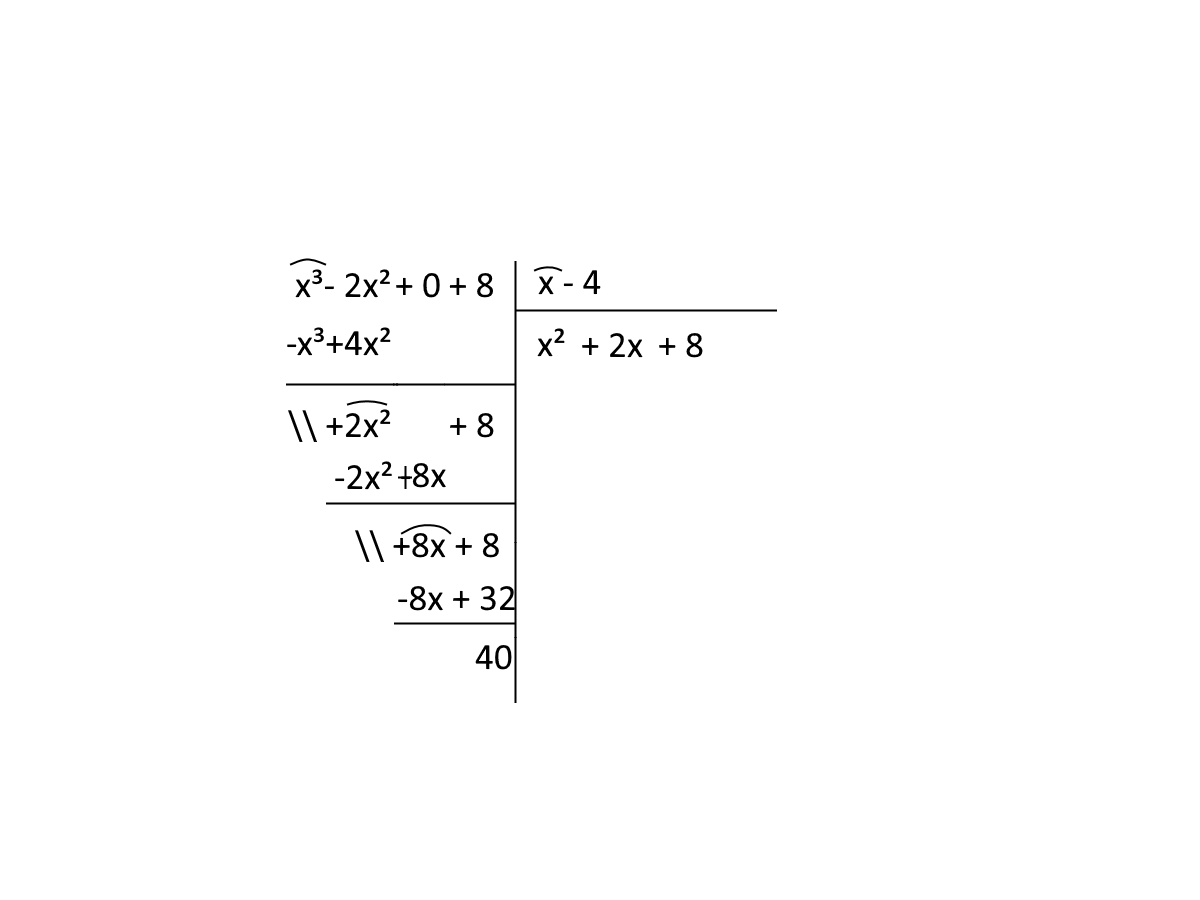Ciò che rende interessante il teorema del resto è il fatto di permettere, sotto certe ipotesi, di calcolare il resto di una divisione tra polinomi senza dover nemmeno eseguirla.
Vediamo allora subito di introdurre il teorema del resto, mostrando degli esempi pratici sul suo utilizzo. 🙂
Un nuovo criterio di divisibilità
Per quanto visto sulla divisione tra polinomi, sappiamo che un polinomio \( A(x) \) è divisibile per un polinomio \( B(x) \) se il resto della divisione \( A(x):B(x) \) è zero.
L’unico modo che abbiamo al momento per sapere se il resto è zero è quello di eseguire la divisione.
Il teorema del resto ci evita di dover eseguire la divisione tra i polinomi poiché ci consente di calcolare il resto della divisione senza dover eseguirla. Tuttavia, il teorema può essere utilizzato soltanto per calcolare il resto di una divisione tra un polinomio qualsiasi e uno di primo grado (quest’ultimo è il divisore).
Già sappiamo che il resto di una divisione tra polinomi è sempre di grado inferiore al polinomio divisore. Così, assegnata la divisione tra polinomi:
\[ A(x):B(x) \]
il grado del resto \( R(x) \) sarà sempre minore del grado del polinomio divisore \( B(x) \).
In generale non possiamo sapere quanto sarà esattamente il grado del resto. Infatti, se ad esempio \(B(x) \) è un polinomio di secondo grado, il resto potrà essere di primo grado oppure di grado zero (cioè un numero).
Vi è però un caso particolare nel quale possiamo prevedere con sicurezza che grado avrà il resto della divisione. Questo è il caso nel quale il polinomio divisore \( B(x) \) è di primo grado. In tale circostanza, il resto non potrà essere che di grado zero, ovvero il resto sarà un numero.
Il teorema del resto va oltre la considerazione fatta, poiché ci permette addirittura di prevedere con esattezza quanto sarà il resto senza nemmeno dover eseguire la divisione.
Teorema del resto
Sia assegnata la divisione:
\[ P(x) : (x-c) \]
ovvero la divisione tra un generico polinomio \( P(x) \) e il polinomio (di primo grado) \( x-c \).
Il resto della divisione è allora dato da:
\[ P(c) \]
ovvero dalla valutazione del polinomio \( P(x) \) per \( x = c \).
Questo è l’enunciato del teorema. Ora, c’è un’importante considerazione da fare. Nel caso particolare in cui il polinomio \( P(x) \) sia divisibile per il polinomio \( x-c \), allora il resto della divisione \( P(x):(x-c) \) sarà per forza zero. E poiché come afferma il teorema del resto, il valore del resto si ottiene tramite la valutazione \( P(c) \), mettendo insieme quanto detto otteniamo il seguente teorema, noto come teorema di Ruffini.
Teorema di Ruffini
“Se \( P(c)=0 \), allora il polinomio \( P(x) \) è divisibile per il polinomio \( x-c \).”
La dimostrazione del teorema di Ruffini è immediata e praticamente l’abbiamo già fatta introducendo il teorema stesso ;). In ogni caso, la tesi del teorema di Ruffini discende immediatamente dal fatto che per il teorema del resto \( P(c) \) è il resto della divisione, e se il resto è zero i due polinomi sono divisibili.
Il teorema di Ruffini costituisce un agevole criterio di divisibilità tra un polinomio e un binomio di primo grado. Infatti, per determinare se \( P(x) \) è divisibile per il binomio \( x-c \) è sufficiente calcolare \( P(c) \) e controllare se è zero. Pratico no?
Esempi sul teorema del resto e il teorema di Ruffini
Esempio 1
Determinare se il polinomio \( x^2-5x+6 \) è divisibile per il binomio \( x-2 \).
Poiché il polinomio \( x-c \) è in questo caso \( x-2 \), abbiamo che \( c=2 \). Calcoliamo allora il valore del polinomio \( x^2-5x+6 \) per \( x=2 \):
\[ P(2)=2^2-5 \cdot 2 +6= 0 \]
Poiché la valutazione del polinomio in \( x=c \) è nulla, per il teorema di Ruffini il polinomio \( x^2-5x+6 \) è divisibile per il polinomio \( x-2 \).
Esempio 2
Determinare il resto della divisione:
\[ (x^3-2x^2+8):(x-4) \]
Osserviamo che il binomio \( x-c \) è in questo caso \( x-4 \) per cui si ha \( c = 4 \).
Per il teorema del resto, il resto della divisione è dato da:
\[ P(4)=(4)^3-2 \cdot (4)^2+8= 64-32+8=40\]
ed infatti eseguendo la divisione:
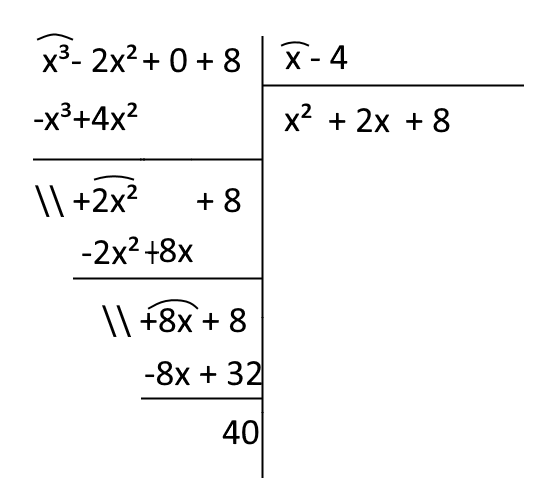
otteniamo proprio un resto pari a \( 40 \). 😉
Esempio 3
Determinare il resto della divisione:
\[ (x^2-8):(x+5) \]
Poiché il binomio \( x-c \) è in questo caso \( x + 5 \), si ha \( c=-5 \). In caso di dubbi nel segno, è consigliabile provare a sostituire il valore di \( c \) che abbiamo trovato nel binomio in forma generica \( x-c \). Effettivamente ponendo \( c = -5 \) abbiamo:
\[ x-c \quad \Rightarrow \quad x-(-5)=x+5 \]
e ritroviamo così, correttamente, il binomio divisore. 😉
Per il teorema del resto, otteniamo:
\[ P(-5)=(-5)^2-8=25-8=17 \]
Vediamo la divisione:
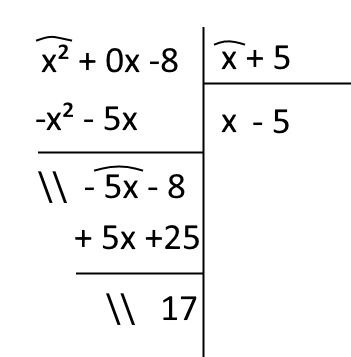
Effettivamente otteniamo un resto pari a \( 17 \).
Concludiamo ora la lezione fornendo la dimostrazione del teorema del resto.
Dimostrazione del teorema del resto
Ricordiamo l’enunciato del teorema del resto:
“Il resto della divisione \( P(x):(x-c) \) è pari a \( P(c) \)”.
Per quanto noto sulla divisione, possiamo scrivere per il nostro caso:
\[ P(x)=Q(x) \cdot (x-c) + R\]
Infatti, il dividendo si ottiene sommando al prodotto del quoziente per il divisore il resto.
Nel nostro caso ricordiamo che \( R \) è un numero poiché il divisore è di primo grado. Per cui \( R \) non dipende da \( x \) e non dobbiamo indicare il resto con \( R(x) \).
Poiché vogliamo mostrare che la valutazione \( P(c) \) deve fornire il resto della divisione, proviamo a porre \( x = c \) nella precedente relazione e vediamo cosa succede. Si ha:
\[ P(c)=Q(c) \cdot (c-c) + R \]
e poiché evidentemente \( c-c=0 \) si ottiene in conclusione:
\[ P(c) = R \]
Il teorema del resto è così dimostrato.
Per questa lezione sul teorema del resto è tutto. Nella prossima lezione vedremo la regola di Ruffini per eseguire la divisione tra un generico polinomio e un binomio di primo grado.
Un saluto a tutti voi! 🙂