La classificazione delle frazioni in frazioni proprie, improprie ed apparenti non è affatto difficile ma richiede soltanto di comprendere e al tempo stesso memorizzare alcune definizioni.
In particolare, vedremo come riconoscere le frazioni proprie, improprie o apparenti non solo introducendo le definizioni, ma anche presentando degli esempi pratici. E’ inoltre disponibile anche un’esercitazione sulle frazioni proprie, improprie e apparenti, della quale forniremo il link alla fine della lezione. 😉
Cominciamo allora subito a capire cosa sono le frazioni proprie, improprie ed apparenti e come distinguerle tra loro. 😉
Frazioni proprie
Una frazione si dice propria se il numeratore è minore del denominatore.
Così, le frazioni:
\[ \dfrac{1}{2}; \quad \dfrac{3}{4}; \quad \dfrac{7}{9} \]
sono tutte frazioni proprie.
Osserviamo che poiché nelle frazioni proprie il numeratore è sempre minore del denominatore, una qualsiasi frazione propria rappresenta una quantità sempre minore di \( 1 \).
Possiamo rappresentare graficamente le frazioni appena scritte, e vedremo che per ciascuna di esse avanzerà sempre qualcosa della ormai onnipresente torta (la quale rappresenta, ricordiamo, l’unità):

Frazioni improprie ed apparenti
Le frazioni improprie e le frazioni apparenti rappresentano altre importanti classificazioni delle frazioni numeriche.
Una frazione sarà sicuramente impropria oppure apparente se il numeratore è maggiore del denominatore. Tuttavia, per una frazione essere impropria vuol dire una cosa, essere apparente vuol dire un’altra 😉
Capiamo quindi che se in una frazione il numeratore è maggiore del denominatore possiamo sicuramente escludere che la frazione sia propria, ma non sappiamo se questa è impropria o apparente. Abbiamo quindi bisogno di ulteriori definizioni per meglio capire queste proprietà. In questo modo, capiremo anche cosa succede quando numeratore e denominatore sono uguali.
Frazioni apparenti
Una frazione si dice apparente se il numeratore è maggiore del denominatore e se il numeratore è divisibile per il denominatore.
Inoltre, una frazione è apparente se il numeratore e il denominatore sono uguali.
In altre parole, una frazione si dice apparente se equivale ad un numero intero. In un certo senso, una frazione apparente è un “numero intero mascherato da frazione”. Infatti, una frazione apparente rappresenta una divisione che ha come risultato un quoziente intero con resto zero.
Dalle due definizioni date capiamo subito due cose:
- in presenza di una frazione con numeratore maggiore del denominatore, questa è apparente solo se il numeratore è un multiplo (intero) del denominatore;
- se una frazione ha numeratore e denominatore uguali, questa è una frazione apparente uguale all’unità. Ad esempio, dividendo l’unità in cinque parti e prendendo cinque parti, consideriamo una quantità pari a \( 1 \).
Le frazioni:
\[ \dfrac{10}{5}; \quad \dfrac{20}{10}; \quad \dfrac{33}{3} \]
sono tutte frazioni apparenti. Infatti, in ciascuna il numeratore è divisibile per il denominatore. Così, ciascuna frazione è uguale ad un numero intero:
\[ \dfrac{10}{5}=2; \quad \dfrac{20}{10}=2; \quad \dfrac{33}{3}=11 \]
E ovviamente, sono frazioni apparenti anche le seguenti frazioni con numeratore uguale al denominatore, tutte pari all’unità:
\[ \dfrac{7}{7}=1; \quad \dfrac{5}{5}= 1 \]
Se volete, in modo sintetico possiamo affermare che una frazione è apparente se il numeratore è multiplo del denominatore o è uguale ad esso 😉
Frazioni improprie
L’ultimo caso da esaminare è quando il numeratore è maggiore del denominatore ma il numeratore non è divisibile per il denominatore. In quest’ultimo caso diciamo che la frazione è impropria.
Una frazione è quindi impropria se il numeratore è maggiore del denominatore e il numeratore non è multiplo intero del denominatore.
Ad esempio le seguenti frazioni:
\[ \dfrac{7}{6}; \quad \dfrac{4}{3}; \quad \dfrac{14}{9} \]
sono tutte frazioni improprie. Non sono apparenti poiché pur avendo il numeratore maggiore del denominatore, il numeratore non è multiplo intero del denominatore.
In altre parole, per dirla con la divisione, le frazioni improprie rappresentano operazioni di divisione fra numeri interi con dividendo (numeratore) maggiore del divisore (denominatore) e resto sempre diverso da zero.
Esempio sulle frazioni proprie, improprie e apparenti
Determinare se ciascuna delle seguenti frazioni è propria, impropria o apparente.
\[ \dfrac{3}{7}; \quad \dfrac{27}{5}; \quad \dfrac{68}{17} \]
La frazione \( \dfrac{3}{7} \) è propria. Infatti, il numeratore è più piccolo del denominatore.
La frazione \( \dfrac{27}{5} \) ha il numeratore maggiore del denominatore, e quindi potrebbe essere impropria ma anche apparente. Per decidere, dobbiamo vedere se il numeratore è divisibile per il denominatore.
Osserviamo che la divisione \( 27:5 \) ha resto. Abbiamo un quoziente pari a \( 5 \) e un resto pari a \( 27-5 \times 5 = 2 \). Di conseguenza, il numeratore oltre ad essere più grande del denominatore non è nemmeno divisibile per esso e pertanto concludiamo che la frazione \( \dfrac{27}{5} \) è impropria.
La frazione \( \dfrac{68}{17} \) ha il numeratore maggiore del denominatore. A occhio non è gran che evidente, ma abbiamo che il numeratore è divisibile per il denominatore. Eseguendo infatti la divisione, ci accorgiamo che \( 68 \) è un multiplo intero di \( 17 \). Infatti \( 68:17=4 \) con resto zero. Concludiamo dunque che la frazione \( \dfrac{68}{17} \) è apparente ed equivalente al numero \( 4 \).
Mentre le frazioni proprie sono facilmente riconoscibili, per distinguere tra frazioni improprie ed apparenti serve un po’ di attenzione. Ad esempio, ad occhio avreste detto che \( 68 \) è divisibile per \( 17 \)?
Approfondimento: perché l’uso dei termini “propria” e “impropria”? I numeri misti
Ci si potrebbe a questo punto domandare perché siano stati scelti i termini “propria” e “impropria” per indicare i rispettivi tipi di frazione.
Se da un lato è abbastanza ovvio che il termine “apparente” indichi una frazione che in realtà è esprimibile come un numero, non potrebbe essere evidente all’inizio il perché dell’uso dei termini “propria” e “impropria”.
Diciamo subito che una frazione propria non è esprimibile in alcun modo mediante l’uso dei numeri interi. Qualsiasi frazione propria con numeratore non nullo esprime una quantità minore di uno e maggiore di zero, dunque impossibile da rappresentare con un numero intero.
A sua volta anche una frazione impropria non può essere rappresentata soltanto attraverso un numero intero, tuttavia può essere riscritta in una forma particolare che utilizza anche un numero intero.
Si può infatti dimostrare che qualsiasi frazione impropria può essere espressa come somma di un numero intero e di una frazione propria.
Quindi, una frazione impropria in qualche modo contiene dentro di sé un numero intero. In un certo senso, non è quindi propriamente una frazione allo stesso modo di una frazione propria. Sono entrambe frazioni, sia chiaro, ma lo sono in un modo un po’ diverso. 😉
Esempio di frazione impropria espressa come somma di un numero intero e una frazione propria
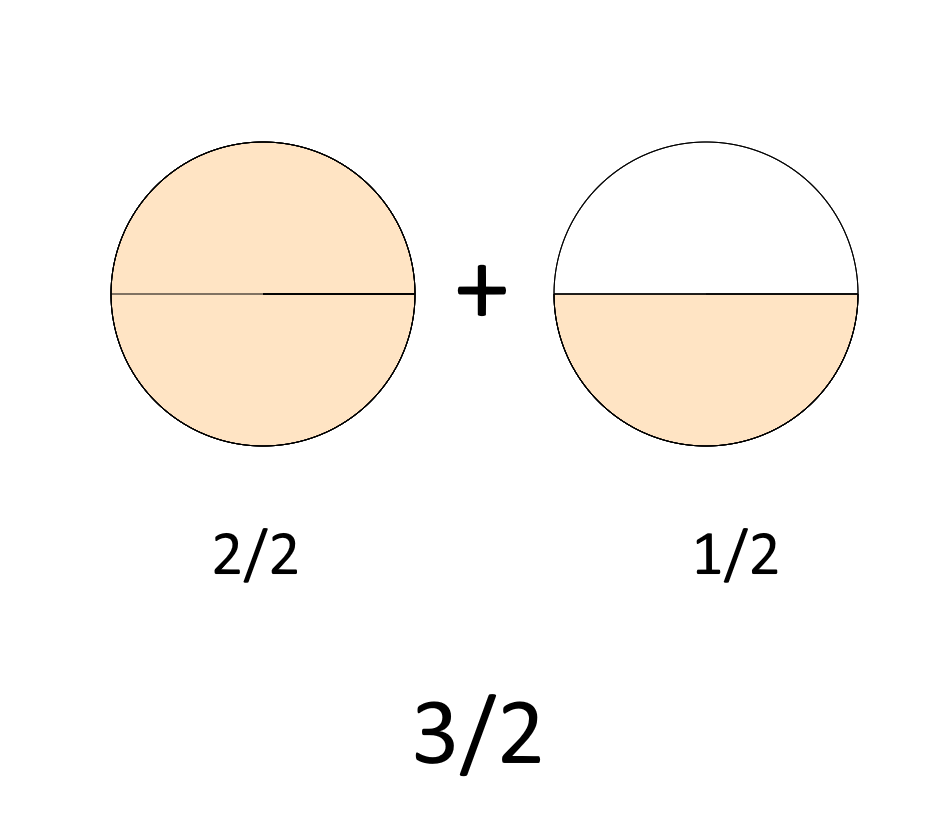
Consideriamo ad esempio la frazione \( \dfrac{3}{2} \). Si tratta di una frazione impropria poiché il numeratore è maggiore del denominatore e non è divisibile per esso.
Proviamo a rappresentare graficamente la frazione. Tiriamo fuori dal frigo l’onnipresente torta e chiediamoci: cosa vuol dire prendere \( \dfrac{3}{2} \) di una torta? Vi dico subito che se avete una sola torta nel frigo, non ci sarà verso… 😉
Tre mezzi significa prendere due pezzi da un mezzo, più un altro pezzo da un mezzo. Ma due pezzi da un mezzo… sono semplicemente una torta! Infatti \( \dfrac{2}{2}=1 \). Quindi dobbiamo prendere una torta… più un’altra mezza torta:
\[ \dfrac{2}{2}+\dfrac{1}{2}=\dfrac{3}{2} \]
e quindi:
\[ 1 + \dfrac{1}{2}= \dfrac{3}{2} \]
E così siamo arrivati. La frazione impropria \( \dfrac{3}{2} \) è esprimibile come somma di un numero intero (\( 1 \)) e di una frazione propria (\( \dfrac{1}{2} \))!
Una quantità data dalla somma di un numero intero e di una frazione propria si dice numero misto. Di conseguenza,
ogni frazione impropria è esprimibile come numero misto.
Questa lezione sulle frazioni proprie, improprie e apparenti si conclude qui. Se volete mettervi alla prova con quanto appreso, è disponibile questa esercitazione sulle frazioni proprie, improprie e apparenti.
Se vi interessa conoscere di più sulle frazioni e già avete presenti i concetti di massimo comune divisore, minimo comune multiplo e sapete come ridurre una frazione ai minimi termini, allora potete proseguire lo studio delle frazioni a partire dalla lezione sul confronto tra frazioni e successive. Diversamente nessun problema, potete semplicemente seguire le lezioni di Altramatica secondo il loro ordine. 😉
Nella prossima lezione riassumeremo la definizione di divisibilità e faremo la conoscenza dei numeri pari e dispari. Buono studio a tutti!
