Il procedimento di ridurre (semplificare) una frazione ai minimi termini richiede la conoscenza del calcolo del Massimo Comune Divisore ed è infatti una sua importante applicazione.
Nell’ultimo paragrafo vengono spiegati due metodi più pratici per semplificare le frazioni. Tuttavia, questi non sono che una versione più abbordabile del metodo che usa direttamente il Massimo Comune Divisore.
Frazione ridotta ai minimi termini
Assegnata una qualsiasi frazione è possibile scrivere infinite frazioni equivalenti ad essa. Ad esempio:
\[ \dfrac{2}{3}=\dfrac{4}{6}=\dfrac{8}{12}=\dots \]
Tutte queste frazioni si equivalgono tra loro. In altre parole, effettuando la corrispondente divisione otteniamo lo stesso identico numero decimale.
Una frazione è ridotta ai minimi termini se le scomposizioni in fattori primi del numeratore e del denominatore non presentano fattori in comune.
Ad esempio, la frazione:
\[ \dfrac{1}{2} \]
è già ridotta ai minimi termini. Infatti, il numeratore e il denominatore sono entrambi numeri primi diversi tra loro e non è possibile alcuna scomposizione.
La frazione:
\[ \dfrac{2}{6} \]
potrebbe invece non essere ridotta ai minimi termini. Infatti, il numeratore è un numero primo, ma il denominatore non lo è. Di conseguenza, è possibile scomporre il denominatore in fattori primi. In particolare abbiamo: \( 6=2 \times 3 \).
Ora, riscriviamo la frazione data utilizzando la scomposizione in fattori primi del denominatore:
\[ \dfrac{2}{6}=\dfrac{2}{2 \times 3} \]
Come possiamo vedere, il fattore \( 2 \) è in comune al denominatore e al numeratore. Osserviamo che in generale dividendo numeratore e denominatore di una frazione per uno stesso numero otteniamo una frazione equivalente a quella data. Possiamo dunque tranquillamente dividere numeratore e denominatore per il fattore primo comune \( 2 \) ottenendo:
\[ \dfrac{2}{6}=\dfrac{2:2}{(2 \times 3):2}=\dfrac{1}{3} \]
NOTA: le parentesi a denominatore sono superflue (vedi regole di precedenza delle operazioni) ma sono state inserite per maggior chiarezza.
Vediamo un altro esempio. La frazione:
\[ \dfrac{75}{28} \]
è ridotta ai minimi termini? E’ immediato osservare che sia il numeratore, sia il denominatore sono scomponibili in fattori primi ma attenzione, ciò non basta per affermare che la frazione non è ridotta ai minimi termini! Prima di poter essere sicuri di poterlo dire, dobbiamo scomporre il numeratore e il denominatore in fattori primi 😉
Abbiamo:
\[ \dfrac{75}{28}=\dfrac{3 \times 5^2}{2^2 \times 7} \]
Come possiamo vedere, non abbiamo nessun fattore primo in comune tra numeratore e denominatore. Di conseguenza, la frazione \( \dfrac{75}{28} \) è già ridotta ai minimi termini.
Riduzione di una frazione ai minimi termini e MCD
Ci domandiamo ora: che caratteristiche deve avere il numero al quale dividiamo il numeratore e il denominatore della frazione per ridurla ai minimi termini?
Sicuramente, il numero deve essere divisore sia del numeratore, sia del denominatore.
Inoltre, deve essere il più grande divisore del numeratore e del denominatore. Se così non fosse, non avremmo ridotto la frazione ai minimi termini e dovremmo ancora procedere nella sua riduzione. Noi pretendiamo di trovare, se esiste, quel divisore che ci permetta di ottenere in un colpo solo la frazione ridotta ai minimi termini 😉
Per tutte le considerazioni fatte, questo numero non può essere che il Massimo Comune Divisore (MCD) tra il numeratore e il denominatore della frazione.
Ovviamente, se ci accorgiamo che l’MCD del numeratore e del denominatore di una data frazione non esiste (nel senso che non esiste diverso da 1), vorrà dire che questa è già ridotta ai minimi termini 😉
Esempio 1
Ridurre ai minimi termini la frazione:
\[ \dfrac{126}{70} \]
Il primo passo è trovare l’\( MCD \) del numeratore e del denominatore. Scomponiamo prima di tutto i numeri in fattori primi:
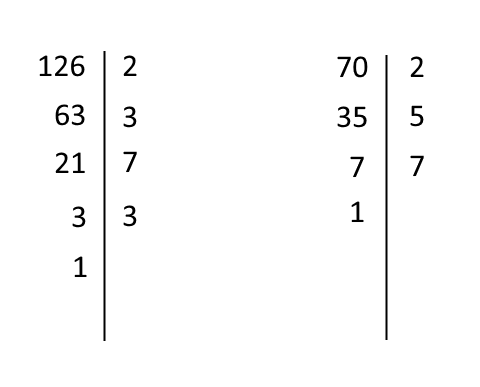
Abbiamo dunque le scomposizioni:
\[ 126=2 \times 3^2 \times 7 \]
\[ 70=2 \times 5 \times 7 \]
Determiniamo ora l’MCD del numeratore e del denominatore della frazione. I fattori primi comuni nelle scomposizioni sono \( 2 \) e \( 7 \). Il più piccolo esponente con il quale compaiono entrambi i fattori comuni è \( 1 \), per cui abbiamo:
\[ MCD(126,70)=2 \times 7 = 14 \]
E il numero ottenuto, \( 14 \), è proprio il numero con il quale dobbiamo dividere il numeratore e il denominatore della frazione assegnata:
\[ \dfrac{126}{70}=\dfrac{126:14}{70:14}=\dfrac{9}{5} \]
Dunque, la frazione \( \dfrac{126}{70} \) equivale alla frazione ridotta ai minimi termini \( \dfrac{9}{5} \).
Due metodi semplificati per ridurre le frazioni ai minimi termini
Il metodo sin qui presentato per semplificare una frazione è quello che deriva direttamente dalla teoria (in particolare, dal concetto di MCD) ma potrebbe non sempre essere la strada più facile per semplificare una frazione. Ad esempio, consideriamo la frazione:
\[ \dfrac{504}{280} \]
L’MCD del numeratore e del denominatore è:
\[ MCD(504,280)=56 \]
Ora, non è per nulla comodo dividere numeratore e denominatore della frazione per \( 56 \). Come possiamo rendere la procedura più semplice?
La prima idea è quella di scomporre in fattori primi numeratore e denominatore e riscrivere la frazione utilizzando queste scomposizioni. Abbiamo:

Quindi possiamo riscrivere la frazione come segue:
\[ \dfrac{504}{280}=\dfrac{2^3 \times 3^2 \times 7}{2^3 \times 5 \times 7}= \dfrac{\cancel{2^3} \times 3^2 \times \cancel{7}}{\cancel{2^3} \times 5 \times \cancel{7}}= \dfrac{3 \times 3}{5} \]
In generale, può essere di aiuto riscrivere queste scomposizioni come prodotto tra numeri primi senza usare le potenze:
\[ \small \dfrac{504}{280}=\dfrac{2^3 \times 3^2 \times 7}{2^3 \times 5 \times 7}=\dfrac{2 \times 2 \times 2 \times 3 \times 3 \times 7}{2 \times 2 \times 2 \times 5 \times 7}=\dfrac{\not2 \times \not2 \times \not2 \times 3 \times 3 \times \not7}{\not2 \times \not2 \times \not2 \times 5 \times \not7}=\dfrac{3 \times 3}{5} \]
In tal modo non dobbiamo usare le proprietà delle potenze e siamo più sicuri di non sbagliare. Quando si è all’inizio, si può fare. 😉
A questo punto moltiplichiamo i fattori rimasti a numeratore e denominatore ottenendo infine:
\[ \dfrac{3 \times 3}{5}=\dfrac{9}{5} \]
Quindi, la frazione data \( \dfrac{504}{280} \) ridotta ai minimi termini diventa \( \dfrac{9}{5} \).
Il secondo metodo che vi proponiamo è quello più usato e consiste nell’utilizzare delle semplificazioni fatte in sequenza. Considerando questa stessa frazione, il metodo è il seguente:
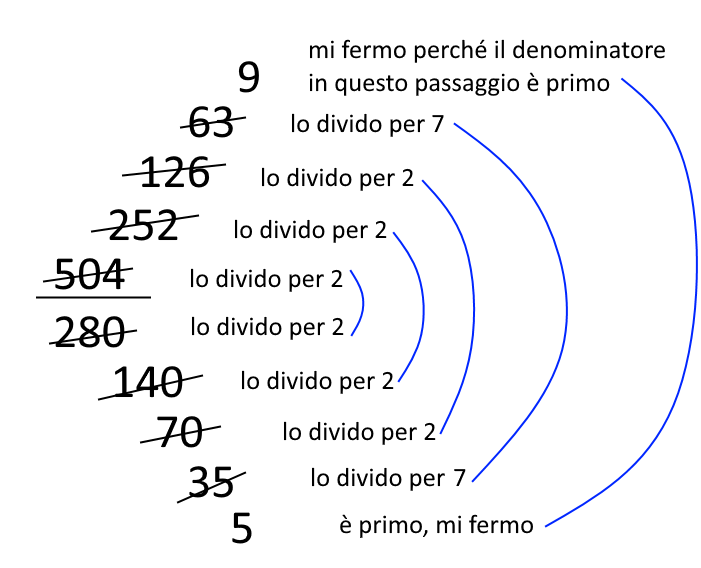
Come mostra il disegno, ogni volta dividiamo numeratore e denominatore per uno stesso numero che è divisore di entrambi. Otteniamo così ad ogni passo una frazione equivalente che viene ulteriormente semplificata fino a diventare la frazione ridotta ai minimi termini equivalente a quella data.
E’ fondamentale prestare attenzione al fatto che in ciascuna semplificazione il divisore utilizzato è lo stesso sia per numeratore, sia per denominatore. Se in uno stesso passaggio usassimo un divisore diverso per numeratore e denominatore faremmo un gravissimo errore e non otterremmo una frazione equivalente a quella data. Ricordiamo: una frazione rappresenta una divisione, e la proprietà invariantiva deve essere rispettata. Quindi, attenti! 🙂
Ci accorgiamo di essere arrivati alla fine quando numeratore e denominatore non possono essere ulteriormente divisi per uno stesso numero. Questo succede quando numeratore e denominatore non presentano tra loro fattori in comune o comunque quando almeno uno dei due tra numeratore e denominatore è primo.
Per questa lezione sul procedimento per ridurre una frazione ai minimi termini è tutto. Nella prossima lezione vedremo il minimo comune multiplo (mcm). Ciao a tutti e buono studio con Altramatica! 🙂
