Esercizio 1 (esercizi sulla scomposizione dei polinomi – quadrato di un trinomio)
Scomporre il polinomio:
\[ \frac{4}{9}a^2+\frac{9}{16}b^2+\frac{14}{3}a-\frac{21}{4}b-ab+\frac{49}{4} \]
Quando ci sono così tanti termini, è il caso di dare un’occhiata se per caso c’è qualche quadrato nei paraggi 😉 I primi due termini, guarda caso, sono i quadrati rispettivamente di \( \frac{2}{3}a \) e \( \frac{3}{4}b \). Vediamo se c’è anche il terzo quadrato, in modo da ipotizzare il quadrato di un trinomio. Ed eccolo, è in fondo: \( \frac{49}{4} \) è ovviamente il quadrato di \( \frac{7}{2} \).
Fermi lì 😉 Prima di dire che il polinomio assegnato è il quadrato di un trinomio, dobbiamo verificare i doppi prodotti. Osserviamo che questi in modulo tornano, tuttavia abbiamo due doppi prodotti che hanno segno negativo. Ora, quale segno dobbiamo attribuire ai termini \( \pm \frac{2}{3}a \), \( \pm \frac{3}{4}b \) e \( \pm \frac{7}{2} \)? Siccome due doppi prodotti sono negativi, tali termini non possono certamente essere tutti positivi.
Vediamo che il doppio prodotto tra \( \pm \frac{7}{2} \) e \(\pm \frac{2}{3}a \) è positivo, per cui questi termini saranno concordi. Il prodotto tra \( \pm \frac{3}{4}b \) e \( \pm \frac{7}{2} \) è negativo, per cui questi termini saranno discordi. Stesso discorso per il prodotto tra i termini \( \pm \frac{2}{3}a \) e \( \pm \frac{3}{4}b \), anch’esso negativo (quindi anche questi due termini sono discordi).
Attribuiamo dunque lo stesso segno ai termini che sappiamo essere concordi, ad esempio il segno più:
\[ +\frac{2}{3}a; \qquad +\frac{7}{2} \]
Ora, siccome le altre coppie di termini nei rimanenti doppi prodotti devono essere tra loro discordi, non resta che attribuire il segno meno al termine rimanente:
\[ -\frac{3}{4}b \]
Possiamo dunque scomporre il polinomio assegnato come quadrato di un trinomio:
\[ \left (\frac{2}{3}a-\frac{3}{4}b+\frac{7}{2} \right )^2 \]
Osserviamo che avremmo potuto anche attribuire segno meno ai due termini concordi e segno più al rimanente termine, ottenendo la scomposizione, anch’essa corretta:
\[ \left(-\frac{2}{3}a+\frac{3}{4}b-\frac {7}{2} \right)^2 \]
Esercizio 2 (differenza di due quadrati)
Scomporre il polinomio:
\[ \frac{4}{9}a^6c^4-\frac{9}{4}a^4c^6 \]
Il polinomio è la differenza dei quadrati dei termini, rispettivamente, \( \frac{2}{3}a^3c^2 \) e \( \frac{3}{2}a^2c^3 \). Dunque, vale la scomposizione:
\[ \frac{4}{9}a^6c^4-\frac{9}{4}a^4c^6 = \left(\frac{2}{3}a^3c^2-\frac{3}{2}a^2c^3 \right) \left(\frac{2}{3}a^3c^2+\frac{3}{2}a^2c^3 \right) \]
Esercizio 3
Scomponiamo:
\[ (x+y)^2-z^4 \]
E’ abbastanza immediato ricondurre il polinomio ad una differenza tra quadrati. Ancora una volta, il trucco consiste nell’usare le potenze di potenze, in modo da riesprimere il termine alla quarta potenza come il quadrato di un quadrato:
\[ (x+y)^2-z^4=(x+y)^2-(z^2)^2=(x+y-z^2)(x+y+z^2) \]
Come ulteriore spiegazione, consideriamo che abbiamo applicato semplicemente la formula:
\[ a^2-b^2=(a-b)(a+b) \]
ponendo, nel caso specifico:
\[ a = x+y; \qquad b = z^2 \]
Esercizio 4 (esercizi sulla scomposizione dei polinomi con la regola di Ruffini)
Scomponiamo il polinomio:
\[ 4x^4-6+x^2+x^6 \]
Non sembrano esserci altre alternative. Il polinomio deve essere scomposto con la Regola di Ruffini. Per comodità, riordiniamo i termini dal grado più alto al grado più basso:
\[ x^6+4x^4+x^2-6 \]
Osserviamo che il polinomio si annulla per \( x=1 \), per cui abbiamo una sua radice, che useremo nella tabella.
La regola di Ruffini andrà applicata due volte. Riporto direttamente le due tabelle necessarie per i calcoli. Le tabelle sono state unite, cosa che si può fare quando è necessario riapplicare la regola.
Nella seconda tabella è presente la radice -1. Infatti, il polinomio \( x^5+x^4+5x^3+5x^2+6x+6 \), risultato della prima scomposizione, si annulla per \( x = -1 \).
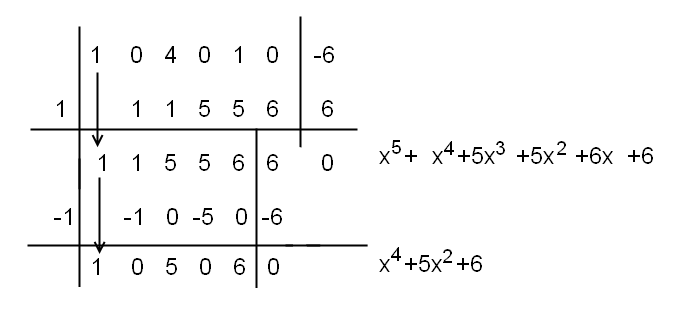
Per chi ha dubbi sulla regola di Ruffini, basta un click 😉
Grazie alla regola di Ruffini, applicata due volte, possiamo scomporre il polinomio assegnato come:
\[ x^6+4x^4+x^2-6=(x-1)(x+1)(x^4+5x^2+6)) \]
Ora, scomporre il termine \( x^4+5x^2+6 \) è possibile ma non molto immediato. E’ inutile provare a trovare una radice del polinomio. Semplicemente, non esiste alcun valore che possa annullarlo, infatti i termini \( x^4 \) e \( 5x^2 \) sono sempre positivi e il termine noto è positivo e diverso da zero. Possiamo tuttavia operare una impropriamente detta “sostituzione di variabile”. Poniamo:
\[ t=x^2\]
in questo modo, il polinomio diventa:
\[ t^2+5t+6=0 \]
Ora, questo polinomio si può scomporre in quanto è un trinomio caratteristico. Si tratta quindi di determinare i due valori \( h \) e \( k \) per i quali si potrà esprimere il trinomio come:
\[ t^2+(h+k)t+h \cdot k \]
Tali valori, da ricercare tra i divisori positivi e negativi del termine noto 6, sono \( 2 \) e \( 3 \). Il polinomio espresso in \( t \) potrà dunque scomporsi così:
\[ t^2+5t+6=(t+3)(t+2) \]
Ora, sostituendo la \( x \) alla \( t \), effettuando cioè il cambio di variabile inverso:
\[ x^2=t \]
possiamo scrivere:
\[ x^4+5x^2+6=(x^2+3)(x^2+2) \]
Di conseguenza, il polinomio da scomporre dato inizialmente potrà essere scomposto come:
\[ x^6+4x^4+x^2-6=(x-1)(x+1)(x^2+3)(x^2+2) \]
Esercizio 5
Scomponiamo il polinomio:
\[ x^6 + y^3 \]
Utilizzando le potenze di potenze, il polinomio può essere riscritto come:
\[ (x^2)^3+y^3 \]
Ci siamo così ricondotti alla somma di due potenze ad uguale esponente. Da quanto appreso nella teoria, possiamo dire che il polinomio da scomporre è divisibile per il termine \( (x^2+y) \). Ora, l’altro fattore necessario per la scomposizione si ottiene costruendo il falso quadrato a partire dai termini \( x^2 \) e \( y \). Ricordiamoci che se il segno tra le basi nel binomio divisore è positivo, allora il falso doppio prodotto nel falso quadrato dovrà essere di segno negativo. Il falso quadrato è quindi:
\[ x^4-x^2y+y^2 \]
e vale la scomposizione:
\[ (x^2)^3+y^3=(x^2+y)(x^4-x^2y+y^2) \]
Esercizio 6
Scomponiamo il polinomio:
\[ x^4-6-x^3-3x+x^2 \]
Per comodità, riscriviamo il polinomio ordinando i suoi termini per potenze decrescenti:
\[ x^4-x^3+x^2-3x-6 \]
Il polinomio non è riconducibile ad un prodotto notevole, avendo quattro termini non è di certo un trinomio caratteristico, per cui deve essere scomposto utilizzando la regola di Ruffini.
Cercando tra i divisori del termine noto:
\[ \pm 1; \: \pm 2 \: \pm 3 \: \pm 6 \]
vediamo che il polinomio ha come radice il valore \( 2 \). Infatti per \( x=2 \) il polinomio si annulla.
Sarà possibile applicare la regola due volte. Riportiamo tutti i calcoli a seguire:

Come si può vedere dallo schema, il polinomio ottenuto dopo il primo calcolo si annulla per \( x = -1 \). Possiamo a questo punto scrivere la scomposizione:
\[ x^4-6-x^3-3x+x^2=(x-2)(x+1)(x^2+3) \]
E anche questo esercizio è finito 😉
Esercizio 7 (raccoglimento totale e cubo di un binomio)
Siamo così arrivati all’ultimo di questa serie di esercizi sulla scomposizione dei polinomi. Scomporre il polinomio:
\[ x^5+9x^4+27x^3+27x^2 \]
Dato che non c’è il termine noto (tutti i termini sono in \( x \)), questa volta non è necessario applicare la Regola di Ruffini. Proviamo piuttosto ad effettuare un raccoglimento totale con \( x^2 \):
\( x^2(x^3+9x^2+27x+27) \)
Riconosciamo nel termine fra parentesi il cubo di un binomio, per cui possiamo scrivere:
\[ x^2(x+3)^3 \]
Abbiamo quindi la scomposizione:
\[ x^5+9x^4+27x^3+27x^2 = x^2(x+3)^3 \]
Esercizi sulla scomposizione dei polinomi: conclusioni
Qui si conclude la nostra rassegna di esercizi svolti e commentati sulla scomposizione dei polinomi. Questi esercizi richiedono un po’ di inventiva, ma tutto sommato si tratta semplicemente di ragionare sulle cose studiate. 😉 Buono studio!
