Perché è importante conoscere la nozione di monomi simili? L’utilità sta nel fatto che i monomi simili possono essere sommati tra loro. Forniremo già un’anticipazione in merito nella presente lezione, per poi vedere le regole generali nella prossima. 😉
Per ben comprendere la definizione di monomio simile, è importante ricordare che un monomio ridotto in forma normale è costituito da una sola parte numerica e da una parte letterale. E per riconoscere che due monomi sono simili, dobbiamo prestare la nostra attenzione esclusivamente alla parte letterale.
Definizione di monomi simili
Due o più monomi sono simili (tra loro) se hanno la stessa parte letterale. Ovvero, nella parte letterale di ciascun monomio compaiono le stesse lettere con gli stessi esponenti.
Osserviamo subito che alla definizione non interessa nulla della parte numerica dei monomi. Ciò che conta per stabilire se due monomi sono simili è esclusivamente la parte letterale.
Ad esempio, i monomi:
\[ 3x^2y, \qquad 4x^2y \]
sono simili poiché hanno la stessa parte letterale (\( x^2y \)). Infatti, le lettere presenti in ciascun monomio sono le stesse e con gli stessi esponenti.
I due monomi:
\[ 5xy; \qquad 7xyz \]
non sono simili, poiché nel monomio a destra abbiamo una lettera in più rispetto alla parte letterale del primo monomio (la lettera \( z \)).
Monomi opposti
Vediamo ora un’altra importante definizione che ci sarà davvero utile nel seguito. 😉
Due monomi si dicono opposti se hanno la stessa parte letterale e parti numeriche opposte.
Così i due monomi:
\[ 3xy, \qquad -3xy \]
sono monomi opposti poiché hanno la stessa parte letterale (\( xy \)) e hanno come parti numeriche numeri tra loro opposti.
Ricordiamo che due numeri sono tra loro opposti se hanno lo stesso valore assoluto ma segno diverso.
E’ immediato rendersi conto che i monomi opposti sono un particolare caso di monomi simili. Infatti, due monomi tra loro opposti hanno la stessa parte letterale, esattamente come ogni altra coppia o gruppo di monomi simili.
Da dove nasce l’esigenza di queste definizioni?
Nell’introduzione al calcolo letterale di Altramatica abbiamo cominciato a vedere come lavorare con quantità letterali. In particolare, si è con gradualità imparato a sviluppare espressioni piuttosto che a calcolarne il valore, passando dai numeri alle quantità letterali.
Abbiamo cominciato a vedere nello specifico la versatilità delle quantità letterali per risolvere i problemi. Vogliamo ora continuare il percorso, mostrando una pratica utilità nell’uso delle quantità letterali. Con ciò, prepareremo la strada per poter effettuare l’addizione tra monomi.
Supponiamo di avere in un cesto \( 4 \) mele, \( 3 \) pere e \( 2 \) banane. In un altro cesto, \( 2 \) mele, \( 3 \) pere e \( 5 \) banane. La domanda è: quante mele, pere e banane abbiamo in tutto?
Il problema è piuttosto elementare e vi farà senz’altro ricordare uno dei primi insegnamenti ricevuti: non possiamo sommare le mele con le pere, le banane con le susine, ecc. ecc. 😛
Tuttavia, un tale esempio è molto utile per capire l’utilità pratica della definizione di monomi simili.
In generale, è importante capire fin da subito che ogni quantità letterale rappresenta una quantità numerica che non sappiamo. Ma ciascuna lettera indica una quantità unica.
In altre parole, se abbiamo le due quantità letterali \( a \) e \( b \), in generale non abbiamo alcuna idea di quale valore abbiano. Potrebbero rappresentare gli stessi numeri, ma anche numeri diversi. E anzi, salvo diverse esplicite informazioni ipotizziamo sempre che rappresentano quantità diverse tra loro.
Siamo invece più che certi che lettere uguali rappresentano quantità uguali. Così, se abbiamo la quantità \( a \) e vogliamo raddoppiarla, scriveremo:
\[ 2a \]
e ciò evidentemente equivale a scrivere:
\[ a+a \]
Così potremo dire che:
\[ a+a=2a \]
Invece, non possiamo addizionare le quantità \( a \) e \( b \) tra loro, poiché rappresentano ciascuna una quantità numerica diversa dall’altra, che non conosciamo. Per cui, volendole addizionare potremo soltanto limitarci a lasciare la loro somma indicata:
\[ a+b \]
Così diremo che la somma tra le quantità \( a \) e \( b \) è semplicemente… \( a+b \). 🙂
Ora, torniamo ai nostri frutti e vediamo come risolvere il problema utilizzando i monomi. 😉 L’idea è quella di rappresentare ciascun insieme di frutti con un monomio. Così, scriveremo un monomio per le mele del primo cesto, un monomio per le pere del primo cesto, un monomio per le banane del primo cesto, ancora un monomio per le mele del secondo cesto e così via.
In ciascun monomio, la parte numerica indicherà la quantità di frutti uguali in un dato cesto, mentre la parte letterale indicherà quale tipo di frutto stiamo considerando. Scegliamo di indicare le mele con monomi aventi parte letterale \( m \), le pere con monomi aventi parte letterale \( p \) e le banane con la parte letterale \( b \).
Così, rappresenteremo la somma di tutti i frutti come segue:
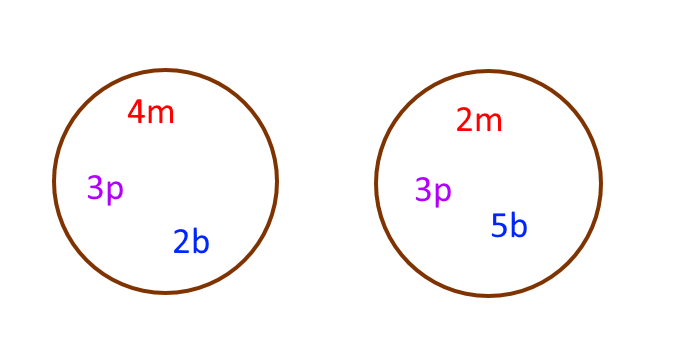
\[ 4m+2m+3p+3p+2b+5b\]
Osserviamo che nella figura, i monomi dello stesso colore sono tra loro simili.
E’ intuitivo che possiamo sommare tra loro i monomi simili poiché in questo caso rappresentano lo stesso tipo di frutto. E poiché ciascuna parte numerica rappresenta la quantità di un dato tipo di frutto in un cesto, si tratterà di sommare tra loro le parti numeriche dei monomi simili. Si ha così:
\[ (4+2)m+(3+3)p+(2+5)b = 6m+6p+7b\]
Abbiamo così risolto un problema piuttosto elementare ma in modo formale 😉 Così, non solo abbiamo capito l’utilità delle definizioni introdotte ma abbiamo praticamente spianato completamente la strada per introdurre l’addizione tra monomi, che sarà l’argomento della prossima lezione.
Ciao a tutti e buono studio, come sempre, con Altramatica! 🙂
