Come per gli altri prodotti notevoli visti, inizieremo con il calcolare il quadrato di un polinomio utilizzando la generica regola del prodotto tra polinomi, in modo da ricavare una regola specifica.
Senza ulteriori indugi, vediamo allora subito come calcolare il quadrato di un polinomio di tre o quattro termini. 🙂
Quadrato di un trinomio (quadrato di un polinomio con tre termini)
Sia da calcolare:
\[ (a+b+c)^2 \]
Per le proprietà delle potenze, possiamo riscrivere l’espressione come:
\[ (a+b+c)\cdot(a+b+c) \]
Svolgiamo il prodotto tra i due polinomi:
\[ \begin{align}&(a+b+c)\cdot(a+b+c)= \\ \\ & = a^2+ab+ac+ab+b^2+bc+ac+bc+c^2 = \\ \\ & = a^2+2ab+2ac+b^2+2bc+c^2= \\ \\ & = \boxed{a^2+b^2+c^2+2ab+2ac+2bc} \end{align} \]
Così, indicando con \( a,b,c \) tre generici monomi (ricordiamo, anche numeri), si ha la regola generale:
\[ (a+b+c)^2= a^2+b^2+c^2+2ab+2ac+2bc \]
ovvero:
il quadrato di un trinomio è uguale alla somma dei quadrati di ciascun termine del trinomio, più tre doppi prodotti, ottenuti sommando tra loro il doppio dei prodotti di ogni termine per ciascuno dei termini che lo seguono.
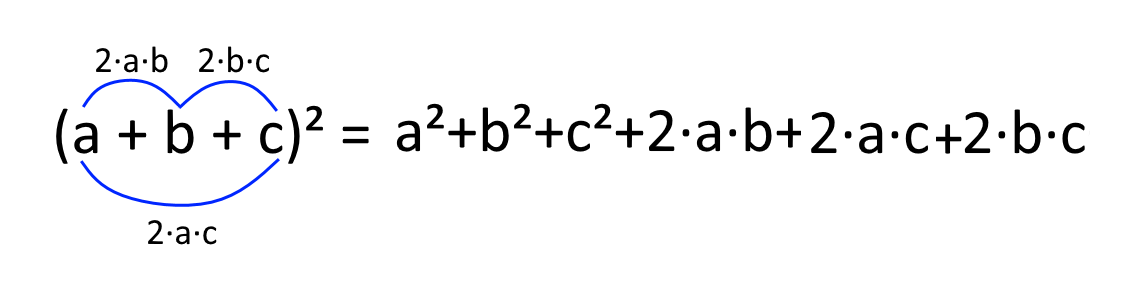
NOTA: dato che l’ultimo termine non ha ovviamente altri termini che lo seguono, a partire da esso non andrà costruito nessun doppio prodotto. 😉
ESEMPIO
\[ \begin{align}&(2x+y+k)^2=\\ \\ & = 4x^2+y^2+k^2+2\cdot2x\cdot y+2\cdot 2x \cdot k + 2 \cdot y \cdot k = \\ \\ & = 4x^2+y^2+k^2+4xy+4kx+2ky \end{align} \]
Quadrato di un quadrinomio (quattro termini)
Consideriamo il seguente quadrato:
\[ (a+b+c+d)^2 \]
Ancora una volta, riscriviamolo come prodotto tra due polinomi:
\[ (a+b+c+d)\cdot(a+b+c+d) \]
Svolgiamo i conti (ci aspettiamo una somma di \( 4 \times 4 = 16 \) termini):
\[ \small \begin{align}&(a+b+c+d)\cdot(a+b+c+d) \\ \\ & = a^2+ab+ac+ad+ab+b^2+bc+bd+ac+bc+c^2+cd+ad+bd+cd+d^2= \\ \\ & = \boxed{a^2+b^2+c^2+d^2+2ab+2ac+2ad+2bc+2bd+2cd}\end{align} \]
Questa espressione comincia ad essere piuttosto lunga ma la regola per scriverla è ancora piuttosto semplice da ricordare. 😉
Per i calcoli svolti, dati quattro generici monomi si ha, per il quadrato della loro somma (algebrica):
\[ (a+b+c+d)^2=a^2+b^2+c^2+d^2+2ab+2ac+2ad+2bc+2bd+2cd \]
ovvero:
il quadrato di un quadrinomio è uguale alla somma dei quadrati di ciascun termine del quadrinomio, più la somma di sei doppi prodotti, costruiti ciascuno moltiplicando per due il prodotto di ogni singolo termine rispettivamente per ciascuno dei termini che lo seguono.
NOTA: anche in questo caso, dato che l’ultimo termine non ha ovviamente altri termini che lo seguono, a partire da esso non andrà costruito nessun doppio prodotto. 😉
Esempio 1
\[ (a+2b+x-y)^2 \]
Dobbiamo scrivere la somma dei quadrati di ciascun termine del polinomio (quattro termini) più la somma algebrica dei doppi prodotti (sei termini). Quindi, prima di sommare eventuali termini simili, il risultato dovrà essere costituito da dieci termini. Questa considerazione ci è di aiuto per verificare la correttezza dei calcoli. 😉
Abbiamo:
\[ \begin{align}&(a+2b+x-y)^2 = \\ \\ & = a^2+(2b)^2+x^2+(-y)^2+2(a \cdot 2 b)+2ax+2a(-y)+4bx-4by-2xy= \\ \\ & = a^2+4b^2+x^2+y^2+4ab+2ax-2ay+4bx-4by-2xy \end{align} \]
Non ci sono termini simili da sommare e così questo è il risultato finale. 🙂 Effettivamente abbiamo dieci termini, per cui siamo sicuri che non manca nessun termine. Chiaramente, ciò non è sufficiente come verifica. Bisogna sempre ricontrollare di aver eseguito correttamente tutti i calcoli, e non solo che i termini siano tutti.
Esercizio 2
\[ (ab-ac+2-\dfrac{1}{2}b^2)^2 \]
Il procedimento è del tutto simile all’esercizio precedente. L’unica differenza è che dobbiamo ricordarci della proprietà delle potenze di potenze per poter calcolare il quadrato del termine \( -\dfrac{1}{2}b^2 \):
\[ \left(-\dfrac{1}{2}b^2\right)^2=\left(-\dfrac{1}{2} \right)^2b^{2 \cdot 2 }=\dfrac{b^4}{4} \]
Vediamo ora lo svolgimento.
\[ \begin{align} &(ab-ac+2-\dfrac{1}{2}b^2)^2 = \\ \\ & = a^2b^2+a^2c^2+4+\dfrac{b^4}{4}-2a^2bc+4ab-\dfrac{2}{2}ab^3-4ac+\dfrac{2}{2}ab^2c-\dfrac{4}{2}b^2= \\ \\ & = a^2b^2+a^2c^2+4+\dfrac{b^4}4{}-2a^2bc+4ab-ab^3-4ac+ab^2c-2b^2 \end{align} \]
Anche qui non abbiamo termini simili per cui questo è il risultato finale.
Per questa lezione sul quadrato di un polinomio (quadrato di un trinomio e quadrato di un quadrinomio) è tutto. Vi ricordo che potete verificare i risultati dei vostri esercizi con il risolutore per polinomi.
Nella prossima lezione vedremo il cubo di un binomio. Ciao a tutti e buono studio, come sempre, con Altramatica! 🙂
