Come sappiamo, un monomio è un particolare monomio con un solo termine. Capiamo allora che la moltiplicazione tra un polinomio e un monomio vista nella precedente lezione è semplicemente un caso particolare di moltiplicazione tra polinomi (prodotto tra polinomi).
Per cui abbiamo già una buona notizia: non siamo completamente a digiuno. Se già sappiamo come moltiplicare un polinomio per un monomio, il nostro problema sarà soltanto di estendere la regola al caso del prodotto tra due polinomi.
Per chi invece non ha presente la regola di moltiplicazione tra un polinomio e un monomio nessun problema. Nel descrivere come moltiplicare due o più polinomi tra loro partiremo da zero. 😉
Nel primo paragrafo mostreremo come ricavare la regola per moltiplicare due polinomi tra loro. Nella successiva parte della lezione, forniremo la regola generale e svolgeremo insieme alcuni prodotti tra polinomi.
Per chi ha fretta e ha bisogno direttamente della regola: click!
Moltiplicazione tra polinomi e proprietà distributiva della moltiplicazione rispetto all’addizione
Consideriamo i due polinomi:
\[ x^2+3x-7; \qquad x-2 \]
Indicheremo il loro prodotto come segue:
\[ (x^2+3x-7) \cdot (x-2) \]
Notiamo subito che è obbligatorio mettere fra parentesi entrambi i polinomi. Diversamente, le regole della precedenza delle operazioni ci porterebbero a moltiplicare soltanto l’ultimo termine del primo polinomio per il primo termine del secondo polinomio:
\[ x^2+3x-7\cdot x-2=x^2+3x-7x-2 \]
Dunque, un corretto uso delle parentesi è fondamentale per specificare quale operazione intendiamo eseguire.
Ritorniamo ora al prodotto da eseguire:
\[ (x^2+3x-7) \cdot (x-2) \]
Nell’introduzione al calcolo letterale abbiamo visto come moltiplicare tra loro due somme indicate. E qui il problema è lo stesso: dobbiamo moltiplicare tra loro due somme algebriche indicate di monomi. 😉
L’idea è quella di utilizzare una variabile che ci consenta di esprimere uno dei due polinomi come un monomio di una sola lettera. Ad esempio, scegliamo di porre:
\[ k=x-2 \]
In questo modo, tutte le volte che scriveremo \( k \), intenderemo \( x-2 \). Utilizzando la variabile \( k \), il prodotto tra polinomi precedentemente scritto diventa:
\[ (x^2+3x-7) \cdot k \]
Ora siamo in grado di calcolare agevolmente questo prodotto, poiché si tratta di un prodotto tra un polinomio e un monomio. 🙂
Ricordiamo che per calcolare tale prodotto basta applicare direttamente la proprietà distributiva della moltiplicazione rispetto all’addizione algebrica. Si ha così:
\[ (x^2+3x-7) \cdot k =x^2 \cdot k+3x \cdot k-7\cdot k \]
A questo punto cosa facciamo? Diciamo che ormai la variabile \( k \) ha svolto il suo compito. Quindi, poiché avevamo posto \( k=x-2 \), non ci resta che scrivere al posto di tutte le lettere \( k \) proprio il polinomio \( x-2 \), ovvero l’espressione che avevamo attribuito a \( k \). Si ha così:
\[ x^2 \cdot k+3x \cdot k-7\cdot k=x^2\cdot (x-2)+3x \cdot (x-2) -7\cdot (x-2) \]
Ora osserviamo che abbiamo somme di prodotti tra un polinomio e un monomio, quindi siamo in grado di sviluppare ulteriormente l’espressione:
\[ x^2\cdot (x-2)+3x \cdot (x-2) -7\cdot (x-2)=x^3-2x^2+3x^2-6x-7x+14= \]
e, sommando i termini simili:
\[= x^3+x^2-13x+14 \]
Il polinomio ottenuto è proprio il risultato della moltiplicazione tra i due polinomi dati. 😉
Il metodo qui presentato è sicuramente interessante ma non è pratico negli esercizi. Tuttavia, utilizzando la variabile \( k \) nel modo descritto abbiamo potuto capire come eseguire il prodotto. Ed è così possibile indicare una regola generale per il calcolo del prodotto tra polinomi. 😉
NOTA: assegnando alla variabile \( k \) il binomio abbiamo operato una sostituzione di variabile. Le sostituzioni di variabile saranno molto ricorrenti in Analisi.
Regola per la moltiplicazione tra due polinomi
Assegnati due polinomi, vediamo come ottenere il loro prodotto.
Si inizia moltiplicando il primo termine del primo polinomio per il primo termine del secondo polinomio, quindi sempre il primo termine del primo polinomio per il secondo termine del secondo polinomio, e così via fino ad utilizzare tutti i termini del secondo polinomio.
Nel mentre, si sommano algebricamente tra loro tutti i prodotti via via ottenuti. Ciò equivale a scrivere tutti i prodotti uno di seguito all’altro sempre completi del loro segno.
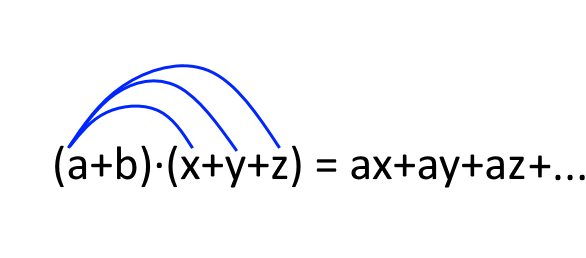
Finiti i termini del secondo polinomio, bisognerà ripetere il procedimento passando però al secondo termine del primo polinomio.
Si procederà allora moltiplicando il secondo termine del primo polinomio per il primo termine del secondo polinomio, poi sempre il secondo termine del primo polinomio per il secondo termine del secondo polinomio, e così via, sempre sommando algebricamente tra loro i prodotti via via ottenuti.
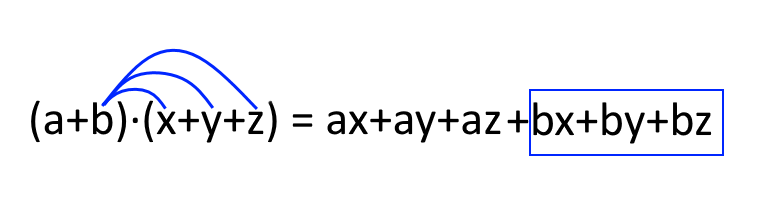
Esauriti ancora tutti i termini del secondo polinomio, si ripeterà la procedura utilizzando però il terzo termine eventualmente presente nel primo polinomio.
Si continuerà in questo modo fino ad aver esaurito tutti i termini di entrambi i polinomi.
La regola è molto simile a quella utilizzata per calcolare il prodotto cartesiano tra insiemi. 😉
ESEMPIO 1
\[ (2y^2+y)\cdot(-2y^3+y-3) \]
Possiamo rappresentare la procedura de seguire per moltiplicare i due polinomi in questo modo:
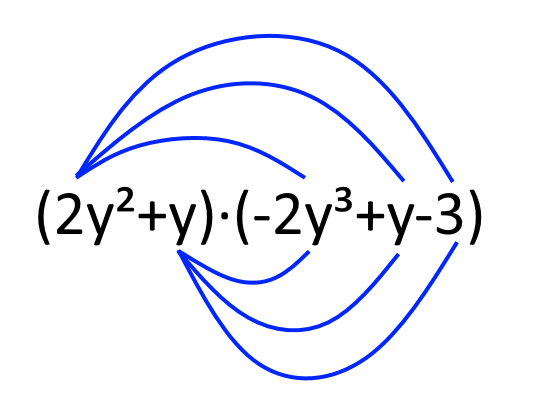
Cominciamo scrivendo i prodotti che si ottengono moltiplicando il primo termine del primo polinomio per ciascun termine del secondo polinomio:
\[ (2y^2+y)\cdot(-2y^3+y-3)=(2y^2)\cdot(-2y^3)+(2y^2)\cdot y+(2y^2)\cdot(-3)+ \dots \]
Completiamo scrivendo le somme dei prodotti tra il secondo termine del primo polinomio e tutti i termini del secondo polinomio:
\[ \begin{align}&(2y^2+y)\cdot(-2y^3+y-3)= \\ \\ & =(2y^2)\cdot(-2y^3)+(2y^2)\cdot y+(2y^2)\cdot(-3)+ \boxed{ y \cdot (-2y^3)+y \cdot y -3y}= \end{align} \]
Ora eseguiamo i prodotti tra monomi, sommando poi i termini simili:
\[ \begin{align}&=(2y^2)\cdot(-2y^3)+(2y^2)\cdot y+(2y^2)\cdot(-3)+ y \cdot (-2y^3)+y \cdot y -3y= \\ \\ & = -4y^5+2y^3\underline{-6y^2}-2y^4+\underline{y^2}-3y =-4y^5+2y^3-5y^2-2y^4-3y\end{align} \]
Abbiamo così ottenuto il prodotto cercato. 🙂
Vediamo ora ulteriori esempi.
Esempio 2 (prodotto tra un trinomio e un binomio)
\[ (4x^2-3xy+2y^2)\cdot(2x-y) \]
Vediamo di calcolare il prodotto un passo alla volta 😉 Scriviamo quindi dei risultati parziali, per mettere poi tutto insieme alla fine.
Moltiplichiamo il primo termine del primo polinomio per ciascuno dei termini del secondo polinomio, scrivendo la somma di tali prodotti:
\[ 4x^2 \cdot (2x-y)= 8x^3-4x^2y \]
Ora moltiplichiamo il secondo termine del primo polinomio sempre per tutti i termini del secondo polinomio:
\[ -3xy\cdot (2x-y)= -6x^2y+3xy^2 \]
Infine, non ci resta che moltiplicare il terzo termine del primo polinomio ancora per ciascuno dei termini del secondo polinomio:
\[ 2y^2\cdot (2x-y)=+4xy^2-2y^3 \]
Sommando tra loro tutte le somme parziali otteniamo:
\[ 8x^3-\underline{4x^2y} -\underline{6x^2y}+\underline{\underline{3xy^2}}+\underline{\underline{4xy^2}}-2y^3 \]
Sommando infine i termini simili otteniamo il risultato:
\[ 8x^3-10x^2y+7xy^2-2y^3 \]
Esempio 3 (prodotto tra un quadrinomio e un trinomio)
\[ (6a^3-8a^2-6a+81)\cdot(a^2-a+1) \]
Ora abbiamo più termini ma niente panico: il procedimento è sempre lo stesso. 😉
Dovremo semplicemente moltiplicare il primo termine del quadrinomio per ciascuno dei termini del trinomio, ottenendo una somma parziale. Poi, moltiplicheremo il secondo termine del quadrinomio ancora per ciascuno dei termini del trinomio, e così via, sommando alla fine le somme parziali via via ottenute.
Così, ad esempio, la prima somma parziale che otterremo sarà:
\[ 6a^3 \cdot (a^2-a+1)=6a^5-6a^4+6a^3 \]
Ormai non abbiamo più bisogno di scrivere le somme parziali dei prodotti separatamente. 😉 Scriviamo quindi l’intera somma dei prodotti fra i termini dei polinomi:
\[ 6a^5-6a^4+\cancel{6a^3}-8a^4+8a^3-8a^2-\cancel{6a^3}+6a^2-6a+81a^2-81a+81 \]
Infine sommando i termini simili otteniamo il risultato finale. In conclusione abbiamo:
\[ (6a^3-8a^2-6a+81)\cdot(a^2-a+1)= 6a^5-14a^4+8a^3+79a^2-87a+81 \]
Numero di termini e grado (complessivo) del prodotto ottenuto
Consideriamo il prodotto tra due polinomi ridotti in forma normale.
Il numero di termini del polinomio prodotto (cioè il risultato finale della moltiplicazione) è minore o al più uguale al prodotto fra i rispettivi numeri di termini dei polinomi fattori. Può essere minore poiché può capitare benissimo che alcuni termini siano simili. Ma, per intenderci, una volta eseguito il prodotto e prima di sommare i termini simili tra loro, avremo sicuramente un numero di termini esattamente pari al prodotto fra il rispettivo numero di termini dei polinomi di partenza.
Il grado (complessivo) del polinomio prodotto sarà invece sempre uguale alla somma dei gradi (complessivi) dei polinomi che moltiplichiamo tra loro.
Ciò è intuitivo. Infatti, il grado di un polinomio è il massimo fra i gradi dei monomi. A sua volta, il grado di un monomio ci dice da quanti fattori letterali esso è composto. Così, per le proprietà delle potenze, moltiplicando un polinomio di grado \( g_1 \) per un polinomio di grado \( g_2 \) otterremo sempre un polinomio di grado \( g_1+g_2 \). Quindi somma dei gradi e non prodotto. 😉
Consideriamo i seguenti polinomi:
\[ 2x^2+3x+5; \qquad x+3 \]
Il primo polinomio è di secondo grado, mentre il secondo polinomio è di primo grado. Inoltre, il primo polinomio è di tre termini, mentre il secondo è di due termini. Entrambi i polinomi sono ridotti a forma normale.
Così, ci aspettiamo come risultato un polinomio che sarà di terzo grado (\( 2+1 \)) e composto al massimo da \( 3 \times 2 = 6 \) termini.
Abbiamo:
\[ \begin{align} &(2x^2+3x+5) \cdot (x+3) = 2x^3+6\underline{x^2}+3\underline{x^2}+9\underline{\underline{x}}+5\underline{\underline{x}}+15= \\ \\ & = 2x^3+9x^2+14x+15\end{align} \]
Effettivamente il risultato è dato da un polinomio di terzo grado, espresso prima di sommare tra loro i termini simili dalla somma di sei termini.
In generale, una volta eseguito un prodotto tra polinomi, prima di sommare tra loro i termini simili è importante controllare il numero di termini che abbiamo. In tal modo, saremo in grado di accorgerci se per sbaglio abbiamo saltato un termine. 😉
Questa prima lezione sulla moltiplicazione tra polinomi finisce qui. Nella prossima lezione, parleremo ancora di moltiplicazione tra polinomi ma vedremo il caso di tre polinomi.
Vi ricordo infine che usando il tool per il calcolo dei polinomi online potrete verificare facilmente i risultati dei vostri esercizi sui prodotti tra polinomi.
Buon proseguimento con Altramatica!
