Cliccando sui link a seguire potrete accedere direttamente agli esercizi sul teorema di Pitagora. Diversamente, continuando a leggere potrete prima ripassare tutto ciò che serve per poter risolvere i problemi sul teorema di Pitagora. 🙂
- Esercizi facili (livello base)
- Esercizi di livello intermedio
- Problemi di livello avanzato (esercizi “difficili”)
E’ anche disponibile qui su Altramatica il comodo risolutore per problemi di Pitagora, che vi consente di verificare i risultati dei vostri esercizi. 😉
Risolvere i problemi sul teorema di Pitagora
Per lo svolgimento degli esercizi e problemi sul teorema di Pitagora è anzitutto utile una riflessione sui dati di partenza dei problemi. Nello specifico, utilizzando il teorema di Pitagora possiamo risolvere i triangoli rettangoli avendo principalmente come dati di partenza:
- le misure di due lati (relative ai due cateti oppure ad un cateto e all’ipotenusa);
- l’area del triangolo e la misura di un cateto;
- informazioni sulle somme e/o differenze tra le misure dei lati e sui rapporti tra le misure dei lati.
Ricordiamo che per misura di un lato si intende la lunghezza del segmento ad esso corrispondente. Così, quando ad esempio affermiamo che conosciamo le misure dei due cateti di un triangolo rettangolo intendiamo dire che conosciamo la lunghezza di ciascun cateto, espressa come numero. In modo del tutto simile, trovare la misura dell’ipotenusa di un triangolo rettangolo vuol dire cercare il valore che esprime la lunghezza dell’ipotenusa.
Per brevità, diremo talvolta ad esempio “trovare un cateto”, “trovare l’ipotenusa”. Tuttavia, sarà sempre sottointeso che quello che in realtà troviamo è la misura di un cateto o dell’ipotenusa.
Prima di passare ai problemi sul teorema di Pitagora, è sicuramente utile rivedere insieme alcune formule. In questo modo, potremo capire meglio gli svolgimenti degli esercizi a seguire.
Consideriamo ora la seguente figura:
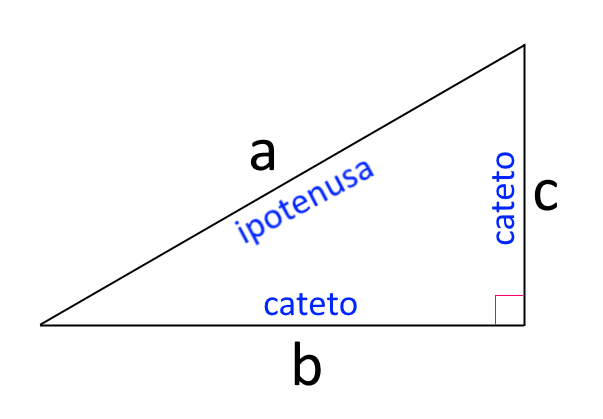
Ricordiamo che per il teorema di Pitagora valgono le formule:
\[ \begin{align} &a = \sqrt{b^2+c^2}; \\ \\ &b = \sqrt{a^2-c^2}; \\ \\ &c = \sqrt{a^2-b^2}\end{align} \]
Grazie ad esse possiamo ricavare un lato del triangolo (cateto o ipotenusa) a partire da due lati noti (entrambi i cateti o l’ipotenusa e un cateto).
Ricordiamo anche la formula dell’area di un triangolo rettangolo:
\[ A = \dfrac{b \times c }{2} \]
ovvero l’area di un triangolo rettangolo è pari al prodotto tra le misure dei suoi cateti, diviso due.
La formula è dovuta al fatto che l’area di un triangolo rettangolo è pari alla metà dell’area di un rettangolo avente per lati i cateti del triangolo rettangolo di partenza.

Come mostra intuitivamente la figura, il rettangolo di base \( b \) e altezza \( c \) ha per diagonale l’ipotenusa di ciascuno dei due triangoli rettangoli aventi cateti \( b \) e \( c \). I due triangoli rettangoli sono uguali (o congruenti) e dunque la rispettiva area è pari alla metà di quella del rettangolo.
Se dunque conosciamo un cateto e l’area di un triangolo rettangolo, possiamo ricavare l’altro cateto con una delle formule seguenti:
\[ b = \dfrac{2 \times A}{c}; \qquad c = \dfrac{2 \times A}{b} \]
Noti inoltre tutti e tre i lati del triangolo, è possibile ricavare l’altezza relativa all’ipotenusa. Consideriamo la seguente figura:

L’altezza \( h \) relativa all’ipotenusa \( a \) può essere calcolata a partire dalle misure dei cateti \( b, \: c \) e dell’ipotenusa stessa con la seguente formula:
\[ h = \dfrac{b \times c}{a} \]
L’altezza relativa all’ipotenusa di un triangolo rettangolo è dunque data dal prodotto delle misure dei cateti diviso per la misura dell’ipotenusa.
Ora, considerando l’ipotenusa e l’altezza relativa all’ipotenusa, l’area di un triangolo rettangolo può anche essere calcolata con la seguente formula:
\[ A=\dfrac{a \times h}{2} \]
E’ anche opportuno ricordare che il perimetro di un triangolo rettangolo è dato dalla somma (delle misure) dei cateti e dell’ipotenusa:
\[ P = a + b+ c \]
Infine, per le unità di misura, ricordiamo sempre che le misure dei lati e i perimetri si esprimono in unità di misura che non hanno esponenti indicati (es., \( cm, \: dm, \: m \)), mentre le aree si esprimono con unità che contengono l’esponente \( 2 \) (es., \( cm^2, \: dm^2, \: m^2 \)).
Fatte le doverose premesse, vediamo insieme alcuni esercizi e problemi sul teorema di Pitagora. 🙂
Prima parte: esercizi sul teorema di Pitagora facili (es. 1 – 2)
Esercizio 1
Calcolare il perimetro e l’area di un triangolo rettangolo avente cateti di misura 25 cm e 60 cm.

Il primo passo è ricavare l’ipotenusa:
\[ a = \sqrt{b^2+c^2}=\sqrt{60^2+25^2}=\sqrt{3600+625}=\sqrt{4225}=65 cm \]
Procediamo con il calcolo del perimetro. Lo possiamo fare perché ora conosciamo le misure di tutti e tre i lati del triangolo:
\[ P = a+b+c=65+60+25=150 cm \]
Concludiamo l’esercizio calcolando l’area del triangolo:
\[ A = \dfrac{b \times c}{2}=\dfrac{60 \times 25}{2}=30 \times 25 = 750cm^2 \]
Esercizio 2
Calcolare perimetro e area di un triangolo rettangolo avente ipotenusa \( 45 cm \) e uno dei due cateti \( 36 cm \).
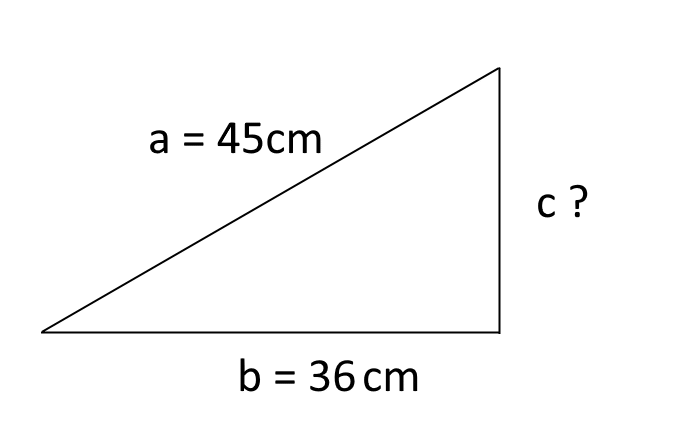
Calcoliamo il cateto mancante:
\[ c = \sqrt{a^2-b^2}=\sqrt{45^2-36^2}=\sqrt{2025-1296}=\sqrt{729}=27cm \]
Veniamo ora al perimetro:
\[ P = a+b+c = 45+36+27= 108cm \]
Infine, per l’area:
\[ A = \dfrac{b \times c}{2}=\dfrac{36 \times 27}{2}=486 cm^2 \]
Esercizi sul teorema di Pitagora di livello intermedio (es. 3 – 4)
Esercizio 3
La somma delle misure dell’ipotenusa e di un cateto di un triangolo rettangolo è pari a \( 54 \) cm, e quello stesso cateto è \( \dfrac{5}{13} \) dell’ipotenusa. Calcolare perimetro e area del triangolo.
In questo tipo di problemi, dobbiamo anzitutto capire a quale grandezza attribuire la lettera \( x \) (ove con \( x \) intendiamo una quantità che dobbiamo trovare).
In particolare, nel problema considerato viene detto che la misura di un cateto è pari a \( \dfrac{5}{13} \) dell’ipotenusa.
Osserviamo anzitutto che il problema è ben posto poiché la frazione \( \dfrac{5}{13} \) è propria, e di conseguenza il cateto risulterà correttamente di misura inferiore rispetto a quella dell’ipotenusa. Ricordiamo che una frazione propria rappresenta una quantità sempre minore di \( 1 \), e quindi moltiplicando una frazione propria per una certa grandezza, otteniamo come risultato una grandezza più piccola. Per approfondire quest’ultimo aspetto: classi di equivalenza e frazioni viste come operatori.
Tornando al problema, dobbiamo indicare con \( x \) la misura dell’ipotenusa e con \( \dfrac{5}{13}x \) la misura di uno dei cateti.
Poiché nel testo ci viene detto che la somma dell’ipotenusa e del cateto considerato è pari a \( 54cm \), possiamo scrivere:
\[ x + \dfrac{5}{13}x=54cm \]
Osserviamo che \( \dfrac{13}{13} \) è una frazione apparente che equivale al valore \( 1 \). E’ quindi possibile riscrivere la precedente come:
\[ \dfrac{13}{13}x+\dfrac{5}{13}x=54cm \qquad (*) \]
Leggiamo attentamente: abbiamo i \( 13/13 \) di una quantità sommati ai \( 5/13 \) di quella stessa quantità. Se ad esempio consideriamo la metà dell’unità sommata alla metà ancora dell’unità, è intuitivo che avremo come risultato della somma l’intera unità, ovvero \( \dfrac{1}{2}+\dfrac{1}{2}=1 \). Nel nostro caso dovremo quindi sommare le frazioni della quantità \( x \) presenti, e applicare la frazione risultato della somma di nuovo alla quantità \( x \). Si ha così:
\[ \dfrac{13}{13}x+\dfrac{5}{13}x=\left(\dfrac{13}{13}+\dfrac{5}{13} \right)x=\dfrac{13+5}{13}x=\dfrac{18}{13}x \]
Così, la precedente uguaglianza (*) si può ora riscrivere come:
\[ \dfrac{18}{13}x=54cm \]
Ora, poiché la \( x \) moltiplicata per una quantità è uguale a \( 54cm \), possiamo agevolmente intuire che la \( x \) sarà pari a \( 54cm \) diviso la quantità che la moltiplica. Scriviamo quindi:
\[ x = 54 : \dfrac{18}{13}=54 \cdot \dfrac{13}{18}=\cancel{54}^{\small \displaystyle3} \cdot \dfrac{13}{\cancel{18}}=39cm \]
Ricordiamo: \( x \) rappresenta l’ipotenusa, che indicheremo come negli altri esercizi con la lettera \( a \). Così, abbiamo trovato che il triangolo ha ipotenusa pari ad \( a = 39cm \). Poiché la somma di un cateto e dell’ipotenusa è pari a \( 54cm \), è ora immediato ricavare la misura del cateto (indichiamolo ad esempio con \( b \)):
\[ b = 54 – 39 = 15 cm \]
Noti l’ipotenusa e un cateto, possiamo ricavare il rimanente cateto:
\[ c = \sqrt{a^2-b^2}=\sqrt{39^2-15^2}=\sqrt{1521-225}=\sqrt{1296}=36 cm \]
Veniamo ora al calcolo del perimetro del triangolo dato:
\[ P=a+b+c=39+15+36=90cm \]
Infine, calcoliamone l’area:
\[ A = \dfrac{b \times c}{2}=\dfrac{15 \times 36}{2}=270cm^2 \]
Il problema è così risolto. 😉
Esercizio 4
Un cateto di un triangolo rettangolo è \( 48 cm \) e l’altro cateto è \( \dfrac{3}{4} \) del primo cateto. Calcolare la misura dell’altezza relativa all’ipotenusa.
Per poter calcolare l’altezza relativa all’ipotenusa dobbiamo conoscere le misure di tutti e tre i lati del triangolo. Ci è nota la misura di un cateto, che indichiamo ad esempio con \( b = 48cm \). Praticamente già abbiamo le misure dei due cateti, poiché la misura mancante si ricava immediatamente da quella data:
\[ c = \dfrac{3}{4}b=\dfrac{3}{\cancel{4}}\times \cancel{48}^{\small \displaystyle12} = 36cm \]
Ora grazie al teorema di Pitagora possiamo ricavare la misura dell’ipotenusa:
\[ a = \sqrt{b^2+c^2}=\sqrt{48^2+36^2}=\sqrt{2304+1296}=\sqrt{3600}=60cm \]
Utilizzando la formula opportuna, ricaviamo la misura dell’altezza relativa all’ipotenusa. Ricordiamo, questa si ottiene dividendo il prodotto delle misure dei cateti per la misura dell’ipotenusa:
\[ h=\dfrac{b \times c}{a}=\dfrac{48 \times 36}{60}=\dfrac{1728}{60}=28,8cm \]
Esercizi sul teorema di Pitagora di livello medio-avanzato (es. 5 – 6)
Esercizio 5
Un triangolo ha misura dell’ipotenusa pari a \( 50cm \) e altezza relativa all’ipotenusa uguale a \( 24cm \). Determinare le misure dei due cateti.
Per risolvere il problema è importante osservare che in un triangolo rettangolo la mediana relativa all’ipotenusa è pari alla metà della misura dell’ipotenusa.
Per comprendere tale proprietà, rappresentiamo un triangolo rettangolo inscritto in una circonferenza:

La mediana relativa all’ipotenusa coincide con un raggio della circonferenza entro la quale è inscritto il triangolo. Osserviamo inoltre che l’ipotenusa coincide con un diametro della circonferenza. Poiché la misura di un raggio è la metà della misura di un diametro, la mediana \( m \) avrà di conseguenza lunghezza pari alla metà dell’ipotenusa.
Così abbiamo:
\[ m = \dfrac{a}{2}=\dfrac{50}{2}=25cm \]
Poiché \( \overline{AH} \) ci è nota in quanto misura dell’altezza relativa all’ipotenusa, grazie al teorema di Pitagora possiamo ricavare \( \overline{OH} \):
\[ \overline{OH}=\sqrt{m^2-\overline{AH}^2}=\sqrt{25^2-24^2}=7cm \]
Per ricavare i cateti \( \overline{AB} \) e \( \overline{AC} \) ragioniamo sui triangoli rettangoli \( ABH \) e \( ACH \).
Intanto è utile osservare che:
\[ \overline{BO}=\overline{CO}=\dfrac{a}{2} \]
Si ha così:
\[ \overline{BH}=\overline{BO}+\overline{OH}=\dfrac{a}{2}+\overline{OH}=\dfrac{50}{2}+7=32cm \]
Applicando il teorema di Pitagora al triangolo \( ABH \) otteniamo:
\[ \overline{AB}=\sqrt{\overline{BH}^2+\overline{AH}^2}=\sqrt{32^2+24^2}=40cm \]
Per il triangolo \( AHC \), ricaviamo la misura del cateto \( \overline{CH} \) come:
\[ \overline{CH}=\overline{CO}-\overline{OH}=\dfrac{a}{2}-\overline{OH}=\dfrac{50}{2}-7=18cm \]
Infine, applicando ancora il teorema di Pitagora allo stesso triangolo \( \overline{AHC} \):
\[ \overline{AC}=\sqrt{\overline{CH}^2+\overline{AH}^2}=\sqrt{18^2+24^2}=30cm \]
ed anche questo problema sul teorema di Pitagora è così risolto. 🙂
Passiamo ora all’ultimo di questi esercizi (problemi) sul teorema di Pitagora.
Esercizio 6
E’ dato un triangolo avente area \( 864cm^2 \) e un cateto \( b = 48cm \). Calcolare perimetro, altezza relativa all’ipotenusa e misure delle proiezioni dei cateti sull’ipotenusa.
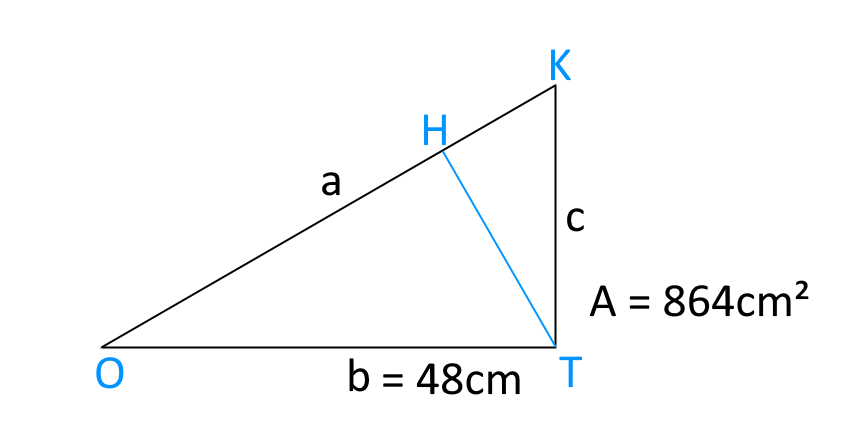
Le proiezioni dei cateti sull’ipotenusa sono date dai segmenti \( \overline{OH} \) e \( \overline{HK} \). Il segmento \( \overline{HT} \) è l’altezza relativa all’ipotenusa.
Poiché l’area di un triangolo è data da:
\[ A = \dfrac{b \times c}{2} \]
nel nostro caso avremo:
\[ 864 = \dfrac{48 \times c}{2} \]
e possiamo ricavare il cateto \( c \):
\[ c = \dfrac{864 \times 2}{48}=36 cm \]
Noti i cateti, grazie al teorema di Pitagora possiamo ricavare l’ipotenusa:
\[ a = \sqrt{b^2+c^2}=\sqrt{48^2+36^2}=60cm \]
Così, il perimetro è dato da:
\[ p=a+b+c=60+48+36=144cm \]
Ora calcoliamo l’altezza relativa all’ipotenusa:
\[ \overline{HT}=\dfrac{b \times c}{a}=\dfrac{48 \times 36}{60}=28,8cm \]
Veniamo ora alle proiezioni dei cateti sull’ipotenusa. Riepiloghiamo in figura i dati dei quali disponiamo e cosa dobbiamo ricavare:

Si tratta di ragionare separatamente sui triangoli rettangoli \( OHT \) e \( THK \). In particolare, dobbiamo applicare il teorema di Pitagora a ciascuno di essi. Ognuna delle proiezioni che dobbiamo ricavare è infatti un cateto rispettivamente di ciascuno di questi triangoli.
Consideriamo il triangolo rettangolo \( OHT \). Esso ha come ipotenusa il cateto \( b \) del triangolo di partenza (corrispondente al segmento \( \overline{OT} \)) ed ha un cateto uguale all’altezza relativa all’ipotenusa sempre del triangolo di partenza (ovvero, il segmento \( \overline{HT} \)). Applicando così il teorema di Pitagora al triangolo \( OHT \) abbiamo:
\[ \overline{OH}=\sqrt{b^2-\overline{HT}^2}=\sqrt{48^2-28,8^2}=38,4cm \]
Lavorando in modo del tutto simile nel triangolo \( THK \) otteniamo:
\[ \overline{HK}=\sqrt{c^2-\overline{HT}^2}=\sqrt{36^2-28,8^2}=21,6cm \]
Abbiamo così risolto anche questo problema su Pitagora. 😉
Questa scheda sugli esercizi sul teorema di Pitagora termina qui. Vi ricordo ancora il pratico tool risolvere i problemi con il teorema di Pitagora online. Ciao a tutti! 🙂
