I lati noti del triangolo rettangolo potranno essere i due cateti, oppure un cateto e l’ipotenusa. In entrambi i casi sarà possibile ricavare il lato mancante (cateto o ipotenusa).
Il teorema di Pitagora non fornisce direttamente delle formule per ricavare il lato che non conosciamo, tuttavia queste possono essere ricavate agevolmente a partire dall’enunciato del teorema di Pitagora stesso.
Se già conoscete il teorema di Pitagora e siete alla ricerca di esercizi svolti: problemi ed esercizi sul teorema di Pitagora, svolti e commentati.
E’ inoltre disponibile su Altramatica il pratico tool: risolvere i problemi sul teorema di Pitagora online. Questo comodo strumento permette di verificare immediatamente i risultati dei vostri esercizi. 😉
Senza ulteriori indugi, vediamo subito l’enunciato del teorema di Pitagora, una sua semplice dimostrazione e qualche esempio sul suo utilizzo.
Enunciato del teorema di Pitagora
In un triangolo rettangolo, l’area del quadrato costruito sull’ipotenusa è uguale alla somma delle aree dei quadrati costruiti sui cateti.
Ciò significa che se consideriamo, a partire da un certo triangolo rettangolo:
- un quadrato di area \( A_1 \) il cui lato ha la stessa lunghezza dell’ipotenusa del triangolo rettangolo;
- un quadrato di area \( A_2 \) il cui lato ha la stessa lunghezza di un cateto del triangolo rettangolo;
- infine, un quadrato di area \( A_3 \) il cui lato ha la stessa lunghezza dell’altro cateto del triangolo rettangolo,
allora si ha:
\[ A_1 = A_2 + A_3 \]
Osserviamo la seguente figura:
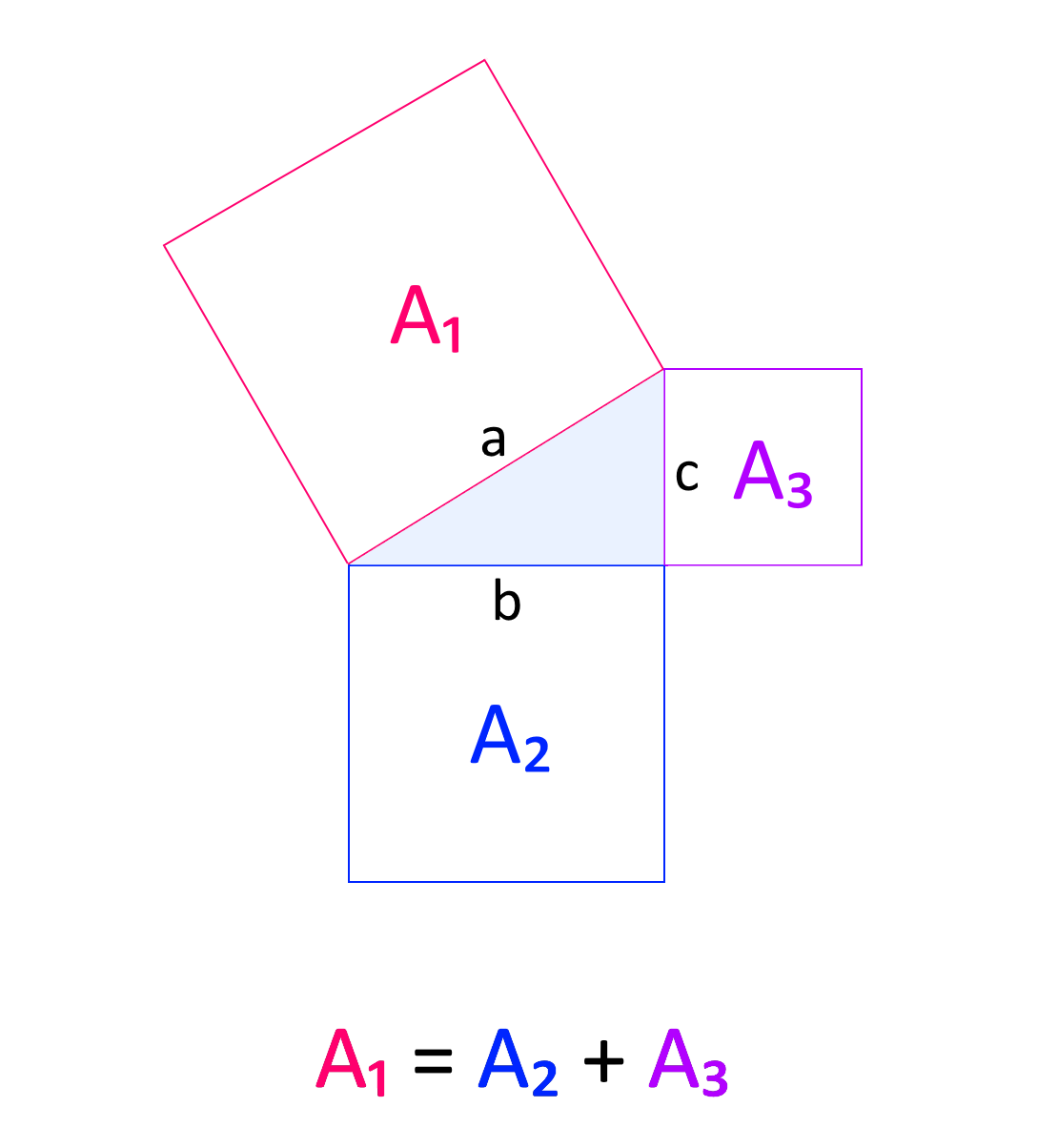
Detta \( a \) la misura dell’ipotenusa e indicate con \( b \) e \( c \) le rispettive misure dei cateti del triangolo rettangolo, avremo che:
\[ A_1 = a \times a = a^2; \qquad A_2 = b \times b = b^2; \qquad A_3 = c \times c = c^2 \]
e l’enunciato del teorema di Pitagora si può esprimere come:
\[ \boxed{a^2 = b^2 + c^2} \]
Si hanno anche le seguenti formule inverse:
\[ \begin{align}&b^2 = a^2-c^2 \\ \\ &c^2=a^2-b^2 \end{align} \]
Formule per ricavare un cateto o l’ipotenusa di un triangolo rettangolo con il teorema di Pitagora
Le precedenti formule ci consentono di ricavare le aree (o superfici) dei quadrati costruiti su ciascun lato del triangolo rettangolo dato. Tuttavia, utilizzando la radice quadrata, dalle precedenti formule otteniamo delle nuove formule che ci permettono di ricavare direttamente la misura del lato incognito (per misura intendiamo semplicemente la lunghezza).
La seguente formula permette di ricavare la misura dell’ipotenusa a partire dalle misure dei cateti:
\[ a = \sqrt{b^2+c^2} \]
Mentre le seguenti formule consentono di ricavare il cateto del quale non conosciamo la misura a partire dalle misure dell’ipotenusa e dell’altro cateto:
\[ \begin{align}& b=\sqrt{a^2-c^2} \\ \\ & c=\sqrt{a^2-b^2}\end{align} \]
Queste sono le formule di utilizzo pratico per risolvere i triangoli rettangoli con il teorema di Pitagora.
Due precisazioni che aiutano ad utilizzare le formule correttamente:
- in un triangolo rettangolo, l’ipotenusa è sempre il lato maggiore. Così, i cateti avranno sempre misura minore rispetto a quella dell’ipotenusa;
- quanto è dentro al simbolo di radice deve avere sempre come risultato un numero positivo. Così, attenzione a scrivere correttamente la formula da usare quando dobbiamo ricavare un cateto. Nella differenza dentro la radice, la quantità da scrivere prima (minuendo) è sempre il quadrato dell’ipotenusa. 😉
Passiamo ora alla dimostrazione, scelta fra le tantissime alternative possibili in modo da essere ragionevolmente comprensibile e semplice da ricordare.
Per chi ancora non ha visto il calcolo letterale, la spiegazione sotto spoiler disponibile a seguire dovrebbe essere di aiuto. Precisiamo per questi lettori che l’operazione di moltiplicazione si può indicare anche con il punto centrale. In ogni caso, tutto sarà chiaro in terza media, ma comunque invito anche gli studenti della seconda media a dare un’occhiata alla dimostrazione.
Una dimostrazione del teorema di Pitagora
Consideriamo il seguente disegno:
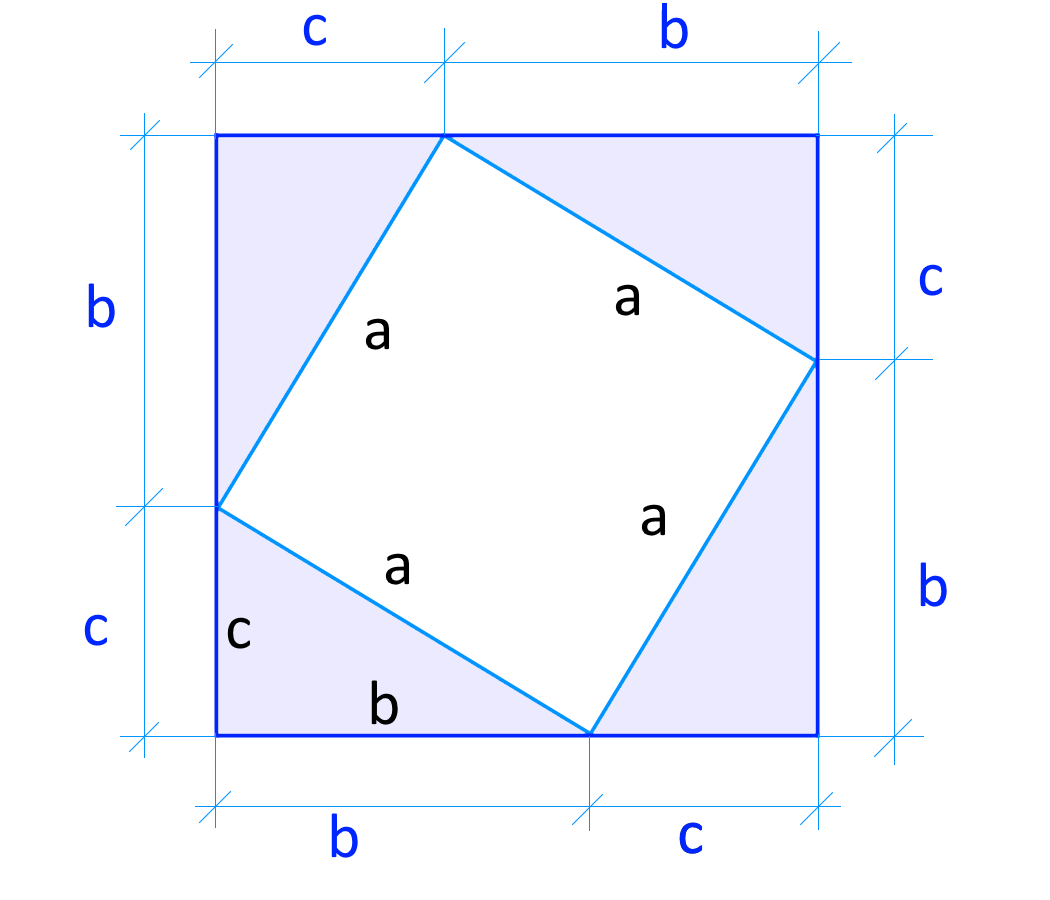
Si tratta di un quadrato inclinato avente lato \( a \) che è inscritto in un quadrato di lato \( b+c \). All’interno abbiamo quattro triangoli rettangoli uguali, tutti aventi ipotenusa pari ad \( a \) e cateti pari a \( b \) e \( c \).
E’ immediato osservare che la somma tra l’area del quadrato inscritto e quattro volte l’area del triangolo rettangolo avente lati \( a \), \( b \) e \( c \) è pari all’area del quadrato grande avente lato \( b+c \).
L’area del quadrato grande è data da:
\[ A_{\text{quadrato_grande}}=(b+c)^2=b^2+2bc+c^2 \]
Per chi deve ancora studiare il quadrato di un binomio, per calcolare il quadrato della somma indicata \( b+c \) possiamo cavarcela con la proprietà distributiva della moltiplicazione. Consideriamo una certa quantità \( k \). In base a questa proprietà è chiaro che:
\[ (b+c)\cdot k = b \cdot k + c \cdot k \]
Ora, sostituiamo al posto della lettera \( k \) la quantità \( b+c \), ed applichiamo di nuovo la proprietà distributiva della moltiplicazione al risultato appena ottenuto:
\[ \begin{align}&b \cdot k + c \cdot k = b \cdot (b+c) + c \cdot (b + c) = \\ \\ & =b \cdot b + b \cdot c + c \cdot b + c \cdot c =b^2 + b\cdot c + b \cdot c + c ^2 =b^2 + 2\cdot b \cdot c+c^2 \end{align} \]
Ed ecco fatto. 🙂
Nei passaggi abbiamo calcolato \( b \cdot c + b \cdot c = 2 \cdot b \cdot c \). Ciò è intuitivo poiché il prodotto di due quantità ancora sommato per il prodotto di quelle stesse quantità sarà ovviamente pari a due volte quello stesso prodotto. 😉
Ancor più intuitivo è dire \( b \cdot b = b^2 \), in quanto per le potenze il prodotto di due fattori tra loro uguali è pari al quadrato di uno dei due fattori. Ad esempio, \( 2 \cdot 2 = 2^2 \), e così \( b \cdot b = b^2 \) e \( c \cdot c = c^2 \).
In conclusione quanto ricavato è proprio ciò che volevamo, poiché avendo posto \( b+c=k \), allora \( (b+c)\cdot k= (b+c)\cdot(b+c)=(b+c)^2 \).
Ora, poiché l’area di un triangolo rettangolo è pari al prodotto dei cateti diviso due, la somma delle aree di tutti i triangoli rettangoli nel disegno sarà data da:
\[ A_{\text{triangoli}}=4 \cdot \left( \dfrac{b\cdot c}{2}\right)=2 \cdot b \cdot c \]
Mentre l’area del quadrato inscritto è:
\[ A_{\text{quadrato_inscritto}}=a^2 \]
Così, avremo che:
\[ A_{\text{quadrato_grande}}=A_{\text{triangoli}}+A_{\text{quadrato_inscritto}} \]
ovvero, sostituendo a ciascuna area la sua espressione in funzione dei lati:
\[ b^2+2 \cdot b \cdot c+c^2=2\cdot b\cdot c +a^2 \]
e sottraendo a ciascuna espressione a sinistra e a destra dell’uguale la quantità \( 2 \cdot b \cdot c \) otteniamo in conclusione:
\[ b^2+c^2=a^2 \]
il che dimostra il teorema di Pitagora. 😉
Esempi
Esempio 1
Calcolare la misura dell’ipotenusa del seguente triangolo rettangolo, noti i cateti:

Poiché conosciamo le misure dei cateti, dovremo usare la formula:
\[ a = \sqrt{b^2+c^2} \]
e quindi, nel nostro caso:
\[ a= \sqrt{30^2+15^2}=\sqrt{900+225}=\sqrt{1125}\approx 33,54 \]
Per gli studenti delle superiori, proviamo se magari è possibile esprimere il risultato in maniera esatta. Abbiamo:
\[ 1125 = 3^2 \cdot 5^3 \]
Così:
\[ \sqrt{1125}=\sqrt{3^2 \cdot 5^3}=3 \sqrt{5 \cdot 5^2}=3 \cdot 5 \cdot \sqrt{5}=15 \sqrt{5} \]
In conclusione, la misura dell’ipotenusa espressa in forma esatta è pari a \( 15 \cdot \sqrt{5} \).
Esempio 2
Calcolare la misura del cateto \( b \) del seguente triangolo rettangolo, note le misure dell’ipotenusa e dell’altro cateto:

Dovremo stavolta usare la formula:
\[ b = \sqrt{a^2-c^2} \]
e quindi:
\[ b = \sqrt{16^2-8^2}=\sqrt{256-64}=\sqrt{192}\approx 13,85 \]
Ancora per gli studenti delle superiori, proviamo ad esprimere il risultato ottenuto in forma esatta:
\[ \sqrt{192}=\sqrt{2^6 \cdot 3 }=2^3 \sqrt{3}=8 \sqrt{3} \]
Così, \( b=8 \sqrt{3} \).
Per quanto riguarda il teorema di Pitagora, concludiamo qui. Vi ricordo la relativa esercitazione: problemi sul teorema di Pitagora, svolti e commentati.
Nella prossima lezione vedremo una introduzione allo studio dei triangoli rettangoli con le funzioni trigonometriche. Ciao a tutti e buono studio con Altramatica! 🙂
