NOTA: per gli studenti della scuola media, la scheda di esercizi da utilizzare è quella relativa ai problemi sul teorema di Pitagora.
Negli esercizi e problemi sui triangoli rettangoli potremo avere in alternativa i seguenti dati di partenza:
- i due cateti;
- l’ipotenusa e un cateto;
- l’ipotenusa e un angolo acuto;
- un cateto e un angolo acuto.
Osserviamo che in tutti questi casi il triangolo rettangolo è univocamente determinato e di conseguenza sarà possibile risolverlo.
Nei primi due casi è sufficiente il teorema di Pitagora poiché sono noti due lati del triangolo rettangolo. Nel terzo e quarto caso dobbiamo invece per forza ricorrere ai teoremi dei triangoli rettangoli.
Per gli esercizi e problemi sui triangoli rettangoli di questa scheda utilizzeremo la seguente figura di riferimento:

Per i teoremi dei triangoli rettangoli valgono le seguenti relazioni:
\[ \begin{align}&b = \cos \gamma \cdot a ; \quad &b = \sin \beta \cdot a\\ \\ &c = \cos \beta \cdot a; \quad &c = \sin \gamma \cdot a \\ \\ &b = \tan \beta \cdot c ; \quad &b = \cot \gamma \cdot c\end{align} \]
e le loro inverse, che ricordiamo si possono ottenere grazie al secondo principio di equivalenza. Ad esempio, data la formula:
\[ b = \cos \gamma \cdot a; \qquad (*) \]
per ricavare \( a \) scriveremo:
\[ \dfrac{b}{\cos \gamma} = \dfrac{ \cos \gamma \cdot a}{\cos \gamma} \]
e quindi:
\[ a = \dfrac{b}{\cos \gamma} \qquad (**) \]
Osserviamo che dalla (*) otteniamo la (**) semplicemente spostando al denominatore del primo membro la quantità che moltiplica l’incognita al secondo membro. Quindi, la (**) può ricavarsi dalla (*) in modo immediato, evitando il passaggio intermedio.
La (*) può infatti essere riguardata come un’equazione di primo grado in forma normale, nella quale \( a \) è l’incognita, \( \cos \gamma \) il coefficiente del termine che contiene l’incognita e \( b \) il termine noto. L’approccio seguito equivale così all’uso della formula risolutiva delle equazioni di primo grado.
Allo stesso modo, dalla formula:
\[ b = \tan \beta \cdot c \]
otteniamo la formula inversa:
\[ c = \dfrac{b}{\tan \beta} \]
Fatte le dovute premesse, vediamo subito gli esercizi sui triangoli rettangoli. 🙂
Esercizio 1
Risolvere il triangolo rettangolo in figura dati \( a = 10 \) e \( \beta = 30° \).
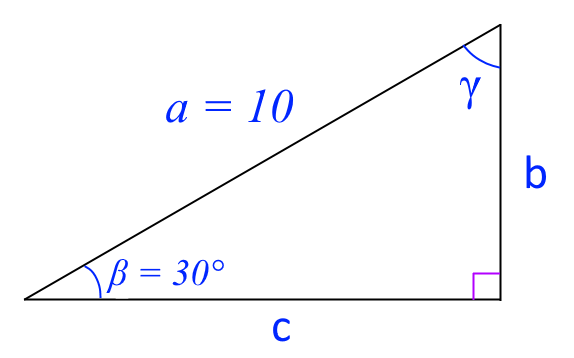
Come dati di partenza abbiamo la misura dell’ipotenusa e l’ampiezza dell’angolo adiacente al cateto \( c \). Il primo teorema sui triangoli rettangoli ci dice che il cateto adiacente ad un angolo si può ottenere a partire dall’ipotenusa moltiplicando il coseno dell’angolo stesso per la misura dell’ipotenusa.
Per il primo teorema dei triangoli rettangoli possiamo allora calcolare la misura del cateto \( c \):
\[ \begin{align}c &= \cos \beta \cdot a= \\ \\ &= \cos (30°) \cdot 10 = \dfrac{\sqrt{3}}{2}\cdot10=\dfrac{\sqrt{3}}{2}\cdot5\cdot2=5 \sqrt{3} \end{align} \]
Proviamo ora a ricavare la misura del cateto \( b \). Il secondo teorema sui triangoli rettangoli afferma che possiamo calcolare la misura di un cateto conoscendo uno dei due angoli acuti e la misura dell’altro cateto. Nel nostro caso abbiamo la misura del cateto \( b \) e dell’angolo ad esso opposto. Dobbiamo quindi utilizzare la funzione tangente, applicando il secondo teorema dei triangoli rettangoli come segue:
\[ b = \tan \beta \cdot c= \tan (30°)\cdot5 \sqrt{3} = \dfrac{\sqrt{3}}{3}\cdot5 \sqrt{3}=\dfrac{15}{3}=5 \]
Ora, poiché la somma degli angoli di un qualunque triangolo è pari a \( 180° \), e poiché in un triangolo rettangolo un angolo è necessariamente pari a \( 90° \) (angolo retto), si ha:
\[ \gamma = 90° – \beta = 90°-30°=60° \]
Il triangolo è così risolto.
Esercizio 2
Risolvere un triangolo come quello nell’esercizio precedente ma nel caso in cui sia \( a = 6 \) e \( \beta = \dfrac{\pi}{3} \).
Proviamo ad utilizzare questa volta anche l’angolo \( \gamma \):
\[ \gamma = \dfrac{\pi}{2}- \beta = \dfrac{\pi}{2}- \dfrac{\pi}{3} = \dfrac{\pi}{6} \]
Per il primo teorema dei triangoli rettangoli:
\[ c = \sin \gamma \cdot a = \sin \dfrac{\pi}{6}\cdot6 =\dfrac{1}{2}\cdot6=3 \]
Infine, utilizzando sempre il primo teorema dei triangoli rettangoli e l’angolo \( \beta \):
\[ b = \sin \beta \cdot a = \sin \dfrac{\pi}{3}\cdot 6 = \dfrac{\sqrt{3}}{2}\cdot6 = 3 \sqrt{3} \]
Esercizio 3
Risolvere il seguente triangolo rettangolo, noti \( b = 18 \) e \( \beta = 60° \).

Iniziamo ricavando l’angolo \( \gamma \):
\[ \gamma = 90°-\beta = 90-60=30° \]
Ora, utilizziamo il secondo teorema dei triangoli rettangoli in modo da ricavare il cateto \( c \):
\[ c= \tan \gamma \cdot b= \tan (30°) \cdot 18 = \dfrac{\sqrt{3}}{3}\cdot18 =6\sqrt{3} \]
In alternativa avremmo potuto anche usare la cotangente, ma con l’angolo \( \beta \):
\[ c = \cot \beta \cdot b = \cot (60°) \cdot b = \dfrac{\sqrt{3}}{3}\cdot 18=6 \sqrt{3} \]
Ci rimane da calcolare la misura dell’ipotenusa. Poiché abbiamo le misure dei due cateti, potremmo usare il teorema di Pitagora. In alternativa, possiamo anche usare il primo teorema dei triangoli rettangoli. Con quest’ultima scelta si ha:
\[ c = \cos \beta \cdot a\quad \Rightarrow \quad a = \dfrac{c}{\cos \beta }=\dfrac{6 \sqrt{3}}{\cos(60°)}= 12 \cdot \sqrt{3} \]
Abbiamo così risolto anche questo triangolo. 🙂
I seguenti esercizi sono un po’ meno agevoli. Concettualmente, non richiedono niente di nuovo. Tuttavia, gli angoli in gioco non sono notevoli e la valutazione delle funzioni trigonometriche per tali angoli richiede qualche trucchetto (in particolare, utilizzeremo ad esempio le formule di bisezione e le formule di addizione).
Esercizio 4
Risolvere un triangolo come i precedenti dati però i valori \( a=4 \) e \( \beta = \dfrac{\pi}{12} \).
La complicazione in questo esercizio è data dal valutare la funzione seno per l’angolo \( \dfrac{\pi}{12} \). In questi casi è possibile cavarsela con delle tabelle (anche se devono essere molto complete). Tuttavia, vedremo di arrangiarci solo a partire dai valori delle funzioni trigonometriche per gli angoli notevoli. 😉
Osserviamo che \( \dfrac{\pi}{12} \) è la metà dell’angolo noto \( \dfrac{\pi}{6} \). Di conseguenza, per la formula di bisezione del seno:
\[ \sin \left(\dfrac{\pi}{12} \right)=\sqrt{\dfrac{1-\cos\left( \dfrac{\pi}{6}\right)}{2}}=\sqrt{\dfrac{1-\dfrac{\sqrt{3}}{2}}{2}}=\sqrt{\dfrac{2-\sqrt{3}}{4}} \]
Ora dobbiamo utilizzare la formula dei radicali doppi:
\[ \begin{align} &\sqrt{\dfrac{2-\sqrt{3}}{4}}=\dfrac{1}{2}\left( \sqrt{\dfrac{2+\sqrt{4-3}}{2}} – \sqrt{\dfrac{2-\sqrt{4-3}}{2}}\right)= \\ \\ & = \dfrac{1}{2} \left( \sqrt{\dfrac{2+1}{2}} – \sqrt{\dfrac{2-1}{2}}\right)= \\ \\ & = \dfrac{1}{2} \left(\sqrt{\dfrac{3}{2}} – \sqrt{\dfrac{1}{2}}\right) = \dfrac{1}{2}\left(\dfrac{\sqrt{3}}{\sqrt{2}}-\dfrac{1}{\sqrt{2}} \right) = \\ \\ & = \dfrac{1}{2}\left(\dfrac{\sqrt{3}-1}{2} \cdot \dfrac{\sqrt{2}}{\sqrt{2}}\right) = \dfrac{1}{2} \left(\dfrac{\sqrt{3}\sqrt{2}-\sqrt{2}}{2} \right) = \\ \\ & = \dfrac{\sqrt{3}\sqrt{2}-\sqrt{2}}{4} = \dfrac{\sqrt{2}(\sqrt{3}-1)}{4}\end{align} \]
Possiamo così scrivere, applicando il primo teorema dei triangoli rettangoli:
\[ \begin{align}& b = \sin \beta \cdot a = \sin \dfrac{\pi}{12}\cdot4=\dfrac{(\sqrt{3}-1)\sqrt{2}}{4}\cdot 4 =(\sqrt{3}-1)\sqrt{2}= \\ \\ & = \sqrt{3}\sqrt{2}-\sqrt{2}=\sqrt{6}-\sqrt{2} \end{align} \]
Adesso, ricaviamo l’angolo \( \gamma \):
\[ \gamma = \dfrac{\pi}{2}-\beta = \dfrac{\pi}{2}-\dfrac{\pi}{12}=\dfrac{5}{12}\pi \]
Utilizzando ora il secondo teorema dei triangoli rettangoli scriviamo:
\[ c = \tan \gamma \cdot b =\tan \left(\dfrac{5}{12} \pi\right)\cdot (\sqrt{6}-\sqrt{2}) \]
Ora abbiamo un nuovo problema: valutare \( \tan \left(\dfrac{5}{12} \pi\right) \).
Basta osservare che, per la periodicità della funzione tangente (il periodo è in particolare \( \pi \)):
\[ \tan\left(\dfrac{5}{12}\pi\right)=\tan\left(\dfrac{5}{12}\pi-\pi \right)=\tan\left(-\dfrac{7}{12}\pi \right) \]
Poi, notiamo che:
\[ -\dfrac{7}{12}\pi=-\dfrac{\pi}{3}-\dfrac{\pi}{4} \]
Gli angoli \( -\dfrac{\pi}{3} \) e \( -\dfrac{\pi}{4} \) sono notevoli e di essi conosciamo il valore della funzione tangente. Così, utilizzando la formula di addizione della tangente otteniamo:
\[ \begin{align}&\tan\left(\dfrac{5}{12}\pi \right)=\tan\left(-\dfrac{7}{12}\pi \right)=\tan \left(-\dfrac{\pi}{3}-\dfrac{\pi}{4} \right)= \\ \\ & = \dfrac{\tan\left( -\dfrac{\pi}{3}\right)+\tan\left(-\dfrac{\pi}{4} \right)}{1-\tan\left(-\dfrac{\pi}{3} \right)\tan \left(-\dfrac{\pi}{4} \right)}=\dfrac{-\sqrt{3}+(-1)}{1-[-\sqrt{3}\cdot(-1)]}= \\ \\ & = \dfrac{-\sqrt{3}-1}{1-\sqrt{3}} \cdot \dfrac{1+\sqrt{3}}{1+\sqrt{3}}= \dfrac{-2 \sqrt{3}-4}{-2}= \dfrac{-2(\sqrt{3}+2)}{-2} = \sqrt{3}+2\end{align} \]
Avremo così:
\[ \begin{align} c &= \tan \gamma\cdot b=\tan \left(\dfrac{5}{12} \pi\right)\cdot (\sqrt{6}-\sqrt{2})= \\ \\ &= (\sqrt{3}+2)\cdot(\sqrt{6}-\sqrt{2})=\sqrt{3}\cdot\sqrt{6}-\sqrt{3}\cdot\sqrt{2}+2 \sqrt{6}-2\sqrt{2}= \\ \\ & = \sqrt{3} \cdot \sqrt{3} \cdot \sqrt{2} – \sqrt{3}\sqrt{2}+2\sqrt{3}\sqrt{2}-2\sqrt{2}= \\ \\ & = \sqrt{2}(\sqrt{3}\sqrt{3}-\sqrt{3}+2\sqrt{3}-2)=\\ \\ & = \sqrt{2}(3-\sqrt{3}+2\sqrt{3}-2)=\sqrt{2}(1+\sqrt{3})=\sqrt{2}+\sqrt{2}\sqrt{3} = \\ \\ & = \sqrt{2}+\sqrt{6}\end{align} \]
L’esercizio termina qui.
Esercizio 5
Risolvere il seguente triangolo rettangolo:
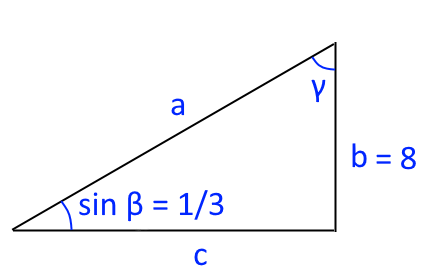
L’angolo in questo caso non ci viene fornito direttamente. Abbiamo piuttosto la valutazione della funzione seno in corrispondenza di tale angolo.
Applichiamo il primo teorema sui triangoli rettangoli:
\[ b = \sin \beta \cdot a \quad \Rightarrow \quad a = \dfrac{b}{\sin \beta} = \dfrac{8}{\dfrac{1}{3}}=8 \cdot 3 = 24 \]
Poi, utilizzando il teorema di Pitagora ricaviamo il cateto \( c \):
\[ \begin{align} c &= \sqrt{a^2-b^2}=\sqrt{24^2-8^2}=\sqrt{576-64}=\sqrt{512}=\sqrt{2 \cdot 2^8}= \\ \\ & = 2^4 \cdot \sqrt{2}=16 \sqrt{2}\end{align} \]
Può essere utile chiarire un passaggio relativo al termine \( \sqrt{512} \). Osserviamo che si ha:
\[ \begin{align}\sqrt{512}&=\sqrt{2^9}=\sqrt{2 \cdot 2^8}=\sqrt{2} \cdot \sqrt{2^8}=\sqrt{2} \cdot (2^8)^{\frac{1}{2}}= \\ \\ & =\sqrt{2}\cdot2^{8 \cdot \frac{1}{2}}=\sqrt{2}\cdot2^4=16 \sqrt{2} \end{align} \]
Così, l’operazione che nella pratica si effettua “portando fuori” il termine \( 2^8 \) dal simbolo di radice quadrata dimezzandone l’esponente non è altro che un’applicazione della proprietà delle potenze di potenze. E ricordiamo come ulteriore chiarimento dei passaggi effettuati che \( \sqrt{x}=x^{\frac{1}{2}} \).
Tornando al triangolo rettangolo da risolvere, ci rimane da ricavare \( \sin \gamma \). Come dato di partenza sugli angoli abbiamo, ricordiamo, \( \sin \beta = \dfrac{1}{3} \).
Osserviamo che si ha:
\[ \beta=90°-\gamma \]
E per gli archi associati:
\[ \sin(90°-\gamma) = \cos \gamma \]
e quindi:
\[ \cos \gamma = \dfrac{1}{3} \]
Ci rimane ora soltanto da utilizzare la relazione fondamentale della trigonometria. Per il nostro caso scriviamo:
\[ \sin \gamma = \sqrt{1-\cos^2 \gamma}=\sqrt{1-\dfrac{1}{9}}=\sqrt{\dfrac{8}{9}}=\dfrac{2 \sqrt{2}}{3} \]
L’esercizio è così concluso. Veniamo ora all’ultimo di questi esercizi sui triangoli rettangoli.
Esercizio 6
Risolvere un triangolo uguale a quello dell’esercizio precedente dati però \( b = 15 \) e \( \tan \beta = \dfrac{5}{24} \).
Ancora, l’angolo ci viene fornito non direttamente ma come valutazione di una funzione goniometrica. Poiché in particolare ci viene data la valutazione per tale angolo della funzione tangente, possiamo utilizzare il secondo teorema dei triangoli rettangoli. Si ha:
\[ b = \tan \beta \cdot c\quad \Rightarrow \quad c = \dfrac{b}{\tan \beta}=15 : \dfrac{5}{24}=15 \cdot \dfrac{24}{5}=72 \]
Avendo ora i due cateti, utilizzando il teorema di Pitagora possiamo ricavare l’ipotenusa:
\[ a = \sqrt{b^2+c^2}=\sqrt{15^2+72^2}=\sqrt{225+5184}=\sqrt{5409}=3\sqrt{601} \]
Ora, poiché:
\[ c = \sin \gamma \cdot a \]
utilizzando la formula inversa abbiamo in conclusione:
\[ \sin \gamma = \dfrac{c}{a}=\dfrac{72}{3\sqrt{601}}=\dfrac{24}{\sqrt{601}} \]
Qui termina questa serie di esercizi sui teoremi dei triangoli rettangoli. Nella prossima lezione vedremo il teorema della corda. Buono studio a tutti voi! 🙂
