Fra i concetti di universo, dominio e insieme di verità ce n’è uno del quale abbiamo già fatto conoscenza: l’insieme universo (detto universo per brevità). Se vi ricordate, di esso abbiamo parlato nell’ambito dell’insieme complementare. Quindi, vediamo come nella matematica gran parte degli argomenti sono tra loro collegati. Tanto più che nella prossima lezione, come vedrete, ritroveremo anche il concetto di insieme complementare 😉
Senza ulteriori indugi, cominciamo subito ad introdurre le definizioni di insieme universo, dominio e insieme di verità.
Insieme universo e insieme dominio. Insieme verità di una proposizione aperta
Consideriamo la proposizione (aperta):
\[ p(x): “\: x > 7 ” \]
cioè “\( x \) è maggiore di \( 7 \)”.
La proposizione ha senso in tutti i casi nei quali \( x \) è un numero. Cioè, una volta che alla \( x \) è stato attribuito un numero, è possibile chiedersi se tale numero è maggiore di \( 7 \) oppure no.
Diversamente, attribuendo alla \( x \) l’argomento “gatto”, non ha alcun senso chiedersi se “gatto è maggiore di 7”.
Esiste dunque un insieme costituito da elementi i quali sono tutti attribuibili alla \( x \)? La proposizione \( p(x) \) ha senso ad esempio per qualunque numero naturale. Diremo allora che l’insieme dei numeri naturali è un possibile insieme universo per la proposizione \( p (x)\).
Se però decidiamo di lavorare con i numeri razionali, cioè con tutti i numeri esprimibili come frazioni, allora diremo che l’insieme universo di \( p(x) \) è l’insieme dei numeri razionali. Anche esso è un possibile universo per \( p(x) \), poiché chiedersi se la proposizione \( p(x)\) è vera ha senso per un qualsiasi numero razionale.
NOTA: osserviamo che ogni numero intero è esprimibile come frazione (es, \( 2= \dfrac{2}{1} \)), per cui l’insieme dei numeri naturali è un sottoinsieme proprio dell’insieme dei numeri razionali 😉
Consideriamo adesso la proposizione:
\[ q(x): “\: \text{la somma di} \: 3 \text{ e} \: x \: \text{divisa per} \: x \: \text{e’ maggiore di 0}” \]
ovvero in simboli:
\[ q(x): “\dfrac{3+x}{x}>0” \]
Poiché non è possibile dividere per zero, la proposizione per \( x=0 \) perde di significato. Zero è comunque un numero, e quindi appartiene all’universo numerico fissato, tuttavia ci porta a compiere la divisione per zero, che è un’operazione non ammessa.
Diciamo allora che tale elemento “critico”, pur appartenendo all’insieme universo, non appartiene all’insieme dei valori per i quali si possono fare tutti i calcoli presenti nella proposizione. Per \( x=0 \) possiamo calcolare il termine \( 3+x \) , ma non possiamo dividere per \( x \).
Indichiamo come insieme dominio la differenza tra l’insieme universo e l’insieme dei valori per i quali non è possibile eseguire tutti i calcoli eventualmente presenti all’interno di una proposizione.
Così, per la proposizione \( q(x) \) il dominio è dato dall’insieme universo meno l’insieme costituito dall’elemento \( 0 \). Se indichiamo con \( D \) il dominio e \( U \) l’universo scelto, si ha:
\[ D=U\setminus \{0\} \]
Osserviamo invece che per la proposizione \( p(x) \) (ovvero “\( x > 7 \)”) non esistono valori dell’insieme universo “proibiti”. Valori, cioè, in corrispondenza dei quali si originano calcoli non permessi dalle regole della matematica. In questo caso, universo e dominio coincidono.
Quindi, avremo in generale:
\[ D \subseteq U \]
cioè il dominio è un sottoinsieme dell’insieme universo. Ovvero, \( D \) può essere un sottoinsieme proprio di \( U \) oppure può coincidere con esso.
NOTA: in molte fonti, i concetti di dominio e universo nel caso delle proposizioni vengono fatti coincidere. Se questo è l’approccio del vostro libro di testo o del vostro insegnante, è sufficiente che consideriate come insieme universo o dominio l’insieme che in questa lezione viene definito “dominio”. Personalmente ritengo comunque molto più ragionevole distinguere tra dominio e universo, anche come preparazione allo studio delle funzioni.
Una volta determinato il dominio della proposizione \( p(x) \), sarà possibile chiedersi qual’è l’insieme di verità della proposizione \( p(x) \), cioè individuare per quali valori \( x \) del dominio la proposizione \( p(x) \) è vera.
In altre parole, si prende un valore per la \( x \) dal dominio, si assegna tale valore a tutti gli argomenti variabili presenti nella proposizione, e infine si valuta se la proposizione è vera o falsa. Si ripete questo processo per ogni valore del dominio \( x \).
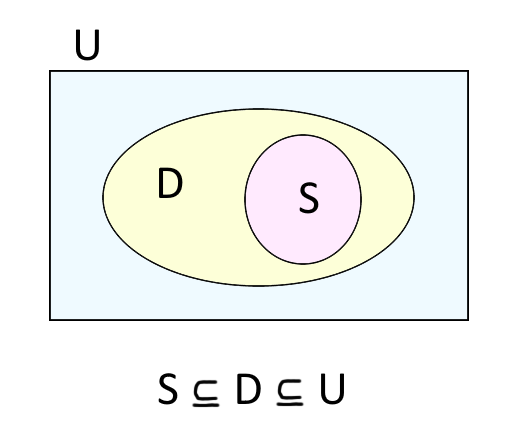
L’insieme di verità di una proposizione è l’insieme dei valori della variabile \( x \) per i quali la proposizione risulta vera.
Indicando con \( S \) l’insieme verità, si ha:
\[ S \subseteq D \subseteq U \]
cioè l’insieme di verità sarà generalmente un sottoinsieme proprio del dominio o al massimo potrà coincidere con il dominio stesso (non potrà mai comprendere elementi di \( U \) che non appartengono al dominio). Dunque, dobbiamo ricercare i valori della \( x \) che rendono vera la proposizione \( p(x) \) sempre e soltanto fra i valori del dominio.
Possiamo riassumere graficamente le definizioni introdotte come segue:
Esempi
ESEMPIO 1
Determinare l’insieme di verità della proposizione:
\[ p(x):\text{“il quadrato di} \: x \: \text{e’ maggiore o uguale a 0”} \]
Poiché non viene specificato l’insieme universo, sta a noi fissarlo. Consideriamo ad esempio i numeri relativi (cioè i numeri interi positivi e negativi, compreso lo zero). Sia quindi:
\[ U=\mathbb{Z} \]
Il quadrato è semplicemente l’operazione di moltiplicazione di un numero per sé stesso. E per come è definita l’operazione di moltiplicazione, è possibile moltiplicare tra loro una coppia di numeri qualsiasi. Di conseguenza, ogni elemento dell’insieme universo è anche elemento del dominio e si ha:
\[ D = \mathbb{Z} \]
Ora, poiché per le regole dell’algebra si ha che moltiplicando un numero negativo per un altro numero negativo si ha un risultato positivo, è chiaro che il quadrato di un numero negativo darà come risultato un numero positivo.
E’ ancora più chiaro del resto che il quadrato di un numero positivo sarà ancora un numero positivo.
E’ dunque comprensibile che per qualunque valore della \( x \) che prendiamo in \( \mathbb{Z} \), comunque la proposizione sarà vera.
Di conseguenza, abbiamo che:
\[ S=\mathbb{Z} \]
Abbiamo cioè per la proposizione data che insieme universo, insieme dominio e insieme di verità coincidono.
ESEMPIO 2
Ora, consideriamo la proposizione:
\[ q(x):”\{\text{la radice quadrata di }x\text{ e’ maggiore di 3}\}” \]
Per stabilire il valore di verità della proposizione, è sufficiente eseguire un calcolo. Per cui, l’insieme universo per la proposizione è sicuramente dato da un insieme numerico. Prendiamo \( U = \mathbb{R} \), cioè l’insieme dei numeri reali. Per intenderci, tale insieme contiene tutti i numeri positivi e negativi esprimibili come frazioni più i numeri aventi una parte decimale ma non esprimibili come frazioni (i cosiddetti numeri irrazionali).
Ora, se proviamo con una semplice calcolatrice a valutare la radice quadrata di -3, otteniamo un errore. Infatti, non è possibile (almeno con i numeri reali) calcolare la radice quadrata di numeri negativi.
Quindi, sebbene la proposizione sia ben posta per gli insiemi numerici, cioè abbia senso provare a fare il calcolo per ogni numero reale, esistono numeri reali che ci indirizzano verso operazioni matematiche non consentite. Perciò, il dominio della proposizione \( q(x) \) è dato soltanto dai numeri reali positivi (compreso lo zero poiché la radice quadrata di zero si può fare).
Quindi, per \( q(x) \), fissato \( U = \mathbb{R} \), sarà:
\[ D=\{x \in \mathbb{R} \quad \text{t.c.} \quad x \geq 0\} \]
Come vedete, abbiamo ritrovato esattamente il concetto di insieme universo che avevamo definito per gli insiemi 😉 E il dominio della proposizione rappresenta in questo caso un sottoinsieme proprio dell’insieme universo:
\[ D \subset U \]
Ora che conosciamo il dominio, ci rimane da determinare l’insieme di verità \( S \) della proposizione, cioè l’insieme dei valori \( x \) del dominio per i quali la proposizione è vera.
Si tratta di risolvere la disequazione:
\[ \sqrt{x}>3 \]
Ora, vedremo più avanti che la disequazione è verificata per \( x>9 \) (basta fare il quadrato della \( x \) e del \( 3 \)). Quindi l’insieme di verità \( S \) della proposizione (che corrisponde all’insieme delle soluzioni della disequazione) è pari a:
\[ S =\{x \in \mathbb{R} \quad \text{t.c.} \quad x>9\} \]
Vediamo dunque come in questo caso:
\[ S \subset D \subset \mathbb{R} \]
cioè abbiamo che il dominio è un sottoinsieme proprio dell’insieme universo (a causa della presenza della radice quadrata nella proposizione) e che l’insieme delle soluzioni è un sottoinsieme proprio del dominio (a causa della condizione “è maggiore di 3” presente nella proposizione).
Siamo dunque arrivati alla fine di questa lezione sui concetti di Universo, dominio e insieme di verità. Nella prossima lezione, finalmente, cominceremo a fare la conoscenza dei connettivi logici (noti anche come operatori logici), e vedremo le corrispondenti operazioni logiche. Buono studio a tutti! 🙂
