In particolare, cominciamo ipotizzando di conoscere i valori di verità dell’implicazione \( a \rightarrow b \) e di una delle due proposizioni. Con queste informazioni, vogliamo vedere se e quando riusciamo a determinare il valore di verità dell’altra proposizione. Il risultato sarà che potremo farlo in due casi, ottenendo quindi le due regole di inferenza modus ponens e modus tollens.
Ricavare le regole di inferenza modus ponens e modus tollens
Supponiamo di sapere già che l’implicazione \( a \rightarrow b \) è vera, e supponiamo anche di conoscere il valore di verità di una delle due proposizioni. Potremo quindi avere quattro distinti casi:
- \( a \rightarrow b \) è vera e la proposizione \( a \) è vera;
- \( a \rightarrow b \) è vera e la proposizione \( b \) è vera;
- \( a \rightarrow b \) è vera e la proposizione \( a \) è falsa;
- \( a \rightarrow b \) è vera e la proposizione \( b \) è falsa.
Ora, a partire da questi dati, riusciamo in ciascun caso a determinare il valore di verità della proposizione il cui valore di verità non è noto?
PRIMO CASO
Come dati di partenza, abbiamo che l’implicazione \( a \rightarrow b \) è vera e che la proposizione \( a \) è vera. Da questi dati riusciamo a ricavare il valore di verità della proposizione \( b? \)
Il punto di partenza è la tavola di verità dell’implicazione. Vediamo quando si verifica contemporaneamente che l’implicazione \( \: a \rightarrow b \) è vera e che la proposizione \( a \) è vera.
Primo caso: modus ponens

Come possiamo vedere, questa eventualità si verifica unicamente nella prima riga della tavola della verità.
Possiamo quindi concludere che se l’implicazione \( a \rightarrow b \) è vera e la proposizione \( a \) è vera, allora la proposizione \( b \) è vera.
Questa conclusione costituisce una regola di inferenza chiamata modus ponens.
SECONDO CASO
Ipotizziamo ora di sapere che l’implicazione \( a \rightarrow b \) è vera e che la proposizione \( b \) è vera. Possiamo dire qualcosa sul valore di verità della proposizione \( a \)? Allo stesso modo di prima, diamo uno sguardo alla tavola di verità dell’implicazione materiale 🙂
Secondo caso: nessuna regola possibile

Osserviamo che l’implicazione e la proposizione \( b \) sono entrambe vere in due differenti casi. In un caso, la proposizione \( a \) è vera, nell’altro la proposizione \( a \) è falsa. Di conseguenza, non possiamo dire nulla sul valore di verità della proposizione \( a \).
TERZO CASO
Ora, ipotizziamo che l’implicazione sia vera e che la proposizione \( a \) sia falsa. Consultiamo la tavola di verità per capire quando si verifica questa eventualità. Possiamo trarre conclusioni sul valore di verità della proposizione \( b \)?
Terzo caso: nessuna regola possibile

Come possiamo vedere, nella terza riga la proposizione \( b \) risulta vera, mentre nella quarta riga la proposizione \( b \) risulta falsa. Dunque, se l’implicazione è vera e se la proposizione \( a \) è falsa, non possiamo dire nulla sul valore di verità della proposizione \( b \).
Quarto caso: modus tollens
Veniamo ora al quarto ed ultimo caso. Ipotizziamo ora che l’implicazione sia, come al solito vera, e che la proposizione \( b \) sia falsa. Possiamo dire qualcosa per la proposizione \( a \)?
Ancora una volta, diamo uno sguardo alla tavola di verità dell’implicazione materiale e controlliamo quando succede che l’implicazione \( a \rightarrow b \) è vera e allo stesso tempo la proposizione \( b \) è falsa.
Quarto caso: modus tollens
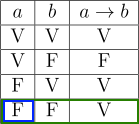
Osserviamo che questa circostanza si verifica in un solo caso. Di conseguenza, possiamo affermare che se \( a \rightarrow b \) è vera e la proposizione \( b \) è falsa, allora la proposizione \( a \) è falsa.
Questa conclusione costituisce una regola di inferenza chiamata modus tollens.
Vediamo ora un paio di esempi di utilizzo delle regole di inferenza che abbiamo ricavato.
Modus ponens (esempio)
Sia data l’implicazione:
\( a \rightarrow b \): “Se suono la batteria sono un batterista”
Osserviamo anzitutto che essa è costituita da due proposizioni:
\( a \): “Suono la batteria”
\( b \): “Sono un batterista”
Ora, supponiamo di sapere soltanto che l’implicazione è vera e che la proposizione \( a \) è vera. Abbiamo quindi i dati di partenza:
\( a \rightarrow b \): “Se suono la batteria sono un batterista” (vera)
\( a \): “Suono la batteria” (vera)
Applicando la regola del modus ponens, possiamo concludere che:
\( b \): “Sono un batterista”
è una proposizione vera. Quindi, otteniamo il ragionamento: “Se chi suona la batteria è un batterista, e io suono la batteria, allora io sono un batterista”.
Modus tollens (esempio)
Riprendiamo la stessa implicazione dell’esempio precedente.
Ora, supponiamo di sapere soltanto che l’implicazione è vera e che la proposizione \(b \) è falsa. Abbiamo quindi i dati di partenza:
\( a \rightarrow b \): “Se suono la batteria sono un batterista” (vera)
\( b \): “Sono un batterista” (falsa)
Applicando la regola del modus tollens, possiamo concludere che anche la proposizione \( a \) è falsa:
\( a \):”Suono la batteria” (falsa)
Negando le proposizioni che sono non vere, otteniamo il seguente ragionamento, in cui l’implicazione e tutte le proposizioni sono vere:
\( a \rightarrow b \): “Se suono la batteria sono un batterista” (vera)
\( \overline{b} \): “Non sono un batterista” (vera)
Conclusione:
\( \overline{a} \): “Non suono la batteria” (vera)
Abbiamo riespresso il ragionamento in quest’ultima forma sfruttando il fatto che se una proposizione è falsa la sua negata è vera 😉
Osserviamo che la regola del modus tollens è anche detta regola della contronominale. Infatti, grazie alla negazione abbiamo ottenuto come conclusione il ragionamento “Non sono un batterista, allora non suono la batteria”. Se ci fate caso, questa è proprio l’implicazione
\[ \overline{b} \rightarrow \overline{a} \]
cioè, la contronominale (o controinversa). E come sappiamo, se è vera un’implicazione è vera anche la sua contronominale 😉
Qui finisce la lezione sulle regole di inferenza. Nella prossima lezione, vedremo i quantificatori. Ciao a tutti e buono studio con Altramatica! 🙂
