Il termine “implicazione” richiama in generale il concetto che da un fatto ne consegue un altro. L’implicazione materiale però usa un approccio differente rispetto al nostro modo comune di ragionare. In particolare, con l’implicazione materiale otteniamo, a partire da due proposizioni, una proposizione il cui valore di verità è definito da una tavola di verità. E la tavola di verità tiene conto unicamente del valore di verità delle singole proposizioni, e non necessariamente del nostro modo di pensare quotidiano.
In altre parole, l’implicazione materiale pone in relazione delle proposizioni a prescindere dal loro significato. E a noi spetta solo attribuire il risultato di vero o falso seguendo la tavola di verità. Ovviamente, con una scelta mirata delle proposizioni, l’implicazione materiale permette anche di costruire proposizioni molecolari che riflettono un ragionamento.
Definizione di implicazione materiale
Premettiamo anzitutto che utilizzeremo l’implicazione materiale con proposizioni chiuse. Lavoreremo con le proposizioni aperte in una prossima lezione introducendo l’implicazione logica.
Date due proposizioni chiuse \( a \) e \( b \), l’operazione di implicazione materiale tra le due proposizioni si indica con la scrittura:
\[ a \rightarrow b \]
e si legge “\( a \) implica \( b \)”, oppure “se \( a \) allora \( b \)”.
La proposizione \( a \) viene indicata col nome di premessa, la proposizione \( b \) con il nome di conseguenza.
L’operatore di implicazione \( \rightarrow \) è un operatore che collega tra loro due proposizioni. Il risultato che si ottiene dall’operazione corrispondente è una proposizione molecolare (cioè con almeno due predicati) il cui valore dipende dalla seguente tavola di verità:
Tavola di verità dell’implicazione materiale
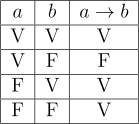
Consideriamo ad esempio le proposizioni:
a:”8 è maggiore di zero”
b: “8 è un numero positivo”
L’operazione di implicazione materiale \( a \rightarrow b \) ci permette di costruire la proposizione seguente:
\( a \rightarrow b \): “Se 8 è maggiore di zero allora 8 è un numero positivo”
L’implicazione è vera poiché entrambe le proposizioni \( a \) e \( b \) sono vere (prima riga della tavola di verità).
Ora, la proposizione che abbiamo ottenuto effettivamente ha un chiaro significato, tuttavia dobbiamo sempre ragionare soltanto sul valore di verità delle singole proposizioni che compongono l’implicazione. L’implicazione materiale sarà vera o falsa solo in base ad esse 😉
Consideriamo infatti le seguenti proposizioni:
a: “L’elefante è un animale”
b: “Roma è la capitale d’Italia”
L’implicazione \( a \rightarrow b \):
\( a \rightarrow b \): “Se l’elefante è un animale allora Roma è la capitale d’Italia”
è vera poiché entrambe le proposizioni sono vere. Per concludere questo, semplicemente guardiamo cosa ci dice la tabella di verità nel caso in cui entrambe le proposizioni sono vere. Non dobbiamo fare alcun ragionamento in più 😉
Ora, mi sembra chiaro che l’evidenza che l’elefante sia un animale non c’entri assolutamente nulla col fatto che Roma sia la capitale del nostro paese. Quindi, è naturale che uno si domandi di cosa ci stiamo occupando 😉
L’idea è quella che l’implicazione materiale collega materialmente due proposizioni tra loro, senza prestare attenzione al loro significato. Diciamo che questa operazione rappresenta uno strumento per provare a costruire dei ragionamenti. Poi, come detto, il fatto di ottenere una proposizione che abbia senso o meno dipende unicamente dalle proposizioni sulle quali operiamo.
Facciamo ancora un esempio. Consideriamo le due proposizioni:
a: “2 è un numero maggiore di 10”
b: “8 è un numero pari”
Effettuando l’operazione di implicazione materiale tra le due proposizioni otteniamo:
\( a \rightarrow b \): “Se 2 è un numero maggiore di 10 allora 8 è un numero pari”
Tale implicazione è vera poiché la premessa (proposizione \( a \)) è falsa ma la conseguenza (proposizione \( b \)) è vera. Siamo nel caso della terza riga della tavola di verità.
Ancora una volta, riusciamo ad attribuire un valore di verità alla implicazione soltanto utilizzando la tavola di verità. Diversamente, dal punto di vista del significato l’implicazione costruita non ha alcun senso.
Proprietà dell’implicazione materiale
Osserviamo con attenzione la seconda e la terza riga della tavola di verità dell’implicazione materiale. Possiamo concludere agevolmente che l’implicazione materiale non ha la proprietà commutativa.
Infatti, possiamo vedere che, per la tavola di verità, è vero che una proposizione falsa implica una proposizione vera (terza riga) ma non è vero che una proposizione vera implica una proposizione falsa (seconda riga).
In altre parole, data l’implicazione diretta:
\[ a \rightarrow b \]
la sua contraria:
\[ b \rightarrow a \]
può avere valore di verità opposto all’implicazione diretta (cioè l’implicazione \( a \rightarrow b \)).
Detta in un altro modo, se è vera \( a \rightarrow b \), non possiamo concludere che è anche vera \( b \rightarrow a \).
Invece, utilizzando l’operazione di negazione logica su entrambe le proposizioni, possiamo dire che se \( a \rightarrow b \) è vera, allora è anche vera l’implicazione \( \overline{b} \rightarrow \overline{a} \). Inoltre, se \( a \rightarrow b \) è falsa, anche l’implicazione \( \overline{b} \rightarrow \overline{a} \) è falsa. Queste proprietà sono verificabili in modo immediato utilizzando la tavola di verità 😉
Quindi, possiamo dire che la proposizione \( \overline{b} \rightarrow \overline{a} \), detta contronominale o anche controinversa, ha lo stesso valore di verità di \( a \rightarrow b \).
Esempio
Consideriamo le seguenti proposizioni:
\( a: \)”Il rubinetto è aperto”
\( b \):”L’acqua esce dal rubinetto”
Le proposizioni sono ben poste poiché è sempre possibile controllarne il valore di verità. E’ sufficiente controllare rispettivamente se il rubinetto è aperto o chiuso oppure se l’acqua esce dal rubinetto o meno.
Si tratta di proposizioni chiuse poiché gli argomenti sono specificati (non abbiamo variabili \( x \)). Tuttavia, il valore di verità può cambiare nel tempo (ad esempio, in un dato momento il rubinetto può essere chiuso, in un dato momento può essere aperto). Diversamente, una proposizione del tipo “\( 5 \) è maggiore di \( 2 \)” è sempre falsa. Il suo valore di verità non cambierà mai.
Quindi, per attribuire in questo caso un valore di verità alle singole proposizioni, dovremo guardare cosa succede in un dato istante di tempo. Poi, attribuiremo il valore di verità alla proposizione costruita con l’implicazione secondo quanto dettato dalla tavola di verità dell’implicazione materiale.
Costruiamo l’implicazione materiale \( a \rightarrow b \):
\( a \rightarrow b \): “Se il rubinetto è aperto l’acqua esce dal rubinetto”
Se entrambe le proposizioni sono vere (cioè ipotizziamo che in un dato istante il rubinetto è aperto e esce l’acqua dal rubinetto), dalla tavola di verità risulta che l’implicazione è vera.
Proviamo a costruire la controinversa:
\( \overline{b} \rightarrow \overline{a} \): “Se non è vero che il rubinetto è aperto, allora non è vero che l’acqua esce dal rubinetto”
Poiché consideriamo l’istante di tempo nel quale il rubinetto è aperto e esce l’acqua, possiamo affermare che entrambe le proposizioni sono false. Allora, l’implicazione, come dalla tavola di verità, risulta vera.
In questo caso, otteniamo un ragionamento sensato (la controinversa praticamente è: “se il rubinetto è chiuso, l’acqua non esce dal rubinetto”). Osserviamo però che pur avendo utilizzato due proposizioni collegate tra loro logicamente, continuiamo imperterriti a decidere il valore di verità dell’implicazione semplicemente mediante la tavola di verità 😉 Questo infatti è il modo di operare con l’implicazione materiale.
Ora, la particolare implicazione materiale costruita è anche un’implicazione logica, poiché è possibile dimostrare scientificamente il rapporto causa-effetto tra l’apertura del rubinetto e la conseguente uscita di acqua dallo stesso. Questo è conseguenza del fatto che abbiamo scelto di lavorare su proposizioni collegate fra loro secondo un nesso causa-effetto. E come possiamo vedere, la tavola di verità dell’implicazione materiale ci ha permesso di descrivere secondo le sue regole degli eventi che hanno un riscontro anche nella realtà 😉
Qui termina questa lezione sull’implicazione materiale. Nella prossima lezione vedremo la coimplicazione materiale. Buono studio a tutti! 🙂
