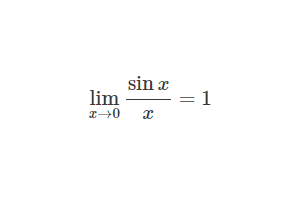L’idea è quella di ricercare nel limite da risolvere la struttura di uno dei limiti notevoli e risolvere l’esercizio di conseguenza. Come non calcoliamo ogni volta i prodotti notevoli nei polinomi, allo stesso modo non calcoliamo ogni volta i limiti notevoli nei limiti 😉
In questa lezione vedremo cosa sono i limiti notevoli e forniremo un elenco di quelli principali. Per chi conosce già l’argomento e desidera una tabella sintetica e completa, è disponibile questa ulteriore risorsa 😉
Nella successiva lezione ci occuperemo dell’utilizzo dei limiti notevoli, introducendo un primo elementare metodo (metodo algebrico).
Se siete già a conoscenza dell’argomento trattato in questa lezione e siete invece alla ricerca dei limiti notevoli “generalizzati”, cioè espressi in \( f(x) \), è per voi disponibile questa tabella. Per chi invece desidera sapere come si ricavano i principali limiti notevoli, è disponibile questa lezione.
Tabella dei limiti notevoli
Vediamo prima di tutto un elenco dei limiti notevoli principali nella variabile \( x \). Seguiranno poi esempi ed osservazioni.
Osserviamo che i limiti notevoli ci consentono di svincolarci da particolari forme indeterminate. Nello specifico, il limite notevole del numero di Nepero si riferisce alla forma indeterminata \( 1^{\infty} \). Tutti gli altri limiti notevoli invece ci consentono di liberarci della forma indeterminata \( \left[\dfrac{0}{0}\right] \).
Una tabella completa di tutti i limiti notevoli nella forma in \( x \) e in \( f(x) \) è disponibile qui.
Limite notevole della funzione esponenziale con base a
\[ \lim_{x \to 0}\dfrac{a^{x}-1}{x}=\ln a,\qquad a > 0 \]
Nel caso di base \( e \):
\[ \lim_{x \to 0}\dfrac{e^x-1}{x}=1 \]
Limite notevole della funzione logaritmica con base a
\[ \lim_{x \to 0}\dfrac{\log_a(1+x)}{x}=\dfrac{1}{\ln a } \qquad a>0, \quad a \neq 1 \]
Nel caso del logaritmo naturale (cioè il logaritmo in base \( e \)):
\[ \lim_{x \to 0} \dfrac{\ln(1+x)}{x}=1 \]
Limite notevole del numero di Nepero
Il numero di Nepero, ossia \( e \), può essere ottenuto come risultato del limite:
\[ \lim_{x \to \pm \infty}\left(1+\dfrac{1}{x} \right)^x=e \]
Limite notevole del seno
\[ \lim_{x \to 0} \dfrac{\sin x}{x}=1 \]
Limite notevole del coseno
\[ \lim_{x \to 0} \dfrac{1-\cos x}{x^2}=\dfrac{1}{2} \]
Limite notevole della tangente
\[ \lim_{x \to 0} \dfrac{\tan(x)}{x}=1 \]
Limite notevole della potenza con differenza
\[ \lim_{x \to 0}\dfrac{(1+x)^k-1}{x}=k, \qquad k \in \mathbb{R} \]
Riportiamo infine i limiti notevoli di alcune funzioni trigonometriche inverse.
Limite notevole della funzione arcoseno
\[ \lim_{x \to 0}\dfrac{\arcsin x}{x}=1 \]
Limite notevole della funzione arcotangente
\[ \lim_{x \to 0} \dfrac{\arctan x}{x}=1 \]
Prime osservazioni sul corretto uso dei limiti notevoli
E’ fin da subito importante prestare attenzione a quale valore tende la \( x \) nei limiti. Ad esempio, nel limite notevole del seno:
\[ \lim_{x \to 0}\dfrac{\sin x}{x}=1 \]
la \( x \) tende a 0, mentre nel limite notevole del numero di Nepero:
\[ \lim_{x \to \pm \infty}\left(1+\dfrac{1}{x} \right)^x=e \]
la \( x \) tende a più infinito oppure a \( -\infty \).
Prima di usare un limite notevole per risolvere un esercizio, è di fondamentale importanza confrontare il valore al quale tende la \( x \) nel limite notevole con il valore al quale tende la \( x \) nell’esercizio. I due valori devono essere uguali! 🙂
Ad esempio, supponiamo di dover risolvere il seguente limite:
\[ \lim_{x \to +\infty}5 \dfrac{\sin x}{x} \]
Possiamo intanto portare fuori il termine costante dal segno di limite (vedi teorema del limite del prodotto di funzioni):
\[ \lim_{x \to +\infty}5 \dfrac{\sin x}{x}= 5\lim_{x \to +\infty}\dfrac{\sin x}{x} \]
Riconosciamo agevolmente lo stesso argomento del limite notevole del seno ma attenzione! Nell’esercizio la \( x \) tende a più infinito, mentre nel limite notevole la \( x \) tende a 0! Quindi, nonostante la somiglianza presente, in realtà il limite notevole del seno non ci è di alcun aiuto per risolvere l’esercizio! Usarlo sarebbe un errore grave. Dunque, non possiamo risolvere l’esercizio con i limiti notevoli.
Possiamo invece risolvere agevolmente quest’altro esercizio:
\[ \lim_{x \to 0}5 \dfrac{\sin x}{x} \]
Ora infatti la \( x \) tende a zero sia nell’esercizio, sia nel limite notevole. Possiamo pertanto sfruttare tranquillamente l’informazione fornita dal limite notevole del seno. Quindi:
\[ \lim_{x \to 0}5 \dfrac{\sin x}{x}=5 \cdot \lim_{x \to 0}\dfrac{\sin x}{x}=5 \cdot 1 = 5 \]
Vi ricordo che è anche disponibile in Altramatica una tabella riassuntiva completa di tutti i limiti notevoli.
Teorema del limite della potenza di una funzione e limiti notevoli
Facciamo ora un’importante osservazione. Sapendo che:
\[ \lim_{x \to 0}\dfrac{\sin x}{x}=1 \]
possiamo anche dire che:
\[ \lim_{x \to 0}\dfrac{x}{\sin x}=1 \]
Ciò è conseguenza del teorema del limite della potenza di una funzione: il limite della potenza di una funzione equivale alla potenza del limite della funzione stessa. Nel caso in cui l’esponente sia pari a -1 abbiamo infatti:
\[ \quad \lim_{x \to 0}\left(\dfrac{\sin x}{x} \right)^{-1}=\left(\lim_{x \to 0}\dfrac{\sin x}{x} \right)^{-1} \]
e siccome \( \left( \dfrac{\sin x}{x} \right)^{-1}=\dfrac{x}{\sin x} \) e poiché come noto \( \lim_{x \to 0}\dfrac{\sin x}{x}=1 \) si ha in conclusione:
\[ \lim_{x \to 0}\dfrac{x}{\sin x}=1 \]
Tale osservazione si può fare in modo del tutto simile per tutti quei limiti notevoli che sono espressi come rapporto di funzioni.
Quindi, come ulteriore esempio, dal limite notevole:
\[ \lim_{x \to 0} \dfrac{1-\cos x}{x^2}=\dfrac{1}{2} \]
deduciamo anche l’informazione:
\[ \lim_{x \to 0} \dfrac{x^2}{1-\cos x}=2 \]
cioè, in generale, per i limiti notevoli nei quali si ha un rapporto tra funzioni, possiamo dire che il limite del reciproco del rapporto delle funzioni equivale al reciproco del limite.
Questo è molto importante da tenere conto per la risoluzione degli esercizi. Spesso infatti, lavorando con l’algebra sull’argomento del limite da risolvere, ci ritroviamo con rapporti tra funzioni che sono proprio i reciproci di quelli che compaiono nel limite notevole considerato 😉
Nella prossima lezione, vedremo il metodo algebrico per la risoluzione dei limiti di funzioni con i limiti notevoli.
Ciao a tutti e, come sempre, buono studio con Altramatica!