Abbiamo visto nelle precedenti lezioni l’implicazione materiale e sappiamo che questa opera con una tavola di verità. Noti i valori di verità delle singole proposizioni, il valore di verità della proposizione \( a \rightarrow b \) si ottiene dalla tavola. E il valore di verità dell’implicazione materiale dipende soltanto dai valori di verità delle singole proposizioni.
Ora, con l’implicazione logica il discorso cambia. Assegnata un’implicazione logica, infatti, non possiamo stabilirne immediatamente il valore di verità utilizzando una tavola della verità. Piuttosto, sta a noi dimostrare che vi sia una connessione logica tra le due proposizioni che compongono la possibile implicazione logica.
Dalla implicazione materiale alla implicazione logica
Finora abbiamo lavorato con l’implicazione materiale considerando soltanto proposizioni chiuse, cioè proposizioni nelle quali gli argomenti sono fissati. Vediamo ora di estendere l’utilizzo dell’implicazione materiale al caso delle proposizioni aperte. Ricordiamo, nelle proposizioni aperte gli argomenti non sono più fissi ma dipendono dalla variabile \( x \).
Immaginiamo quindi di avere due proposizioni \( a(x) \) e \( b(x) \), entrambe definite in un insieme dominio \( D \). Sia \( S_1\subseteq D \) l’insieme di verità della proposizione \( a(x) \). Per ogni \( x \) che appartiene all’insieme \( S_1 \), sarà possibile valutare il valore di verità dell’implicazione materiale:
\[ a(x) \rightarrow b(x) \]
semplicemente utilizzando la tavola di verità.
Ora, se riusciamo a verificare che per un qualsiasi \( x \) dell’insieme \( S_1 \) il valore di verità dell’implicazione è sempre vero, allora possiamo affermare che la proposizione \( a(x) \) implica logicamente la proposizione \( b(x) \) nell’insieme \( S_1 \):
\[ a(x) \Rightarrow b(x) \qquad (\forall x \in S_1) \]
L’implicazione logica viene indicata con il simbolo \( \Rightarrow \).
In altre parole, se si verifica una tale circostanza, vuol dire che per ogni valore \( x \) dell’insieme \( S_1 \), dalla verità della proposizione \( a(x) \) si ha come conseguenza anche la verità della proposizione \( b(x) \).
Se l’insieme \( S_1 \) è chiaro dal contesto, si può semplicemente scrivere:
\[ a(x) \Rightarrow b(x) \]
e con tale scrittura si intende che ogni valore \( x \) che verifica \( a(x) \), verifica anche \( b(x) \).
Ovviamente, nella pratica non è generalmente possibile dimostrare un’implicazione logica verificando che l’implicazione materiale \( a(x) \rightarrow b(x) \) è vera per ogni \( x \) dell’insieme \( S_1 \). Basta pensare al caso in cui l’insieme \( S_1 \) sia costituito da infiniti elementi.
Sarà allora necessario dimostrare che \( a(x) \) implica logicamente \( b(x) \) mediante un’opportuna tecnica chiamata dimostrazione. Se si riesce a dimostrare tale implicazione logica, allora diremo che l’implicazione:
\[ a(x) \Rightarrow b(x) \]
costituisce un teorema.
Condizioni necessaria e sufficiente
Se dunque in un dato dominio è valida l’implicazione logica:
\[ a(x) \Rightarrow b(x) \]
diremo che \( a(x) \) è condizione sufficiente per \( b(x) \) per ogni \( x \) del dominio. In altri termini, per poter affermare che \( b(x) \) è vera in un dato \( x \) basta sapere che \( a(x) \) è vera. Ovvero, a partire dalla verità di \( a(x) \) si può dire che è vera anche \( b(x) \).
Inoltre, sempre se è valevole l’implicazione logica \( a(x) \Rightarrow b(x) \), diremo che \( b(x) \) è condizione necessaria per \( a(x) \). In altri termini, diremo che per poter avere la possibilità che in un dato \( x \) la proposizione \( a(x) \) è vera, dovrà essere per forza che per quello stesso \( x \) anche la proposizione \( b(x) \) è vera. E per quanto abbiamo detto, ciò dovrà ovviamente valere per ogni \( x \) dell’insieme di verità della proposizione \( a(x) \).
Ora, attenzione! 🙂 Se sappiamo che sussiste l’implicazione logica \( a(x) \Rightarrow b(x) \) e sappiamo che \( b(x) \) è vera, non possiamo direttamente concludere che \( b(x) \Rightarrow a(x) \)!
La proposizione \( b(x) \) non è condizione sufficiente per \( a(x) \), ma soltanto necessaria. In altre parole, la verità di \( b(x) \) è solo un prerequisito per la verità di \( a(x) \). Se \( b(x) \) non è vera, allora è possibile affermare con certezza che anche \( a(x) \) non è vera. Ma è bene ribadirlo: se \( b(x) \) è vera, non possiamo concludere nulla con questa sola informazione sulla proposizione \( a(x) \). L’implicazione \( b(x) \Rightarrow a(x) \) è dunque un’altra implicazione logica che deve essere dimostrata a parte.
Mancata sussistenza di un’implicazione logica
Un’implicazione logica \( a(x) \Rightarrow b(x) \) risulta falsa (nell’insieme \( S_1 \)) se esiste almeno un valore \( x \) nell’insieme \( S_1 \) per il quale si ha che la proposizione \( a(x) \) è vera e la proposizione \( b(x) \) è falsa.
Ciò è intuitivo, poiché se per uno stesso \( x \) la proposizione \( a(x) \) è vera e \( b(x) \) è falsa, allora è impossibile che la verità di \( a(x) \) implichi la verità di \( b(x) \).
Ora, come sappiamo la validità di un’implicazione logica si ottiene se e solo se l’implicazione materiale \( a(x) \rightarrow b(x) \) è vera per ogni \( x \) dell’insieme \( S_1 \).
Quindi, l’implicazione logica \( a(x) \Rightarrow b(x) \) risulterà falsa se esiste almeno un \( x \) dell’insieme \( S_1 \) per cui l’implicazione materiale \( a(x) \rightarrow b(x) \) è falsa.
Osservando la tavola di verità dell’implicazione materiale notiamo che l’implicazione materiale è falsa soltanto quando \( a(x) \) è vera e \( b(x) \) è falsa. Ritroviamo allora quanto detto: se esiste almeno un valore della \( x \in S_1 \) per cui \( a(x) \) è vera e \( b(x) \) è falsa, l’implicazione logica \( a(x) \Rightarrow b(x) \) non sussiste, cioè non è valida.
Se l’implicazione \( a(x) \Rightarrow b(x) \) non è verificata, allora possiamo dire che \( a(x) \) non è condizione sufficiente per \( b(x) \).
Esempio
Siano date le proposizioni:
\( a(x) \): “\( x \) è un multiplo di \( 9 \)”
\( b(x) \): “\( x \) è un multiplo di \( 3 \)”
definite ad esempio nel dominio \( D= \mathbb{N} \), cioè l’insieme dei numeri naturali. Sia \( S_1 \subseteq D \) l’insieme di verità della proposizione \( a(x) \).
Ci domandiamo se l’implicazione logica:
\[ a(x) \Rightarrow b(x) \]
è vera per ogni \( x \) dell’insieme \( S_1 \).
Ciò equivale a domandarci se per ogni valore \( x \) dell’insieme di verità della proposizione \( a(x) \) l’implicazione materiale:
\[ a(x) \rightarrow b(x) \]
risulta vera.
Ora, è possibile dimostrare che ogni numero multiplo di \( 9 \) è anche multiplo di \( 3 \). Il concetto del resto è intuitivo e basta provare con qualche numero per convincersene. Serve comunque una dimostrazione rigorosa, ma ora non è questo che ci interessa 😉
Dunque, non succede mai che se \( a(x) \) è vera, \( b(x) \) è falsa. L’implicazione materiale \( a(x) \rightarrow b(x) \) risulta cioè vera per ogni \( x \in S_1 \).
Possiamo dunque concludere che vale per ogni elemento dell’insieme \( S_1 \) l’implicazione logica:
\[ a(x) \Rightarrow b(x) \]
ovvero:
\[ a(x):”x \: \text{e’ multiplo di} \: 9″ \quad \Rightarrow \quad “x \: \text{e’ multiplo di }3” \]
Rappresentazione con gli insiemi dell’implicazione logica
Indichiamo con \( S_1 \) l’insieme di verità della proposizione \( a(x) \) e con \( S_2 \) l’insieme di verità della proposizione \( b(x) \).
Se sussiste l’implicazione logica
\[ a(x) \Rightarrow b(x) \]
si ha come conseguenza che l’insieme di verità della proposizione \( a(x) \) è un sottoinsieme dell’insieme di verità della proposizione \( b(x) \). In simboli:
\[ S_1 \subseteq S_2 \]
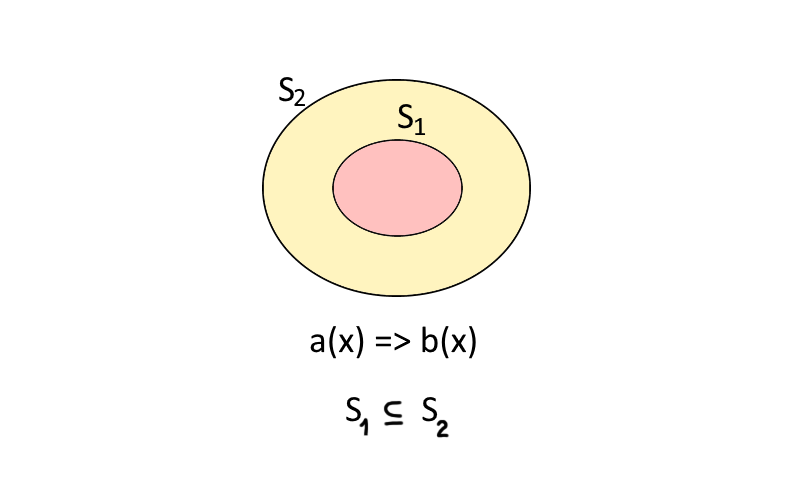
Infatti, sappiamo che \( a(x) \) è condizione sufficiente per \( b(x) \). Dunque, se un elemento \( x \) appartiene all’insieme di verità \( S_1 \), allora appartiene sicuramente anche all’insieme \( S_2 \). Dunque, per la definizione di inclusione tra insiemi, \( S_1 \) è incluso in \( S_2 \) poiché tutti i suoi elementi appartengono ad \( S_2 \).
Sappiamo anche però che se un elemento \( x \) rende vera la proposizione \( b(x) \), non possiamo concludere direttamente che tale elemento rende vera la proposizione \( a(x) \). Quindi, come detto, la verità di \( b(x) \) è condizione soltanto necessaria per la verità di \( a(x) \). Dal punto di vista degli insiemi di verità delle proposizioni, ciò significa che se un elemento appartiene all’insieme di verità \( S_2 \), non sappiamo dire se questo elemento appartiene anche all’insieme di verità \( S_1 \). In generale quindi, se un elemento appartiene ad \( S_2 \), questo può appartenere ad \( S_1 \) o anche non appartenervi.
Queste riflessioni giustificano la relazione di inclusione scritta tra gli insiemi \( S_1 \) ed \( S_2 \).
Per l’implicazione logica direi che è tutto. Nella prossima lezione vedremo la coimplicazione logica. Non perdetevela! 😉
