Retta tangente ad una curva dello spazio in un punto

 - 

Vettori (università)

Vediamo di introdurre la definizione di retta tangente ad una curva dello spazio in un punto, parametrizzata da un’opportuna funzione vettoriale. Con lo studio di tale definizione avremo anche modo di chiarire il significato geometrico della derivata in un punto di una funzione vettoriale.

Proseguiamo così lo studio delle funzioni vettoriali mostrando come si parametrizza la retta tangente ad una curva parametrica nello spazio in un dato punto t₀. E per fare questo, terremo conto delle equazioni parametriche di una retta nello spazio.

Equazioni parametriche della retta tangente in un punto ad una curva parametrica dello spazio

Consideriamo una curva parametrica {\mathcal{C}} dello spazio, parametrizzata dalla funzione vettoriale {\textbf{f}:D \subseteq \R \rightarrow \R^3}:

\textbf{f}(t)=f_x(t)\textbf{i}+f_y(t)\textbf{j}+f_z(t)\textbf{k}

Supponiamo che in un certo punto {t_0 \in D} la funzione vettoriale {\textbf{f}(t)} sia derivabile. Dunque, ipotizziamo che esista la derivata di {\textbf{f}}(t) nel punto {t_0}, ovvero {\dfrac{d}{dt}\textbf{f}(t_0)}.

Ora, consideriamo la retta {r} passante per i punti della curva corrispondenti ai valori del parametro {t_0} e {t_0+\Delta t}, ovvero i punti individuati dai vettori posizione {\textbf{f}(t_0)} e {\textbf{f}(t_0+\Delta t)} (nelle figure indichiamo per comodità tali punti con i corrispondenti vettori posizione):

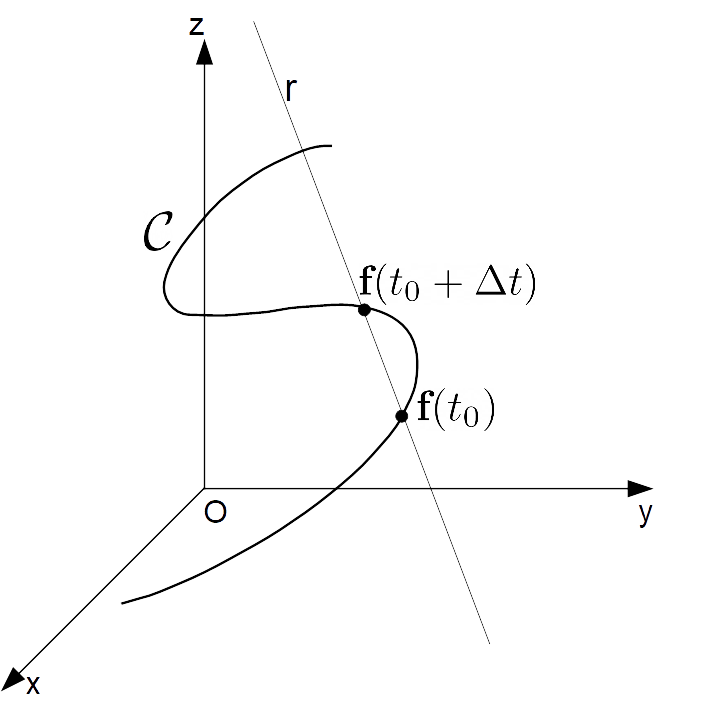
Tale retta è la retta secante della curva nei punti corrispondenti a {\textbf{f}(t_0}) e {\textbf{f}(t_0+\Delta t)}.

Ora, se rendiamo sufficientemente piccolo {\Delta t}, la retta {r} potrà essere utilizzata per approssimare la tangente alla curva {\mathcal{C}} nel punto {t_0}.

Effettivamente per {\Delta t} infinitamente piccolo la retta {r} coincide con la retta tangente alla curva {\mathcal{C}} nel punto corrispondente a {\textbf{f}(t_0)}:

Ora, il vettore {\textbf{f}}(t_0+\Delta t)-\textbf{f}(t_0) ha la stessa direzione della retta {r}.

Però, attenzione. Desideriamo che {\Delta t} diventi vicinissimo a zero, ma non uguale a zero. Diversamente il vettore {\textbf{f}}(t_0+\Delta t)-\textbf{f}(t_0) corrisponderebbe al vettore nullo ed avrebbe direzione indeterminata.

Tuttavia, per {\Delta t} infinitamente piccolo ma non nullo, il vettore:

\dfrac{1}{\Delta t} \cdot \Big(\textbf{f}(t_0+\Delta t)-\textbf{f}(t_0) \Big)

ha la stessa direzione della retta tangente alla curva nel punto corrispondente ad {\textbf{f}(t_0)} ed inoltre ha generalmente limite non nullo per {\Delta t \to 0}.

Di conseguenza, se facciamo tendere {\Delta t} a zero, ci aspettiamo che il vettore appena scritto abbia la stessa direzione della tangente alla curva {\mathcal{C}} nel punto corrispondente a {\textbf{f}(t_0)}. Se dunque vogliamo parametrizzare la retta tangente alla curva nel punto corrispondente a {\textbf{f}(t_0)} (ovvero scriverne le equazioni parametriche), è ragionevole pensare di utilizzare tale vettore come vettore parallelo a detta retta tangente, a patto di far tendere {\Delta t} a zero.

Possiamo formalizzare i ragionamenti sin qui fatti con la seguente definizione, nella quale interviene il concetto di derivata di una funzione vettoriale.

Equazioni parametriche della retta tangente ad una curva in un punto. Sia {P_0} un punto della curva {\mathcal{C}} dello spazio. Supponiamo che {\textbf{f}(t)} rappresenti una parametrizzazione della curva {\mathcal{C}}. Così {\overrightarrow{OP_0}=\textbf{f}(t_0)}.

Se {\dfrac{d}{dt}\textbf{f}(t_0)=\textbf{f}'(t_0)} esiste ed è diversa dal vettore nullo, allora la retta tangente alla curva {\mathcal{C}} nel punto {P_0} è data dalla retta che passa per il punto {P_0} e parallela a {\textbf{f}'(t_0)}.

Tale retta tangente è in particolare parametrizzabile come: {\textbf{g}(u)=\textbf{f}(t_0)+u \textbf{f}'(t_0)}

Osserviamo che la parametrizzazione appena scritta per la retta tangente alla curva {\mathcal{C}} nel punto {P_0} può essere anche espressa con le seguenti equazioni parametriche scalari:

\begin{cases} x = x_0 + u \cdot  \dfrac{d}{dt}f_x(t_0) \\ \\ y = y_0 + u \cdot \dfrac{d}{dt}f_y(t_0) \\ \\  z = z_0 + u  \cdot\dfrac{d}{dt}f_z(t_0)\end{cases}

Così, un vettore {\textbf{m}} parallelo alla retta tangente alla curva nel punto {P_0} è dato da:

\textbf{m}=\dfrac{d}{dt}\textbf{f}(t_0)=\textbf{f}'(t_0)=\left \langle {\dfrac{d}{dt}f_x(t_0), \:\dfrac{d}{dt}f_y(t_0), \: \dfrac{d}{dt}f_z(t_0)} \right \rangle

Ciò mette in evidenza il fatto che, per la definizione data, la derivata della funzione vettoriale {\textbf{f}(t)} in corrispondenza di {t=t_0} ha la stessa direzione della retta tangente alla curva {\mathcal{C}} nel punto {P_0}.

Per convincersi di questo, basta ricordare la definizione di derivata di una funzione vettoriale in un punto {t_0}:

\dfrac{d}{dt}\textbf{f}(t_0)=\lim_{\Delta t \to 0}\dfrac{1}{\Delta t} \cdot \Big(\textbf{f}(t_0+\Delta t)-\textbf{f}(t_0) \Big)

Effettivamente è proprio grazie alla definizione di derivata che riusciamo, tramite il processo di limite, a far tendere {\Delta t} a zero, di modo che il vettore {\textbf{f}(t_0 + \Delta t)-\textbf{f}(t_0)} abbia al limite la stessa direzione della retta tangente alla curva {C} nel punto {P_0}. Ora, anche il secondo membro dell’equazione appena scritta ha la stessa direzione di tale retta tangente. Quindi, la direzione del vettore {\dfrac{d}{dt}\textbf{f}(t_0)} è la stessa della retta tangente considerata. Così, in conclusione, le equazioni parametriche scritte sono corrette.

Esempio (come determinare le equazioni parametriche della retta tangente in un punto ad una curva nello spazio)

Data la curva parametrizzata dalla funzione vettoriale:

\textbf{f}(t)=t \cdot\cos(t) \textbf{i}+ t \cdot \sin(t)\textbf{j}+t\textbf{k}

scrivere le equazioni parametriche della retta tangente alla curva nel punto {P_0=(0, \pi/2, \pi/2}).

Ricordiamo che le equazioni parametriche di una retta nello spazio sono della forma (utilizziamo un parametro {u}):

\begin{cases} x=x_0+u \cdot a \\ \\ y=y_0+u \cdot b \\ \\ z=z_0 +u\cdot c\end{cases}

ove {a, \: b, \: c} sono le componenti cartesiane di un vettore {\textbf{m}} parallelo alla retta da parametrizzare e {x_0, \: y_0, \: z_0} sono le coordinate di un punto appartenente alla retta noto.

Per scrivere le equazioni parametriche di una retta nello spazio abbiamo quindi bisogno di un vettore parallelo alla retta e delle coordinate di un punto appartenente alla retta. Nel nostro caso, queste ultime sono note e sono le coordinate del punto {P_0=(0, \pi/2, \pi/2)}.

Poi, sappiamo che la derivata della funzione vettoriale che rappresenta la curva, valutata nel punto {P_0}, è un vettore parallelo alla retta tangente alla curva stessa nel punto {P_0}. Cominciamo allora calcolando (vedi: derivata di una funzione vettoriale):

\begin{align*} & \dfrac{d}{dt}\textbf{f}(t)=\dfrac{d}{dt}\Big(t \cdot\cos(t) \textbf{i}+ t \cdot \sin (t)\textbf{j}+t\textbf{k} \Big)=\\ \\ & =[\cos(t)-t\sin(t)]\textbf{i}+[\sin(t)+t\cos(t)]\textbf{j}+\textbf{k} \end{align*}

Ma a questo punto occorre determinare il vettore:

\textbf{m}=\dfrac{d}{dt}\textbf{f}(t)\Big|_{t=t_0}=\textbf{f}'(t_0)

ma non conosciamo per il momento il valore {t_0}.

Ora, per individuare il valore {t_0} basta osservare che le coordinate del punto {P_0} sono uguali alle componenti cartesiane del vettore {\textbf{f}(t_0)}. Ciò si giustifica per la definizione di vettore posizione, ed effettivamente {\textbf{f}(t_0)=\overrightarrow{OP_0}} è il vettore posizione di {P_0}.

Abbiamo quindi:

\begin{cases} x_0=f_x(t_0) \\ \\ y_0=f_y(t_0) \\ \\ z_0=f_z(t_0)  \end{cases} \iff \begin{cases} 0 = t _0 \cos (t_0) \\ \\ \dfrac{\pi}{2}=t_0\sin(t_0) \\ \\ \dfrac{\pi}{2}=t_0\end{cases}

da cui segue immediatamente (ultima equazione del sistema):

 t_0=\dfrac{\pi}{2}

Ora possiamo finalmente scrivere un vettore parallelo alla retta da parametrizzare valutando {f}'(t) in {t_0}:

\small \begin{align*} &\dfrac{d}{dt}\textbf{f}(t)\Big|_{t=t_0}=[\cos(t_0)-t_0\sin(t_0)]\textbf{i}+[\sin(t_0)+t_0\cos(t_0)]\textbf{j}+\textbf{k}=\\ \\ & =\left[\cos\left( \dfrac{\pi}{2}\right)-\dfrac{\pi}{2}\sin\left( \dfrac{\pi}{2}\right)\right]\textbf{i}+\left[ \sin \left( \dfrac{\pi}{2}\right)+\dfrac{\pi}{2}\cos \left( \dfrac{\pi}{2}\right)\right]\textbf{j}+\textbf{k}=\\ \\ & =-\dfrac{\pi}2{\textbf{i}+\textbf{j}+\textbf{k}}=\left \langle {-\dfrac{\pi}2{,1,1}} \right \rangle = \left \langle {a, b, c} \right \rangle=\textbf{m}\end{align*}

Così possiamo scrivere in conclusione le equazioni parametriche della retta tangente alla curva data nel punto {P_0=(0, \pi/2, \pi/2)} come:

\begin{cases} x=x_0+ u \cdot a \\ \\ y=y_0+u \cdot b \\ \\ z=z_0+u \cdot c\end{cases} \quad \Rightarrow \quad \begin{cases} x=0-\dfrac{\pi}{2}u \\ \\ y=\dfrac{\pi}{2}+u \\ \\ z=\dfrac{\pi}{2}+u\end{cases}

Osserviamo che nello scrivere la parametrizzazione della retta tangente alla curva in {P_0} occorre utilizzare un nuovo parametro {u}, diverso dal parametro {t} utilizzato per parametrizzare la curva.

Concludiamo l’esercizio rappresentando graficamente la curva {\mathcal{C}} e la retta ad essa tangente nel punto {P_0}:

Direzione del vettore velocità

Se una curva {\mathcal{C}} dello spazio rappresenta la traiettoria di un corpo puntiforme (particella), e se {f}(t) è la funzione vettoriale che parametrizza la stessa curva {\mathcal{C}}, la velocità del corpo puntiforme all’istante {t} è data da:

\dfrac{d}{dt}\textbf{f}(t)

E considerando un dato istante {t_0}, la velocità della particella per {t=t_0} si ottiene valutando la precedente derivata proprio in {t_0}:

\dfrac{d}{dt}\textbf{f}(t)\Big|_{t=t_0}

Ora, per quanto visto in questa lezione, possiamo affermare che la velocità istantanea della particella nell’istante {t=t_0} è un vettore la cui direzione è uguale a quella della retta tangente alla curva nel punto {P_0} corrispondente a {\textbf{f}(t_0)}.

Esempio (direzione della velocità istantanea di una particella)

Determinare la velocità nell’istante {t=2} di una particella che descrive una traiettoria corrispondente alla funzione vettoriale:

\textbf{f}(t)=2t^2\textbf{i}+5 t\textbf{\textbf{j}}+3t^3\textbf{k}

Scrivere inoltre le equazioni parametriche della retta avente la stessa direzione del vettore velocità.

Osserviamo che nell’istante {t=2} la funzione {\textbf{f}(t)} ha per valore il vettore:

\textbf{f}(2)=2\cdot2^2\textbf{i}+5\cdot2\textbf{j}+3\cdot2^3\textbf{k}=8\textbf{i}+10\textbf{j}+24\textbf{k}

Di conseguenza per {t=2} la particella si trova nel punto {P_0=(8, 10, 24)}.

Calcoliamo il vettore velocità (velocità istantanea):

\begin{align*} & \dfrac{d}{dt}\textbf{f}(t)=\left( \dfrac{d}{dt}2t^2\right)\textbf{i}+\left( \dfrac{d}{dt}5t\right)\textbf{j}+\left( \dfrac{d}{dt}3t^3\right)\textbf{k}=\\ \\ & =4t\textbf{i}+5\textbf{j}+9t^2\textbf{k} \end{align*}

La velocità della particella all’istante {t=2} è data da:

\dfrac{d}{dt}\textbf{f}(t) \Big|_{t=2}=4 \cdot 2 \textbf{i}+5\textbf{j}+9\cdot2^2\textbf{k}=8\textbf{i}+5\textbf{j}+36\textbf{k}

Il vettore ottenuto è un vettore parallelo alla retta tangente alla traiettoria descritta dalla particella nel punto {P_0=(8, 10, 24)}. Di conseguenza, tale retta tangente avrà equazioni parametriche:

\begin{cases} x = 8+8u \\ \\ y=10+5u \\ \\ z=24+36u\end{cases}

Graficamente otteniamo la seguente rappresentazione:

Per quanto riguarda la retta tangente in un punto ad una curva dello spazio è tutto. Nella prossima lezione faremo la conoscenza del vettore accelerazione (accelerazione istantanea). Buon proseguimento!