Equazioni parametriche di una retta nello spazio

Le equazioni parametriche di una retta nello spazio sono delle equazioni scalari che permettono di descrivere una retta nello spazio mediante un parametro reale t. In altre parole, le coordinate cartesiane del generico punto P del piano vengono tutte espresse in funzione del parametro t. Le equazioni parametriche di una retta si ricavano a partire da un punto P₀appartenente alla retta e da un vettore m avente direzione parallela alla retta stessa.

Equazione parametrica vettoriale ed equazioni parametriche scalari di una retta nello spazio

Consideriamo una retta ${r}$ , un punto ${P_0}$ appartenente ad ${r}$ ed un vettore ${\textbf{m}=\left \langle {a,b,c} \right \rangle}$ parallelo alla retta stessa.

Ora, un generico punto ${P=(x,y,z)}$ apparterrà alla retta ${r}$ se e solo se il vettore ${\overrightarrow{P_0P}}$ è parallelo al vettore ${\textbf{m}}$ . Di conseguenza, dovrà essere possibile esprimere il vettore ${\overrightarrow{P_0P}}$ come multiplo scalare di ${\textbf{m}}$ , ovvero dovremo avere ${\overrightarrow{P_0P}=t \textbf{m}}$ per un certo scalare ${t}$ .

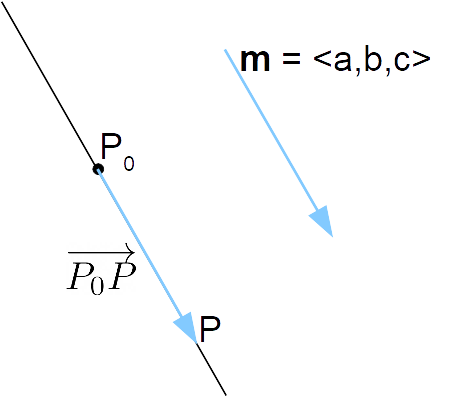
Così, ogni punto ${P=(x,y,z)}$ appartenente alla retta ${r}$ dovrà soddisfare l’equazione vettoriale:

\overrightarrow{P_0P}=t \cdot \textbf{m}, \qquad t \in \R

che è l’equazione parametrica vettoriale della retta r nello spazio, ove ${t}$ è un parametro reale.

Come abbiamo visto nella precedente lezione sulle equazioni parametriche di un piano nello spazio, da un’equazione vettoriale è possibile passare alle corrispondenti equazioni scalari. Nel nostro caso, tenendo conto che ${\overrightarrow{P_0P}=\left \langle {x-x_0, y-y_0, z-z_0} \right \rangle}$ , abbiamo le equazioni scalari:

\begin{cases} x-x_0=t\cdot a \\ \\ y-y_0=t \cdot b \\ \\ z-z_0=t \cdot c \\ \\ \end{cases}

ovvero:

\begin{cases}x=x_0+t\cdot a \\ \\ y=y_0+t \cdot b \\ \\ z=z_0 + t \cdot c \end{cases}

e queste sono le equazioni parametriche scalari di una retta r nello spazio tridimensionale.

Riassumiamo tutto quanto sin qui detto come segue.

La retta nello spazio che è parallela al vettore ${\textbf{m}=\left \langle {a,b,c} \right \rangle}$ e passa per il punto ${P_0=(x_0, y_0, z_0)}$ ha la seguente equazione parametrica vettoriale: ${\overrightarrow{P_0P}=t \cdot \textbf{m}}$ alla quale corrispondono le seguenti equazioni parametriche scalari della retta ${r}$ ${\begin{cases} x=x_0+t\cdot a \\ \\ y=y_0+t \cdot b \\ \\ z=z_0 + t \cdot c \end{cases}}$ ove ${t}$ è un parametro reale.

NOTA: l’equazione parametrica vettoriale di una retta nello spazio si può anche scrivere nella forma:

\textbf{r}(t)=\textbf{r}(t_0)+t \cdot \textbf{m}

ove ${\textbf{r}(t)}$ e ${\textbf{r}(t_0)}$ sono i vettori posizione corrispondenti al generico valore ${t}$ del parametro e ad un certo valore ${t_0}$ del parametro stesso. Questa definizione alternativa sarà più chiara quando studieremo le funzioni vettoriali.

Vediamo ora degli esempi su come mettere in pratica le nozioni sin qui acquisite.

Esempi sulle equazioni parametriche di una retta dello spazio

Esempio 1

Scrivere un punto che appartiene alla retta ${r}$ di equazioni parametriche (scalari): ${\begin{cases}x=3t+1 \\ \\ y=5t \\ \\ z=t-2 \end{cases}}$

Osserviamo che le equazioni parametriche di una retta ${r}$ individuano un punto ${P}$ di ${r}$ per ogni fissato valore del parametro ${t}$ . Così, per scrivere le coordinate di un punto appartenente alla retta ${r}$ , basterà fissare a piacere un valore del parametro reale ${t}$ e ricavare le corrispondenti coordinate del punto ${P}$ . Ad esempio, ponendo ${t=1}$ abbiamo:

\begin{cases}x=3 \cdot 1+1 \quad \rightarrow \quad x = 4 \\ \\ y=5 \cdot 1 \quad \rightarrow \quad y = 5 \\ \\ z=1-2 \quad \rightarrow \quad z=-1 \end{cases}

Così possiamo in conclusione affermare che un punto appartenente alla retta ${r}$ è ${P=(4,5,-1)}$ .

Esempio 2

Determinare se i punti ${P_1=(2,3,7)}$ e ${P_2=(3,1,1)}$ appartengono alla retta ${r}$ di equazioni: ${\begin{cases} x=t+1 \\ \\ y=2t-3 \\ \\ z=3t-5\end{cases}}$ con ${t}$ parametro reale.

L’idea è quella di sostituire in ciascuna equazione parametrica della retta ${r}$ le coordinate di ciascun punto da testare, per poi ricavare il valore del parametro ${t}$ . Se per ciascuna equazione otteniamo uno stesso valore del parametro, allora il punto in esame appartiene alla retta ${r}$ .

Consideriamo il primo punto, ovvero ${P_1=(2,3,7)}$ . Sostituiamo le sue coordinate ${x, \: y, \: z}$ in ciascuna equazione parametrica:

\begin{cases} 2=t+1 \quad \rightarrow \quad t=1 \\ \\ 3=2t-3 \quad \rightarrow \quad t=3 \\ \\ 7=3t-5 \quad \rightarrow \quad t=4\end{cases}

Poiché non otteniamo per ogni equazione uno stesso valore del parametro, il punto ${P_1=(2,3,7)}$ non appartiene alla retta ${r}$ .

Vediamo se abbiamo più fortuna con il punto ${P_2=(3,1,1)}$ :

\begin{cases} 3=t+1 \quad \rightarrow \quad t=2 \\ \\ 1=2t-3 \quad \rightarrow \quad t=2 \\ \\ 1=3t-5 \quad \rightarrow \quad t=2\end{cases}

Stavolta otteniamo da ciascuna equazione uno stesso valore del parametro, per cui il punto ${P_2=(3,1,1)}$ appartiene alla retta ${r}$ .

Esempio 3

Data la retta ${r}$ di equazioni parametriche (scalari): ${\begin{cases} x=-5+3t \\ \\ y=7-8t \\ \\ z=1+2t\end{cases}}$ scrivere le equazioni della retta parallela ad ${r}$ e passante per l’origine.

Consideriamo le equazioni di una retta ${r}$ nella forma:

\begin{cases} x-x_0=t\cdot a \\ \\ y-y_0=t \cdot b \\ \\ z-z_0=t \cdot c \end{cases}

Nel nostro caso, riscrivendo le equazioni parametriche date proprio in questa forma, otteniamo:

\begin{cases} x+5=3t \\ \\ y-7=-8t \\ \\ z-1=2t\end{cases}

Deduciamo quindi effettuando un immediato confronto che ultime equazioni scritte sono relative ad una retta passante per il punto ${P_0=(5,-7,-1)}$ . Di conseguenza, le equazioni parametriche della retta parallela a quella data ma passante per il punto ${O=(x_0, y_0, z_0)=(0,0,0)}$ sono:

\begin{cases} x=3t \\ \\ y=-8t \\ \\ z=2t\end{cases}

Osserviamo che le equazioni parametriche appena scritte sono relative ad una retta ${r'}$ parallela alla retta ${r}$ di partenza, in quanto in esse figurano al secondo membro le quantità rispettivamente ${3t, \: -8t, \: 2t }$ . Queste sono infatti le componenti cartesiane del vettore ${t\textbf{m}=\left \langle {3, -8, 2} \right \rangle t}$ , che è anche parallelo alla retta di partenza.

Conclusioni

Per quanto riguarda questa lezione è tutto. Nella prossima lezione ci occuperemo delle equazioni cartesiane di una retta nello spazio, e vedremo come poter passare dall’equazione cartesiana alle equazioni parametriche, e viceversa. Buon proseguimento!