Alcune proprietà delle operazioni tra insiemi sono ovvie, altre invece possono essere dimostrate. La maggior parte delle proprietà non saranno dimostrate. Troverete invece la dimostrazione delle Leggi di De Morgan. Una tale dimostrazione è a mio parere un’ottima palestra per lavorare con le proprietà delle operazioni tra insiemi.
Proprietà delle operazioni tra insiemi
Elenchiamo a seguire le proprietà delle operazioni tra insiemi, raggruppate per ogni singola operazione.
Proprietà dell’operazione di unione di insiemi
L’unione di un insieme con sé stesso ha come risultato tale insieme. In simboli:
\[ A \cup A = A \]
L’unione di un insieme con l’insieme vuoto ha come risultato l‘insieme stesso. In simboli:
\[ A \cup \emptyset = A \]
Ciò è ovvio ricordando che l’insieme vuoto è un insieme privo di elementi.
L’operazione di unione gode inoltre delle seguenti proprietà.
Proprietà commutativa:
\[ A \cup B = B \cup A \]
Proprietà associativa:
\[ A \cup (B \cup C) = (A \cup B) \cup C \]
Proprietà dell’operazione di intersezione tra insiemi
L’intersezione di un insieme con sé stesso ha come risultato l’insieme di partenza. In simboli:
\[ A \cap A = A \]
Ciò è evidente poiché un qualunque insieme ha tutti gli elementi in comune con sé stesso.
L’intersezione di un insieme con l’insieme vuoto ha come risultato l’insieme vuoto. In simboli:
\[ A \cap \emptyset = \emptyset \]
L’operazione di intersezione gode delle seguenti ulteriori proprietà.
Proprietà commutativa:
\[ A \cap B = B \cap A \]
Proprietà associativa:
\[ A \cap (B \cap C) = (A \cap B) \cap C \]
Proprietà distributiva
Le operazioni di unione e intersezione di insiemi non godono singolarmente della proprietà distributiva. Possiamo però definire le seguenti proprietà.
Proprietà distributiva dell’unione rispetto all’intersezione:
\[ A \cup (B \cap C)=(A \cup B) \cap (A \cup C) \]
Proprietà distributiva dell’intersezione rispetto all’unione:
\[ A \cap (B \cup C) = (A \cap B) \cup (A \cap C) \]
Proprietà dell’operazione differenza tra insiemi
Abbiamo le seguenti proprietà:
\[ A \setminus A = \emptyset \]
\[ A \setminus \emptyset = A \]
Le proprietà discendono direttamente dalla definizione di insieme differenza.
Proprietà dell’operazione di determinazione dell’insieme complementare
Il complementare del complementare di un insieme (rispetto ad un fissato universo) e’ pari proprio all’insieme
Fissato un qualsiasi insieme universo \( U \), sussiste la proprietà:
\[ \mathcal{C}_U(\mathcal{C}_UA)=A \]
Cioè, il complementare del complementare di un insieme \( A \) rispetto ad un universo \( U \) è proprio l’insieme \( A \).
Tale proprietà ha la sua analoga in logica (per chi già conosce la logica): negando due volte una proposizione, si ottiene la proposizione di partenza.
L’intersezione di un insieme con il suo complementare (RISPETTO AD un fissato universo) E’ pari all’insieme vuoto
In simboli:
\[ A \cap \mathcal{C}_UA=\emptyset \]
Ciò è di immediata comprensione, considerando che l’insieme complementare di un insieme non ha per definizione elementi in comune con l’insieme stesso. Per cui non esistono elementi che appartengono sia ad un insieme, sia al complementare di quello stesso insieme.
Di conseguenza:
\[ x \in A \iff x \notin \mathcal{C}_UA \]
e:
\[ x \in \mathcal{C}_U A \iff x \notin A \]
L’Unione di un insieme con il suo complementare rispetto ad un fissato universo e’ pari all’universo stesso
In simboli:
\[ A \cup \mathcal{C}_UA=U \]
Il concetto è intuitivo ma possiamo giustificarlo osservando che poiché \( \mathcal{C}_UA=U \setminus A \) , si ha che \( (U \setminus A) \cup A = U \). Togliendo ad \( U \) gli elementi di \( A \) e poi aggiungendo di nuovo ad \( U \) tali elementi, otteniamo di nuovo \( U \). Ciò è corretto poiché \( A \subseteq U \), cioè \( A \) sarà sempre un sottoinsieme proprio di \( U \) o al massimo potrà coincidere con \( U \).
NOTA: osserviamo infatti che, in generale, dati due insiemi \( A \) e \( B \):
\[ (A \setminus B ) \cup B \neq A \]
Abbiamo l’uguaglianza soltanto se \( B \subseteq A \).
Ulteriori proprieta’ che nascono dalla definizione di insieme complementare
Il complementare rispetto all’insieme universo dell’insieme universo stesso è pari all’insieme vuoto:
\[ \mathcal{C}_U U=\emptyset \]
Inoltre, il complementare dell’insieme vuoto è pari all’insieme universo:
\[ \mathcal{C}_U\emptyset = U \]
Entrambe le proprietà sono intuitive ricordando che il complementare di un insieme rispetto ad un dato universo può essere riletto con l’operazione di differenza: \( \mathcal{C}_U A = U \setminus A \). Per cui è sufficiente porre nella relazione appena scritta rispettivamente \( A = U \) e \( A = \emptyset \) 😉
In particolare effettuando tali sostituzioni abbiamo che \( U \setminus U = \emptyset \) (l’insieme degli elementi che appartengono ad \( U \)e che allo stesso tempo NON appartengono ad \( U \) è chiaramente vuoto) e \( U \setminus \emptyset = U \) (cioè è ovvio poiché l’insieme vuoto non ha alcun elemento).
Leggi di De Morgan
Le leggi di De Morgan sono formule che mettono in relazione l’insieme complementare con le operazioni di unione ed intersezione.
Prima legge di de morgan
Il complementare dell’unione dei due insiemi \( A \) e \( B \) è uguale all’intersezione del complementare di \( A \) con il complementare di \( B \). In simboli:
\[ \mathcal{C}_U (A \cup B) = \mathcal{C}_U A \cap \mathcal{C}_U B \]
Seconda legge di de morgan
Il complementare dell’insieme intersezione degli insiemi \( A \) e \( B \) è pari all’unione del complementare di \( A \) con il complementare di \( B \). In simboli:
\[ \mathcal{C}_U (A \cap B) = \mathcal{C}_U A \cup \mathcal{C}_U B \]
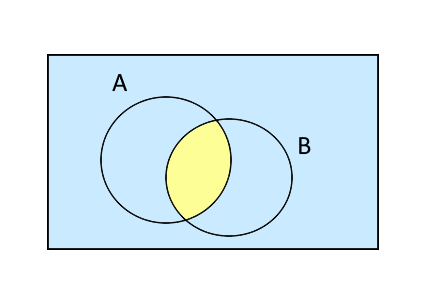
Nelle leggi di De Morgan compaiono tre insiemi: l’insieme universo \( U \) e due insiemi \( A \) e \( B \). Dunque, poiché l’universo scelto è \( U \), si ha in generale \( A \subseteq U \) e \( B \subseteq U \). Le leggi si rivelano utili però considerando \( A \subset U \), \( B \subset U \), cioè prendendo due sottoinsiemi propri dell’universo fissato.
Dimostrazione delle leggi di De Morgan
E’ possibile dimostrare le leggi di De Morgan utilizzando le proprietà delle operazioni tra insiemi sin qui presentate. Con ciò, cerchiamo di andare oltre rispetto ad una verifica grafica che per quanto interessante non può avere il valore di una dimostrazione.
Una doverosa premessa: tale dimostrazione non sarà mai richiesta a scuola e raramente all’università. Tuttavia, essa rappresenta a mio parere un utile esercizio.
Possiamo leggere ciascuna legge di De Morgan come un’uguaglianza tra due insiemi \( D \) ed \( E \) (i quali rappresentano, rispettivamente, ciò che sta a sinistra e a destra dell’uguale in ciascuna legge). Dimostrare le leggi di De Morgan equivarrà a dimostrare che \( D = E \) per ciascuna di essa.
Come sappiamo, dimostrare che \( D = E \) equivale a dimostrare che \( D \subseteq E \) e che contemporaneamente \( E \subseteq D \).
In altre parole, per iniziare dobbiamo dimostrare che se un elemento \( k \in D \), allora l’elemento appartiene necessariamente anche all’insieme \( E \). E con ciò viene dimostrato che \( D \subseteq E \). Poi, dovremo dimostrare che se un elemento \( j \) appartiene all’insieme \( E \), allora questo elemento appartiene necessariamente anche all’insieme \( D \). In tal modo, si dimostra anche l’inclusione \( E \subseteq D \). Mettendo insieme le due relazioni di inclusione ottenute, si dimostra l’uguaglianza tra i due insiemi \( D \) ed \( E \).
Seguendo tale traccia possiamo dimostrare entrambe le leggi di De Morgan. Sottintenderemo per comodità che l’insieme universo fissato sia \( U \).
Dimostrazione della prima legge di de morgan
L’enunciato della prima legge di De Morgan è:
\[ \mathcal{C}(A \cup B)= \mathcal{C}A \cap \mathcal{C}B \]
Poniamo \( D = \mathcal{C}(A \cup B) \) e \( E =\mathcal{C}A \cap \mathcal{C}B \).
Consideriamo un elemento \( k \in D \). Poiché se un elemento appartiene al complementare di un insieme, allora esso non può appartenere all’insieme, si ha:
\[ k \notin (A \cup B) \]
Sfruttando la definizione di insieme unione, ciò significa che:
\[ k \notin A \quad \text{et} \quad k \notin B \]
cioè se un elemento non deve appartenere all’unione dei due insiemi, allora esso non dovrà appartenere a nessuno dei due insiemi. Ovvero, non dovrà appartenere contemporaneamente né ad \( A \), né a \( B \).
Ma se un elemento non appartiene ad un insieme, esso apparterrà per forza al complementare dell’insieme. La precedente si può riscrivere quindi come:
\[ k \in \mathcal{C}A \quad \text{et} \quad k \in \mathcal{C}B \]
Sfruttando la definizione di insieme intersezione, si ha di conseguenza:
\[ k \in (\mathcal{C}A \cap \mathcal{C}B) \]
E abbiamo ritrovato l’insieme \( E \). Quindi ipotizzando che \( k \in D \), otteniamo che \( k \in E \). Di conseguenza possiamo dire che \( D \subseteq E \).
Ci rimane ora da dimostrare che \( E \subseteq D \).
Ipotizziamo che \( j \in E \). Sfruttando la definizione di insieme intersezione, si ha equivalentemente:
\[ j \in \mathcal{C}A \quad \text{et} \quad j \in \mathcal{C}B \]
e, poiché se un elemento appartiene al complementare di un insieme allora non appartiene all’insieme, si ha:
\[ j \notin A \quad \text{et} \quad j \notin B \]
e, per come è definita l’operazione di unione:
\[ j \notin (A \cup B) \]
Infatti, se un elemento non deve appartenere ad entrambi gli insiemi, allora non deve appartenere nemmeno all’unione dei due insiemi.
Ma allora l’elemento appartiene al complementare dell’unione degli insiemi:
\[ j \in \mathcal{C}(A \cup B) \]
Abbiamo così ritrovato l’insieme \( D \). Si ha quindi che ipotizzando che un elemento appartiene all’insieme \( E \), allora questo apparterrà necessariamente all’insieme \( D \). Di conseguenza \( E \subseteq D \).
Abbiamo quindi dimostrato che:
\[ D \subseteq E \quad \text{et} \quad E \subseteq D \]
cioè che:
\[ D = E \]
Per come abbiamo assegnato gli insiemi \( D \) ed \( E \), ciò equivale ad aver dimostrato la prima legge di De Morgan.
Dimostrazione della seconda legge di de morgan
L’enunciato della seconda legge di De Morgan è:
\[ \mathcal{C_U} (A \cap B) = \mathcal{C_U}A \cup \mathcal{C_U}B \]
Poniamo stavolta \( D=\mathcal{C_U} (A \cap B) \) e \( E=\mathcal{C_U}A \cup \mathcal{C_U}B \).
Ipotizziamo che l’elemento \( k \) appartiene a \( D \).
Si ha allora:
\[ k \notin (A \cap B) \]
Quindi, per come è definita l’operazione di intersezione tra insiemi:
\[ k \notin A \quad \text{oppure} \quad k \notin B \]
E’ immediato convincersi di questa scrittura equivalente considerando che nell’insieme intersezione nessuna delle due condizioni è verificata. Dunque la precedente equivale effettivamente a dire che \( k \notin (A \cap B) \).
Di conseguenza:
\[ k \in \mathcal{C}A \quad \text{oppure} \quad k \in \mathcal{C}B \]
ma allora:
\[ k \in (\mathcal{C}A \cup \mathcal{C}B) \quad \Rightarrow \quad k \in E \]
Quindi abbiamo dimostrato che:
\[ D \subseteq E \]
Rimane ora da dimostrare che \( E \subseteq D \).
Ipotizziamo che un elemento \( j \in E \). Per come è definita l’operazione di unione tra insiemi, si ha:
\[ j \in \mathcal{C} A \quad \text{oppure} \quad j \in \mathcal{C} B \]
di conseguenza:
\[ j \notin A \quad \text{oppure} \quad j \notin B \]
In altre parole, richiediamo che sia vera almeno una delle due condizioni. Se siamo nell’insieme \( A \) o nell’insieme \( B \), evidentemente una delle due condizioni sarà comunque soddisfatta. Infatti, se siamo in \( A \), comunque l’elemento non appartiene a \( B \). Se siamo in \( B \), comunque l’elemento non appartiene ad \( A \). Il problema è quando un elemento appartiene contemporaneamente ad \( A \) e a \( B \). In tale circostanza è facile convincersi che nessuna delle due condizioni è verificata. Pertanto, l’elemento non potrà appartenere contemporaneamente agli insiemi \( A \) e \( B \). Di conseguenza, l’elemento non potrà appartenere all’insieme intersezione tra i due insiemi, proprio per come è definita l’operazione di intersezione. Si ha quindi:
\[ j \notin (A \cap B) \]
Però possiamo scrivere:
\[ j \in \mathcal{C}(A \cap B) \]
Abbiamo ritrovato così l’insieme \( D \). Si è dunque dimostrato che se ipotizziamo che un elemento appartiene all’insieme \( E \), allora questo appartiene necessariamente all’insieme \( D \). Si ha quindi:
\[ E\subseteq D \]
E poiché abbiamo già dimostrato che \( D \subseteq E \), si ha:
\[ D = E \]
Per come abbiamo assegnato gli insiemi \( D \) ed \( E \), anche la seconda legge di De Morgan è dimostrata.
Siamo dunque arrivati alla conclusione di questa lezione relativa alle proprietà delle operazioni tra insiemi.
Nella prossima lezione vedremo il concetto di partizione di un insieme. Ciao a tutti! 🙂
Riferimenti usati/si ringrazia: Proof of De Morgan’s Laws
