La partizione di un insieme è dunque un insieme costituito da insiemi, al pari dell’insieme potenza. Tuttavia, il concetto di partizione e quello di insieme potenza (detto anche insieme delle parti) sono due concetti completamente diversi. Quindi, per favore attenzione 😉 La partizione e l’insieme delle parti di un insieme, nonostante le somiglianze nel nome, sono costruiti ciascuno in modo totalmente differente.
Vedremo infine come il concetto di insieme complementare possa essere utile per costruire una partizione di un insieme.
Partizione di un insieme
Dato un insieme \( A \) non vuoto, una partizione dell’insieme \( A \) è data da un gruppo di sottoinsiemi propri di \( A \) tali che:
- ogni sottoinsieme è diverso dall’insieme vuoto, ovvero ogni sottoinsieme ha almeno un elemento;
- i sottoinsiemi sono a due a due disgiunti, ovvero presa una qualunque coppia di sottoinsiemi, i due sottoinsiemi non hanno tra loro elementi in comune;
- l’unione di tutti questi sottoinsiemi è pari all’insieme \( A \).
La proprietà 2 può essere espressa in modo equivalente dicendo che, presa una qualunque coppia di sottoinsiemi di \( A \), i due sottoinsiemi della coppia per far parte della partizione devono avere come loro intersezione l’insieme vuoto.
Uscendo per un attimo dal linguaggio matematico, possiamo immaginare l’insieme \( A \) come la superficie calpestabile della nostra camera. Ciascuna mattonella è un sottoinsieme proprio dell’insieme \( A \). L’unione di tutte le mattonelle forma il pavimento della nostra camera. Il gruppo di tutte le mattonelle della nostra camera costituisce una partizione poiché ciascuna mattonella individua una sua propria superficie (non si sovrappone a nessun’altra mattonella), la superficie individuata da ciascuna mattonella è non nulla e la loro unione ha come risultato l’insieme \( A \) (appunto, il pavimento della camera).
Graficamente, possiamo vedere una partizione di un insieme come segue:
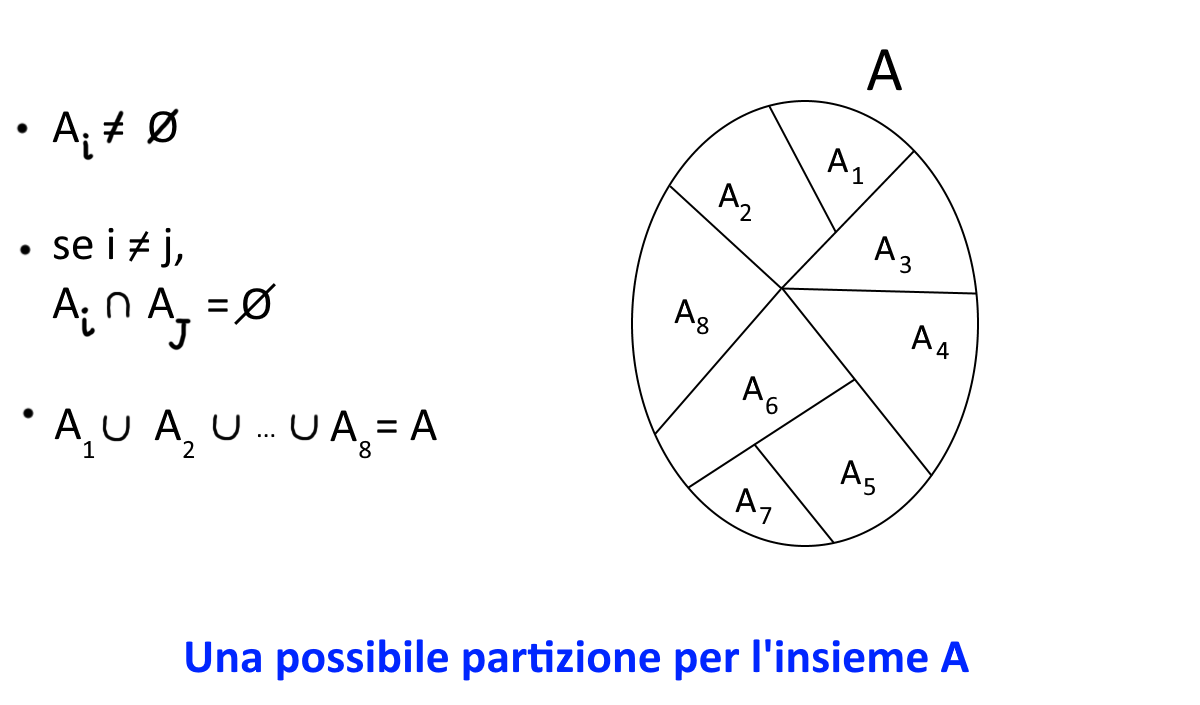
Nella figura, \( i \) e \( j \) sono due numeri naturali che rappresentano gli indici dei sottoinsiemi propri di \( A \). Si può stabilire infatti di rappresentare i sottoinsiemi della partizione con la stessa lettera dell’insieme di partenza accompagnata da un indice in pedice. Ciò è comodo quando abbiamo molti sottoinsiemi in una partizione. In ogni caso, l’uso degli indici ben si presta a rappresentare in modo simbolico le condizioni di appartenenza di un sottoinsieme alla partizione, come mostra la figura.
Requisiti per l’insieme del quale si vuole scrivere una partizione
Affinché sia possibile scrivere la partizione di un insieme, è necessario che l’insieme sia diverso dall’insieme vuoto. Dunque, non esiste alcuna partizione dell’insieme vuoto.
Qualora l’insieme sia costituito da un solo elemento, è possibile effettuarne la partizione. Tuttavia, l’unica partizione possibile sarà costituita, banalmente, dall’insieme stesso.
Dunque, si parlerà generalmente di partizione di un insieme con riferimento ad insiemi costituiti da più elementi.
E’ importante osservare che in generale una partizione può essere costruita in diversi modi, come vedremo in un esempio tra poco.
Insieme complementare e partizione di un insieme
Sia dato un insieme \( A \) non vuoto e sia fissato un universo \( U \). Sia \( A \subset U \), cioè l’insieme \( A \) sia un sottoinsieme proprio di \( U \). Sotto queste ipotesi, il complementare dell’insieme \( A \) rispetto all’universo \( U \) e lo stesso insieme \( A \) costituiscono una possibile partizione per l’insieme universo \( U \).
Infatti, l’insieme \( A \) e il suo complementare rispettano le proprietà che devono avere un gruppo di sottoinsiemi per individuare una partizione:
- \( A \neq \emptyset; \quad \mathcal{C}_U A \neq \emptyset \)
- \( A \cap \mathcal{C}_UA=\emptyset \);
- \( A \cup \mathcal{C}_UA=U \).
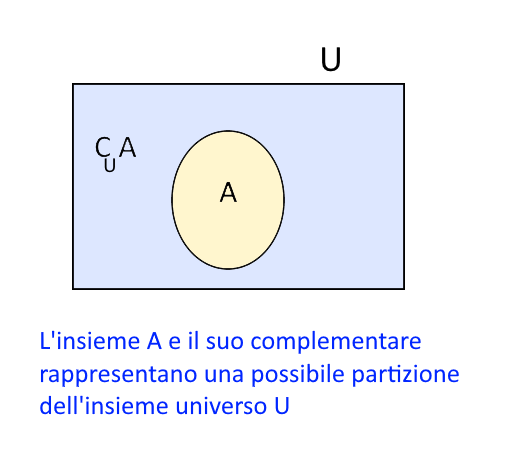
L’insieme \( A \) deve essere un sottoinsieme proprio di \( U \) per evitare che possa essere \( A=U \). In tal caso infatti il complementare di \( A \) corrisponderebbe all’insieme vuoto e di conseguenza \( A \) e \( \mathcal{C}_UA \) non costituirebbero una partizione per \( U \).
Esempio (costruire una partizione di un insieme)
Sia assegnato l’insieme \( A = \{1,2,3,4\} \). Una possibile partizione dell’insieme \( A \) è costituita dagli insiemi:
\[ A_1=\{1,2 \}, \quad A_2 = \{3, 4\} \]
Infatti, indicando genericamente il numero in pedice con il numero naturale \( i \), osserviamo che:
- ciascun \( A_i \) è diverso dall’insieme vuoto;
- gli insiemi sono tra loro disgiunti, infatti \( A_1 \cap A_2 = \emptyset \). Ciò è ovvio perché i due insiemi non hanno elementi in comune;
- l’unione degli insiemi di tale partizione fornisce come risultato l’insieme di partenza. Infatti, \( A_1 \cup A_2 = \{1,2\}\cup\{3,4\} = \{1,2,3,4\} \).
Osserviamo che questa non è l’unica partizione possibile per l’insieme \( A \). Infatti, anche i seguenti tre insiemi:
\[ A_1 = \{1\}, \quad A_2=\{2,3\}, \quad A_3=\{4\} \]
costituiscono ugualmente una partizione dell’insieme \( A \) (lascio a voi il compito di verificarlo, come abbiamo fatto per la precedente partizione).
Invece, per l’insieme \( B = \{1,2\} \) , oltre alla partizione banale in cui l’unico sottoinsieme (improprio) è \( B \) stesso, è possibile soltanto una partizione, costituita dai seguenti sottoinsiemi propri di \( B \):
\[ B_1 = \{1\},\quad B_2 = \{2\} \]
In generale, dunque, vediamo come le possibilità che abbiamo di scrivere differenti partizioni per un insieme dipende da quanti elementi ha l’insieme stesso. Ora, ha perfettamente senso chiedersi se esiste una regola per stabilire quante possibili partizioni esistano per un dato insieme finito. Questa esiste, ma la sua trattazione va un po’ oltre rispetto ai nostri obiettivi. Però sappiate che c’è 😉
Per gli insiemi infiniti, invece, la risposta è secca: le possibili partizioni di un insieme infinito sono infinite.
Insiemi infiniti e partizioni
Negli esempi visti abbiamo scritto una possibile partizione per insiemi finiti, cioè costituiti da un numero finito di elementi. Gli insiemi infatti erano rappresentati per elencazione.
Consideriamo ora l’insieme \( \mathbb{Z} \) di tutti i numeri relativi (cioè, l’insieme di tutti i numeri interi positivi e negativi, più lo zero). E possibile scriverne almeno una partizione?
Sicuramente. Ad esempio, i seguenti insiemi costituiscono una partizione per \( \mathbb{Z} \):
\[ A=\{x \in \mathbb{Z} \quad \text{t.c} \quad x < 0\}; \qquad B = \{x \in \mathbb{Z} \quad \text{t.c} \quad x \geq 0\} \]
ove \( A \) è l’insieme dei numeri relativi minori di \( 0 \) e \( B \) è l’insieme dei numeri relativi maggiori o uguali a \( 0 \).
Ora, ciascun insieme ha evidentemente almeno un elemento.
Inoltre, gli insiemi sono tra loro disgiunti. Infatti, la loro intersezione è pari all’insieme vuoto poiché non hanno elementi in comune.
Infine, l’unione degli insiemi ha come risultato l’insieme di partenza. Abbiamo dunque verificato le condizioni per cui tale gruppo di sottoinsiemi di \( \mathbb{Z} \) costituisce una partizione di \( \mathbb{Z} \).
Osserviamo che se avessimo scritto i due sottoinsiemi di \( \mathbb{Z} \) nel seguente modo:
\[ A=\{x \in \mathbb{Z} \quad \text{t.c} \quad x < 0\}; \qquad B = \{x \in \mathbb{Z} \quad \text{t.c} \quad x > 0\} \]
essi non avrebbero costituito una partizione per \( \mathbb{Z} \). Infatti, se osservate attentamente le proprietà caratteristiche dei due insiemi, vi renderete immediatamente conto che lo zero è escluso da entrambi gli insiemi. E siccome lo zero appartiene a \( \mathbb{Z} \), i due insiemi non possono di certo essere una sua partizione. Viene meno infatti, il requisito che l’unione dei sottoinsiemi della partizione deve avere come risultato l’insieme di partenza (cioè, in questo caso, \( \mathbb{Z} \)).
Anche se avessimo definito i due sottoinsiemi come:
\[ A=\{x \in \mathbb{Z} \quad \text{t.c} \quad x \leq 0\}; \qquad B = \{x \in \mathbb{Z} \quad \text{t.c} \quad x \geq 0\} \]
essi non avrebbero rappresentato comunque una partizione per \( \mathbb{Z} \). Infatti, la loro unione è sì \( \mathbb{Z} \), ma i due insiemi non sono tra loro disgiunti (infatti, poiché è stato usato il simbolo di “minore o uguale” in entrambe le rispettive proprietà caratteristiche, i due insiemi hanno come elemento comune lo zero!).
Quest’ultimo esempio è molto importante. Nel corso degli studi vi capiterà spesso di dover suddividere un insieme infinito in sottoinsiemi che siano una partizione dell’insieme. Un uso oculato dei simboli di disuguaglianza è qui fondamentale. Il trucco è ricordarsi sempre di verificare che i simboli di disuguaglianza comprendano anche l’uguaglianza (cioè siano ad esempio un “minore o uguale”) solo quando necessario 😉
Torniamo ora agli insiemi finiti e svolgiamo insieme il seguente esercizio.
Esercizio
Scrivere tutte le possibili partizioni dell’insieme:
\[ A=\{1,2,3\} \]
Indicheremo ciascuna partizione come una famiglia di insiemi. In altre parole, elencheremo tra parentesi graffe i sottoinsiemi che costituiscono una data partizione. Ad esempio, usando questa notazione, la partizione di \( A \) costituita dagli insiemi \( A_1 \) e \( A_2 \) sarà data da:
\[ \{A_1, \: A_2\} \]
Ora, cominciamo con l’esercizio. La più semplice partizione che possiamo scrivere è quella costituita dall’insieme stesso:
\[ \{A\} \]
Questa rappresenta per l’insieme dato l’unica possibile partizione ottenuta senza dividere in parti l’insieme.
Abbiamo poi le seguenti partizioni, tutte costituite da sottoinsiemi propri di \( A \). Cominciamo con:
\[ \{A_1, A_2, A_3 \} \quad \text{con} \quad A_1=\{1\}, \: A_2 = \{2\}, \: A_3=\{3\} \]
Si tratta dell’unica partizione possibile dividendo l’insieme in tre parti. Abbiamo poi tre ulteriori partizioni, ciascuna ottenuta dividendo l’insieme in due parti:
\[ \{A_1, A_4\} \quad \text{con} \quad A_1 =\{1\}, \: A_4=\{2,3\} \]
\[ \{A_5, A_3\} \quad \text{con} \quad A_5=\{1,2\}, \: A_3=\{3\} \]
\[ \{A_6, A_2\} \quad \text{con} \quad A_6=\{3,1\}, \: A_2=\{2\} \]
Osservando che l’ordine di elencazione non conta, ci rendiamo conto che abbiamo esaurito tutte le combinazioni possibili 😉 Tentando di scrivere altre partizioni, incorreremmo nell’errore di scrivere sottoinsiemi la cui intersezione è diversa dall’insieme vuoto. Dunque, attenzione: questo non è l’insieme potenza.
Per l’insieme dato sono dunque possibili, in totale, cinque differenti partizioni.
La lezione sul concetto di partizione di un insieme termina qui 🙂 Nella prossima lezione vedremo il prodotto cartesiano. Ciao!
