Definizione intuitiva
Rimandiamo la definizione formale a qualche paragrafo più in basso. Pensiamo ora a cosa vuol dire “limite infinito di una funzione per \( x \) che tende ad infinito” in spiccioli 😉
Prendiamo una funzione che conosciamo bene e che ci ha aiutato molto nel risolvere le disequazioni di secondo grado: la parabola.
Questa funzione è definita su tutti i reali ed ha valori in tutto \( \mathbb{R} \). Quindi, siamo liberi di prendere un qualsiasi valore sull’asse delle \( x \) e calcolare per esso un valore nell’asse delle \( y \).
E’ interessante provare a vedere come si comporta la funzione per valori della \( x \) crescenti, cioè sempre più grandi. Non è troppo difficile notare che è possibile far crescere la \( x \) quanto ci pare, prendendo valori grandissimi, ottenendo corrispondenti valori della \( y \) sempre più grandi. E’ dunque chiaro, osservando anche il grafico, che per valori della \( x \) tendenti ad infinito, anche la funzione assumerà valori tendenti all’infinito.
Vediamo anche che facendo tendere la \( x \) a valori negativi sempre più grandi in modulo, la \( y \) tenderà verso valori positivi sempre più grandi. E qui osserviamo che, facendo tendere la \( x \) a \( -\infty \), la \( y \) tende a \( +\infty \). Il fatto che pur facendo tendere la \( x \) a \( -\infty \) otteniamo comunque valori tendenti a \( +\infty \) per la \( y \) è dovuto semplicemente al fatto che nella funzione abbiamo il quadrato (ormai dovremmo sapere bene che meno per meno fa più) 😉
Nel caso della funzione \( y=x^3 \) è abbastanza facile intuire che per valori della \( x \) tendenti a \( -\infty \) anche la funzione tenderà a \( -\infty \). Il grafico ci dà conferma di questo:
Vi ricordate i casi del limite finito di una funzione per \( x\to\infty \) e del limite infinito di una funzione per \( x \) che tende ad un valore finito?
\[ \lim_{x \to +\infty}f(x) = l; \qquad \lim_{x \to x_0}f(x) = +\infty \]
Nota: ipotizziamo per ora il segno positivo per la quantità “infinito” in entrambi i casi.
Proviamo a definire brevemente le condizioni di limite per questi due casi (che già conosciamo).
Nel primo caso, diremo che il limite esiste finito se fissato un qualunque \( \epsilon \) positivo è possibile determinare per esso un \( k_\epsilon \) anch’esso positivo tale che \( \forall \: x > k_\epsilon \) risulti \( \left|f(x)-l\right| < \epsilon \).
Nel secondo caso, diremo che il limite della funzione è infinito se, fissato un \( M \) positivo è possibile determinare in corrispondenza di esso un \( \delta_M \) anch’esso positivo tale che, per ogni \( x \) che non sia \( x_0 \)e rispettante la condizione \( \left|x-x_0\right|<\delta_M \), risulti \( f(x)>M \).
Ora, il caso che stiamo studiando può essere visto come un ibrido tra i due casi precedenti 😉 Infatti, siccome il limite è infinito (abbiamo ipotizziamo \( +\infty \)), certamente dovrà risultare \( f(x)>M \). Inoltre, siccome la \( x \) tende a più infinito, la condizione di limite appena espressa, se questo esiste ed è infinito, dovrà essere verificata per ogni \( x>k_M \) (avendo come al solito fissato un \( M > 0 \) e scelto in corrispondenza di esso un \( k_M \) anch’esso positivo).
Ora, mettendo insieme i discorsi empirici fatti con i grafici e le definizioni rigorose appena rispolverate, dovrebbe risultare chiara la seguente definizione rigorosa 🙂
Limite più infinito di una funzione per x che tende a più infinito
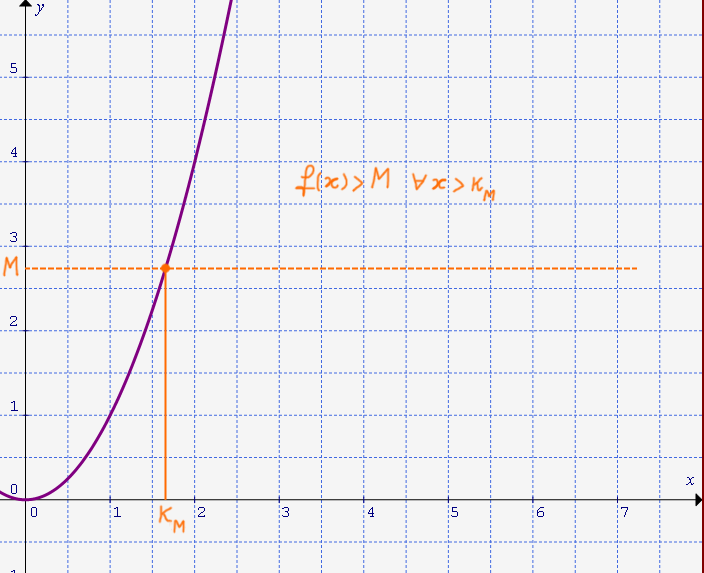
Prendiamo una funzione \( f(x) \) definita in un insieme \( D_f \) illimitato superiormente, cioè ad esempio del tipo \( D_f=[a, \quad +\infty), \quad a \in \mathbb{R} \). Possiamo dire che:
\[ \lim_{x \to +\infty}f(x)=+\infty \]
se, fissato un qualsiasi \( M>0 \), è possibile determinare in corrispondenza di esso un \( k_M>0 \) tale che, per ogni \( x \) che appartiene a \( D_f \) e che verifica la condizione \( x > k_M \) risulti:
\[ f(x)>M \]
Questa condizione di limite è soddisfatta ad esempio dalla funzione \( y=x^2 \) sul primo quadrante:
Ovviamente osservare il solo grafico non è sufficiente per affermare che:
\[ \lim_{x \to +\infty}x^2=+\infty \]
E’ necessaria una verifica rigorosa che vedremo più avanti 😉
Ora, “divertendoci” a cambiare i segni delle quantità infinite abbiamo altri tre casi, del tutto simili al precedente. Come vedrete non è necessario impararli a memoria.
Come prima cosa bisogna ragionare sui segni e rendersi conto che in base ad essi cambiano gli operatori maggiore o minore nelle relazioni della definizione 😉 Inoltre, è anche da osservare che se la \( x \) tende a \( -\infty \), il dominio della funzione \( D_f \) dovrà essere illimitato inferiormente (cioè essere ad esempio del tipo \( D_f=(-\infty, a], \quad a \in \mathbb{R} \)). Ciò è intuitivo, poiché pretendiamo che la funzione possa essere calcolata in tutte le \( x \) lungo la direzione negativa a partire da un certo valore della \( x \).
Limite meno infinito di una funzione per x che tende a meno infinito
Prendiamo una funzione \( f(x) \) definita in un insieme \( D_f \) illimitato inferiormente, cioè ad esempio del tipo \( D_f=(-\infty, \: a], \quad a \in \mathbb{R} \). Possiamo dire che:
\[ \lim_{x \to -\infty}f(x)=-\infty \]
se, fissato un qualsiasi \( M>0 \), è possibile determinare in corrispondenza di esso un \( k_M>0 \) tale che, per ogni \( x \) che appartiene a \( D_f \) e che verifica la condizione \( x < k_M \) risulti:
\[ f(x)<M \]
Un esempio pratico è dato dalla funzione \( f(x)=x^3 \) sul terzo quadrante:
Ora, rimangono solo due casi 🙂
Limite più infinito di una funzione per x che tende a meno infinito
Prendiamo una funzione \( f(x) \) definita in un insieme \( D_f \) illimitato inferiormente, cioè ad esempio del tipo \( D_f=(-\infty, \: a], \quad a \in \mathbb{R} \). Possiamo dire che:
\[ \lim_{x \to -\infty}f(x)=+\infty \]
se, fissato un qualsiasi \( M>0 \), è possibile determinare in corrispondenza di esso un \( k_M>0 \) tale che, per ogni \( x \) che appartiene a \( D_f \) e che verifica la condizione \( x < k_M \) risulti:
\[ f(x)>M \]
Un esempio di funzione che si comporta in questo modo è dato da \( y=x^2 \) nel secondo quadrante:
Coraggio, siamo all’ultimo caso 🙂
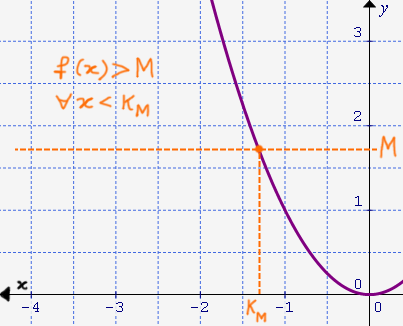
Limite meno infinito di una funzione per x che tende a più infinito
Prendiamo una funzione \( f(x) \) definita in un insieme \( D_f \) illimitato superiormente, cioè ad esempio del tipo \( D_f=[a, +\infty)], \quad a \in \mathbb{R} \). Possiamo dire che:
\[ \lim_{x \to +\infty}f(x)=-\infty \]
se, fissato un qualsiasi \( M>0 \), è possibile determinare in corrispondenza di esso un \( k_M>0 \) tale che, per ogni \( x \) che appartiene a \( D_f \) e che verifica la condizione \( x > k_M \) risulti:
\[ f(x)<M \]
Un esempio di questo comportamento è dato dalla funzione \( y=-x^2 \) sul quarto quadrante:
Precisazioni sul dominio delle funzioni nei casi esaminati
Nelle definizioni, abbiamo richiesto a seconda dei casi un dominio almeno illimitato superiormente o inferiormente 🙂 Per chiarire meglio le idee, prendiamo uno dei casi visti, ad esempio:
\[ \lim_{x \to +\infty}f(x) = +\infty \]
Come sappiamo, siccome la \( x \) tende a più infinito, e quindi deve essere “libera di muoversi” lungo la direzione positiva dell’asse \( x \) potendo sempre attribuire un corrispondente valore alla funzione, il dominio dovrà essere illimitato superiormente.
Precisiamo meglio: la \( x \) dovrà essere “libera di muoversi” lungo la direzione positiva dell’asse \( x \) da un certo punto in poi. Ciò vuol dire che da questo punto in poi la funzione sarà definita in qualunque \( x \) grande quanto vogliamo. La \( x \) potrà dunque tendere a più infinito.
Il concetto “da un certo punto in poi” lo abbiamo tradotto dicendo che \( D_f \) (il dominio della funzione) può essere del tipo:
\[ D_f = [a, \: +\infty), \: a \in \mathbb{R} \]
Ci tengo però a fare una precisazione. Il fatto che il dominio sia illimitato superiormente è in questo caso una condizione necessaria affinché abbia senso scrivere \( x \to +\infty \). Tuttavia, il dominio può anche essere illimitato sia superiormente, sia inferiormente. Come dire, ci occorre che sia illimitato superiormente, ma se anche lo è inferiormente, non abbiamo problemi 😉
Così, sempre per il caso in esame:
\[ \lim_{x \to +\infty}f(x) = +\infty \]
potremo anche avere ad esempio:
\[ D_f = (-\infty, k]\: \cup \: [a, \: +\infty) \]
Anche l’intero insieme dei numeri reali soddisfa il requisito richiesto. Infatti, esso è certamente illimitato superiormente. Lo è anche inferiormente, è ovvio: questo non ci serve, ma non crea problemi. Per cui può anche essere:
\[ D_f = \mathbb{R} \]
\( D_f \) può inoltre essere del tipo:
\[ D_f = \mathbb{R} – \{k\}, \: k \in \mathbb{R} \]
Cioè può essere anche l’insieme dei reali privato di un elemento.
Prendiamo ad esempio la funzione:
\[ f(x) = \dfrac{x^2-3}{x} \]
Essa ha come dominio:
\[ D_f = \mathbb{R} – \{0\} \]
Ha dunque senso chiedersi che limite ha la funzione per \( x \to +\infty \)? Sì, perché \( D_f \) è illimitato superiormente. Come caratteristica in più, lo è anche inferiormente, e ciò non ci da alcun problema.
In più, essendo il dominio illimitato anche inferiormente, ha pure senso chiedersi che limite ha la funzione per \( x \to -\infty \)🙂
Si può dimostrare rispettivamente che:
\[ \lim_{x \to +\infty}\dfrac{x^2-3}{x}=+\infty \]
e che:
\[ \lim_{x \to -\infty}\dfrac{x^2-3}{x}=-\infty \]
Nella prossima lezione, vedremo come verificare questi risultati. Più avanti, vedremo come calcolarli.
Ciao a tutti e buono studio con Altramatica! 🙂