Può succedere ad esempio che una funzione non sia definita per valori anche di poco più grandi di \( x_0 \) ma sia definita solo per valori più piccoli di \( x_0 \). Oppure, può succedere che per valori di poco più grandi di \( x_0 \) la funzione tenda ad un valore, mentre per valori di poco più piccoli di \( x_0 \) essa tenda ad un altro valore. In questi casi, pur non esistendo il limite nel punto \( x_0 \) come lo abbiamo visto finora, ha senso comunque studiare il comportamento della funzione in prossimità di \( x_0 \). A tale scopo, è necessario introdurre le definizioni di limite destro e limite sinistro di una funzione.
Limite destro e limite sinistro di una funzione: concetti preliminari
Le definizioni di limite destro e limite sinistro di una funzione non sono altro che una particolarizzazione di definizioni che abbiamo già studiato. Ma andiamo in ordine 😉
Consideriamo solo casistiche nelle quali la \( x \) tenda sempre e soltanto ad una certo valore finito (cioè \( x \rightarrow x_0 \), con \( x_0 \: \in \: \mathbb{R} \)). Ora, richiamiamo brevemente le definizioni di limite che già conosciamo.
Dire che una funzione \( f(x) \), definita in un intervallo \( I(x_0) \) dell’insieme dei numeri reali, privato del punto \( x_0 \), ammette limite finito per \( x\: \rightarrow \: x_0 \), significa che per ogni \( x \) appartenente a tale intervallo, una volta scelto un certo valore \( \epsilon \) piccolo quanto si vuole, è sempre possibile determinare per \( \epsilon \)stesso un valore \( \delta \) tale che, per ogni x che verifica la condizione \( x_0-\delta<x<x_0+\delta, \quad x \neq x_0 \), risulta che \( |f(x)-l|<\epsilon \).
Ora, ricordiamo che la condizione \( x_0-\delta<x<x_0+\delta, \quad x \neq x_0 \) equivale all’affermare che la \( x \) appartiene all’intorno \( I=]x_0-\delta, \: x_0+\delta[-\{x_0\} \). Ora, cosa succede invece se la condizione di limite \( |f(x)-l| \) è verificata solo per \( x\in \: ]x_0-\delta, \: x_0[ \) o è verificata solo per \( x \in ]x_0, \: x_0+\delta[ \)?
Ci chiediamo cioè cosa succede quando la condizione di limite è rispettata solo dalle \( x \) che appartengono rispettivamente ad un intorno sinistro o ad un intorno destro di \( x_0 \).
Detta in linguaggio comune, ci chiediamo cioè cosa succede se una funzione ammette limite in un punto solo per valori più piccoli di quel punto, e che cosa succede se una funzione ammette invece limite in un punto solo per valori più grandi di quel punto.
Nel primo caso, diremo che la funzione ammette limite sinistro in quel punto, nel secondo caso diremo invece che ammette limite destro.
Per vedere se una funzione ammette limite sinistro, si studia la funzione per valori che si approssimano sempre più ad \( x_0 \) da sinistra. Cioè, ci si avvicina con le \( x \) sempre più ad \( x_0 \) partendo da valori più piccoli di \( x_0 \).
Allo stesso modo, per vedere se una funzione ammette limite destro, si studia la funzione per valori che si approssimano sempre più ad \( x_0 \) da destra. Ci si avvicina cioè sempre più ad \( x_0 \) partendo da valori più grandi di \( x_0 \).
Vediamo ora degli esempi osservando grafici di funzioni. Un esempio classico è quello di funzioni che hanno un “gradino”, ossia un brusco cambiamento del valore assunto per valori della \( x \) tra loro “molto vicini”.
Consideriamo ad esempio la funzione:
\[ y = \frac{\left| sin(x) \right|}{x} \]
Vediamo come si comporta graficamente:
Appare chiaro che la funzione non ammette limite nel punto \( x_0=0 \), poiché la funzione non tende ad uno stesso valore quando le \( x \) tendono a \( x_0 \) da sinistra e da destra. Tuttavia, i limiti sinistro e destro esistono entrambi. In particolare, la funzione ha limite sinistro in \( x_0=0 \) pari a -1, ed ha limite destro in \( x_0=0 \) pari a 1.
Infatti, per tutte le \( x \) che appartengo ad un intorno sinistro di \( x_0 \), la funzione assume valori che si approssimano sempre di più a -1 (di qui il limite sinistro pari a -1).
In modo simile, per tutte le \( x \) che appartengo ad un intorno destro di \( x_0 \), la funzione assume valori che si approssimano sempre di più a 1 (di qui il limite destro pari a 1).
Veniamo ora alle definizioni formali nei vari casi 🙂 Ricordiamo che vale ancora un importante requisito per il punto \( x_0 \), è cioè che questi sia un punto di accumulazione per il dominio della funzione. Ciò significa, ripetiamolo, che attorno ad esso devono cadere infiniti punti del dominio 😉
Limite finito destro di una funzione
Sia data una funzione \( f \) definita in un intorno destro di \( x_0 \), che indichiamo con \( I^+(x_0) \). Consideriamo l’intorno privato del punto \( x_0 \). Quindi l’intorno è rappresentato dall’insieme \( I^+(x_0)=]x_0, \: x_0+\delta[ \).
Si dice che la funzione ammette limite destro finito in \( x_0 \), e si scrive:
\[ lim_{x \to x_0^+}f(x)=l, \qquad l\in \mathbb{R} \]
se, fissato a piacere un numero \( \epsilon > 0 \), è possibile determinare per esso un numero \( \delta>0 \) tale che, per ogni \( x \in I^+(x_0) \) e verificante la condizione \( x_0<x<x_0+\delta \), risulta:
\[ |f(x)-l|<\epsilon \]
Osserviamo che, nella definizione, la condizione \( x_0<x<x_0+\delta \) può essere riscritta in maniera diversa. Essa equivale infatti a due distinte disequazioni messe a sistema:
\[ \begin{cases}x>x_0\\ \\ x< x_0+\delta\end{cases} \]
e quindi:
\[ \begin{cases} x-x_0>0 \\ \\ x-x_0<\delta\\ \end{cases} \]
Si può dunque concludere che la condizione \( x_0<x<x_0+\delta \) equivale a \( 0<x-x_0<\delta \). Questa è la condizione che più spesso si trova nei libri 🙂 Ho però preferito la formulazione alternativa riportata nella “mia” definizione poiché molto più intuitiva.
Se facciamo un piccolo salto indietro, dovremmo riuscire a ricordarci che nella definizione di limite finito di un punto, avevamo la condizione per i valori della \( x \), \( 0<|x-x_0|<\delta \). Ora, tale condizione è quasi identica a quella che abbiamo appena trovato. L’unica differenza è data dal modulo. Come mai questo? Ebbene, nel caso del limite destro è chiaro che il modulo va tolto. Infatti, poiché nel processo di limite la \( x \) parte da valori più grandi di \( x_0 \), cioè valori tutti appartenenti ad un intorno destro di \( x_0 \), siamo certi che la differenza \( x-x_0 \) sarà sempre positiva. Di qui l’assenza del modulo nella condizione di appartenenza relativa ai valori delle \( x \) nel caso del limite destro 🙂
Limite finito sinistro di una funzione
Sia data una funzione \( f \) definita in un intorno sinistro di \( x_0 \), che indichiamo con \( I^-(x_0) \). Consideriamo l’intorno privato del punto \( x_0 \). Quindi l’intorno è rappresentato dall’insieme \( I^-(x_0)=] x_0-\delta, \: x_0[ \).
Si dice che la funzione ammette limite sinistro finito in \( x_0 \), e si scrive:
\[ lim_{x \to x_0^-}f(x)=l, \qquad l\in \mathbb{R} \]
se, fissato a piacere un numero \( \epsilon > 0 \), è possibile determinare per esso un numero \( \delta>0 \) tale che, per ogni \( x \in I^-(x_0) \) e verificante la condizione \( x_0-\delta<x \: < \: x_0 \)risulta:
\[ |f(x)-l|<\epsilon \]
Osserviamo che, anche in questa definizione, la condizione relativa alle \( x \) può essere riscritta in maniera diversa. Essa equivale infatti a due distinte disequazioni messe a sistema:
\[ \begin{cases}x>x_0-\delta\\ \\ x< x_0\end{cases} \]
e quindi:
\[ \begin{cases} x-x_0>-\delta \\ \\ x-x_0<0\\ \end{cases} \]
Si può dunque concludere che la condizione equivale a \( -\delta<x-x_0<0 \: \). Questa è la forma più usata nei libri.
Facendo di nuovo un salto indietro, osserviamo che nella definizione di limite finito in un punto, avevamo la condizione per i valori della \( x \), \( 0<|x-x_0|<\delta \). E’ possibile riesprimere questa condizione anche nel caso del limite sinistro. Infatti, essendo l’intorno del punto \( x_0 \) sinistro, la differenza \( x-x_0 \) è senz’altro negativa. Quindi possiamo togliere i simboli di modulo dalla precedente relazione, a patto di invertire il segno degli argomenti della funzione modulo:
\( x-x_0<0\: \Rightarrow \: 0<|x-x_0|<\delta \iff \: 0<-x+x_0<\delta \)
Esprimiamo l’ultima espressione ottenuta come un sistema:
\[ \begin{cases} -x+x_0>0 \\ \\ -x+x_0<\delta \end{cases} \]
e quindi, invertendo i segni:
\[ \begin{cases} x-x_0<0 \\x-x_0>-\delta \\ \end{cases} \]
E siamo arrivati (era ora!), perché da questa otteniamo immediatamente la condizione: \( -\delta<x-x_0<0 \).
Data quindi la possibilità di particolarizzare la condizione sulle \( x \) del limite generico al caso del limite sinistro, possiamo vedere come anche il limite sinistro non sia altro che un caso particolare del limite “generico”. 🙂
Limiti infiniti destro e sinistro di una funzione
Ci rimangono ora da studiare i casi di limiti destro e sinistro il cui risultato è infinito.
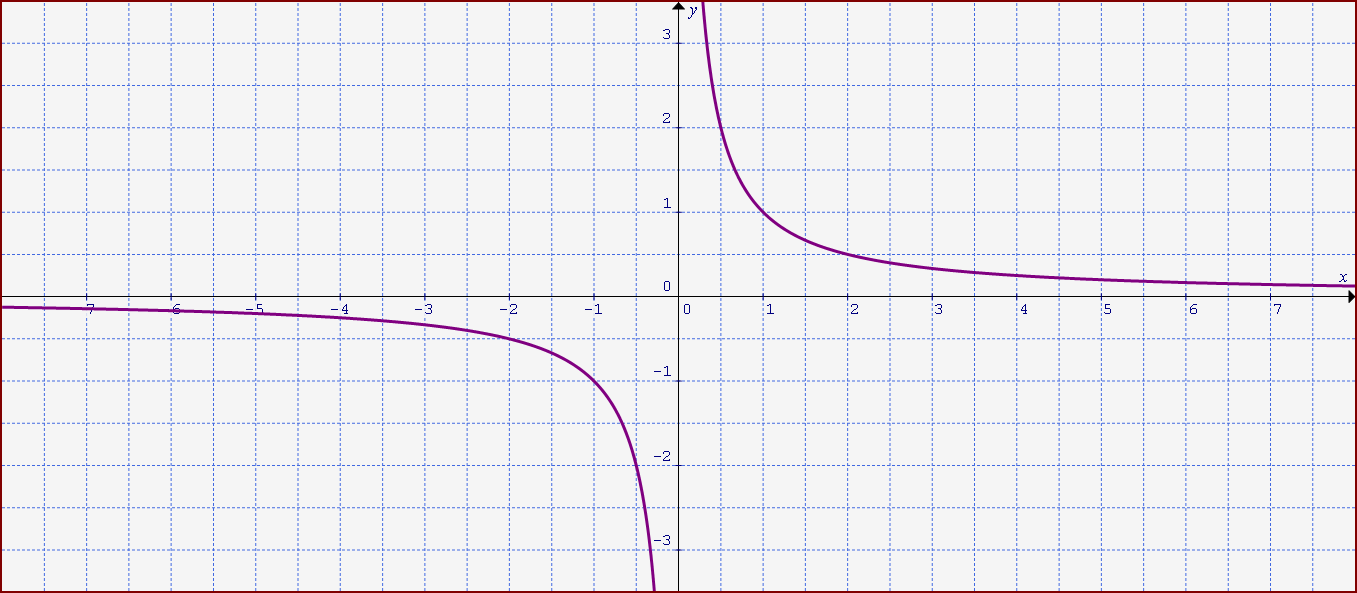
Consideriamo ad esempio la funzione:
\[ f(x)=\dfrac{1}{x} \]
Come possiamo vedere, essa in 0 non è definita. Tuttavia, è agevole notare che per valori delle \( x \) di poco più piccoli di 0, la funzione assume valori negativi grandissimi in modulo. Allo stesso modo, è altrettanto immediato notare che per valori di poco più grandi di 0 la funzione assume valori positivi grandissimi in modulo.
In altri termini, diciamo che per la \( x \) che tende a \( x_0=0 \) da sinistra, cioè a partire da valori più piccoli di \( x_0 \), la funzione tende a \( -\infty \). Invece, diciamo che per la \( x \) che tende a \( x_0=0 \) da destra, cioè a partire da valori più grandi di \( x_0 \), la funzione tende a \( +\infty \).
E quindi, sfruttando le definizioni di limite destro e sinistro che abbiamo introdotto poco fa, diremo che:
\[ \lim_{x \to 0^-}\dfrac{1}{x}=-\infty \]
e che:
\[ \lim_{x \to 0^+}\dfrac{1}{x}=+\infty \]
Ora che abbiamo chiarito di cosa vogliamo parlare, è bene che richiamiamo la definizione di limite infinito di una funzione per \( x \) che tende ad un valore reale \( x_0 \) 🙂 Consideriamo per ora il caso di limite \( +\infty \).
Sia \( f(x) \) una funzione definita in un intorno \( I \) di \( x_0 \), privato al più del punto \( x_0 \).
Diciamo che il limite per \( x \) che tende ad \( x_0 \) della funzione è più infinito, e si scrive:
\[ \lim_{x \to x_0}{f(x)}=+\infty \]
se, comunque fissato un \( M \), è possibile trovare un corrispondente \( \delta_M > 0\) tale che, per ogni \( x \in I \) che soddisfa la condizione
\[ |x-x_0|<\delta_M, \quad x \neq x_0 \qquad (*) \]
risulta:
\[ f(x)>M \]
Limite infinito destro di una funzione
Per introdurre la definizione di limite (più) infinito destro di una funzione in un punto \( x_0 \), analizziamo la condizione (*) della precedente definizione e vediamo di adattarla al nostro caso.
Osserviamo che volendo ora studiare un limite destro, le \( x \) appartengono tutte ad un intorno destro di \( x_0 \). Dunque, siamo sicuri che la differenza \( |x-x_0| \) sarà sempre positiva. Si tratta dunque di adattare la precedente definizione effettuando semplicemente pochi “ritocchi”, tra i quali togliere il simbolo di modulo nella condizione data per le \( x \) 😉
Via!
Definizione (caso più infinito). Sia data una funzione \( f(x) \) definita in un intorno destro di \( x_0 \), che chiameremo \( I^+(x_0) \), privato del punto \( x_0 \). Si dice che la funzione ha limite più infinito per \( x \) che tende ad \( x_0 \) da destra, e si scrive:
\[ \lim_{x \to x_0^+}f(x)=+\infty \]
se, scelto comunque un valore \( M\), è possibile determinare in corrispondenza di esso un numero \( \delta_M>0 \) tale che, per ogni \( x \) appartenente all’intorno \( I^+(x_0) \) e verificante la condizione \( x-x_0<\delta_M, \quad x\neq 0 \) risulta:
\[ f(x)>M \]
E’ evidente la possibilità di adattare la definizione al caso meno infinito. Si tratta semplicemente di introdurre il simbolo \( -\infty \) e di invertire il simbolo di disuguaglianza sulla condizione di limite relativa ad \( f(x) \). Ma vediamolo esplicitamente 🙂
Definizione (caso meno infinito). Sia data una funzione \( f(x) \) definita in un intorno destro di \( x_0 \), che chiameremo \( I^+(x_0) \), privato del punto \( x_0 \). Si dice che la funzione ha limite meno infinito per \( x \) che tende ad \( x_0 \) da destra, e si scrive:
\[ \lim_{x \to x_0^+}f(x)=-\infty \]
se, scelto comunque un valore \( M\), è possibile determinare in corrispondenza di esso un numero \( \delta_M>0 \) tale che, per ogni \( x \) appartenente all’intorno \( I^+(x_0) \) e verificante la condizione \( x-x_0<\delta_M, \quad x \neq 0 \) risulta:
\[ f(x)<M \]
Limite infinito sinistro di una funzione
Riprendiamo ancora la condizione sulle \( x \) nella definizione di limite infinito di una funzione in un punto, indicata con (*) e che per comodità riportiamo nuovamente:
\[ |x-x_0|<\delta_M, \quad x \neq x_0 \qquad (*) \]
Nel caso di limite infinito sinistro, la differenza \( x-x_0 \) sarà sempre negativa, poiché le \( x \) vivono in un intorno sinistro del punto \( x_0 \). Quindi, dovremo riscrivere la condizione (*) togliendo il simbolo del modulo ed invertendo i segni dell’argomento del modulo:
\[ -x+x_0<\delta_M, \quad x \neq 0 \]
ovvero:
\[ x_0-x<\delta_M, \quad x \neq 0 \]
Ora, questa è la condizione per le \( x \) da usare nel caso di limite infinito sinistro (più e meno infinito).
Definizione (caso più infinito). Sia data una funzione \( f(x) \) definita in un intorno sinistro di \( x_0 \), che chiameremo \( I^-(x_0) \), privato del punto \( x_0 \). Si dice che la funzione ha limite più infinito per \( x \) che tende ad \( x_0 \) da sinistra, e si scrive:
\[ \lim_{x \to x_0^-}f(x)=+\infty \]
se, scelto comunque un valore \( M\), è possibile determinare in corrispondenza di esso un numero \( \delta_M>0 \) tale che, per ogni \( x \) appartenente all’intorno \( I^-(x_0) \) e verificante la condizione \( x_0-x<\delta_M, \quad x \neq 0 \) risulta:
\[ f(x)>M \]
Possiamo agevolmente estendere la definizione al caso di limite pari a meno infinito.
Definizione (caso meno infinito). Sia data una funzione \( f(x) \) definita in un intorno sinistro di \( x_0 \), che chiameremo \( I^-(x_0) \), privato del punto \( x_0 \). Si dice che la funzione ha limite meno infinito per \( x \) che tende ad \( x_0 \) da sinistra, e si scrive:
\[ \lim_{x \to x_0^-}f(x)=-\infty \]
se, scelto comunque un valore \( M\), è possibile determinare in corrispondenza di esso un numero \( \delta_M>0 \) tale che, per ogni \( x \) appartenente all’intorno \( I^-(x_0) \) e verificante la condizione \( x_0-x<\delta_M, \quad x \neq 0 \) risulta:
\[ f(x)<M \]
Nella prossima lezione, vedremo come verificare l’esistenza di un limite proprio utilizzando i limiti destro e sinistro.