Ci occupiamo ora della tecnica di integrazione per sostituzione, relativamente al caso degli integrali indefiniti. Per chi è invece in fase di ripasso ed è interessato alla tecnica di integrazione per sostituzione inerente agli integrali definiti, è disponibile la lezione dedicata. Chi invece sta studiando la tecnica di integrazione per sostituzione dall’inizio, può tranquillamente proseguire la lettura di questa lezione.
Come per la tecnica di integrazione per parti, ci proporremo di ricavare la regola dell’integrazione per sostituzione partendo dai risultati ottenuti nello studio delle derivate.
Nella scorsa lezione abbiamo ricavato la tecnica di integrazione per parti sfruttando la regola della derivata del prodotto. Ora ricaveremo la tecnica di integrazione per sostituzione a partire dalla regola della derivata della funzione composta. Lo strumento che ricaveremo sarà particolarmente potente poiché otterremo due formule di integrazione per sostituzione (prima specie e seconda specie).
Fatte le dovute premesse vediamo subito come ricavare ed utilizzare la regola di integrazione per sostituzione.
NOTA: a chi già conosce gli integrali definiti, consigliamo di leggere successivamente anche la lezione sugli integrali definiti per sostituzione.
Integrazione per sostituzione
Per introdurre la tecnica di integrazione per sostituzione è anzitutto necessario ricordare la regola della derivata della funzione composta:
\[ \dfrac{d}{dx}F(g(x)) = \dfrac{d}{du}F(u)\cdot \dfrac{d}{dx}(g(x)), \qquad \text{con} \quad g(x)=u \]
Consideriamo in particolare la funzione composta \( F(g(x)) \) ove la funzione esterna \( F(x) \) è un’antiderivata per \( f(x) \). Tale convenzione risulterà utile per introdurre la regola di integrazione per sostituzione.
Procediamo passando agli integrali in entrambi i membri dell’uguaglianza appena scritta:
\[ \int \dfrac{d}{dx}F(g(x)) \, dx = \int \left[ \dfrac{d}{du}F(u)\cdot \dfrac{d}{dx}(g(x)) \right] \, dx \]
Osserviamo che l’integrazione e la derivazione sono operazioni tra loro inverse a meno di una costante additiva. Per cui riscrivendo di conseguenza il primo membro si ha:
\[ F(g(x)) + c = \int \left[ \dfrac{d}{du}F(u)\cdot \dfrac{d}{dx}(g(x)) \right] \, dx \]
Ora è opportuno osservare che \( \dfrac{d}{du}F(u) \) altri non è che la derivata di \( F(g(x)) \) rispetto all’argomento \( g(x) \). Indicando tale derivata come \( F'(g(x)) \) si ha:
\[ F(g(x)) + c = \int \left[F'(g(x))\cdot \dfrac{d}{dx}(g(x)) \right] \, dx \]
Come detto all’inizio, \( F(x) \) è un’antiderivata per \( f(x) \). Di conseguenza \( F'(g(x))=f(g(x)) \) e quindi:
\[ F(g(x)) + c = \int \left[f(g(x))\cdot \dfrac{d}{dx}(g(x)) \right] \, dx \]
Ora, al primo membro abbiamo la famiglia di tutte le antiderivate di \( f(g(x)) \). Questa per definizione corrisponde all’integrale indefinito \( \displaystyle \int f(u) \, du \) ponendo \( g(x)=u \). Pertanto possiamo scrivere:
\[ \int f(u) du= \int \left[f(g(x))\cdot \dfrac{d}{dx}(g(x)) \right] \, dx \]
E in conclusione, per la proprietà simmetrica dell’uguaglianza:
\[ \boxed{\int \left[f(g(x))\cdot \dfrac{d}{dx}(g(x)) \right] \, dx=\int f(u) du, \quad \text{con} \quad g(x)=u} \]
In altre parole, l’integrale indefinito rispetto alla variabile \( x \) di una funzione composta moltiplicata per la derivata dell’argomento è pari all‘integrale indefinito della funzione composta calcolato rispetto all’argomento della funzione composta stessa.
Quella appena presentata è la formula di integrazione per sostituzione della prima specie (o prima formula di integrazione per sostituzione).
Esempio sulla formula di integrazione per sostituzione di prima specie
Calcolare l’integrale indefinito:
\[ \int \sin (x^2) \cdot 2x \, dx \]
Osserviamo che dobbiamo integrare la funzione composta \( \sin (x^2) \) moltiplicata per \( 2x \), che è proprio la derivata dell’argomento della funzione composta stessa. Di conseguenza possiamo applicare la formula di integrazione per sostituzione della prima specie e si ha:
\[ \begin{align}&\int \sin (x^2) \cdot 2x \, dx = \left[\int \sin u \, du \right]_{x^2=u} = \\ \\ & = \left[-\cos(u)+c \right]_{x^2=u} \stackrel{u=x^2}{=}-\cos (x^2)+c, \quad c \in \mathbb{R} \end{align} \]
e questo è il risultato dell’integrale che dovevamo calcolare. 😉
Osserviamo che con scritture del tipo \( \displaystyle \left[\int \sin u \, du \right]_{x^2=u} \) intendiamo dire che è stata già eseguita la sostituzione \( x^2=u \), ovvero che tutti i termini \( x^2 \) sono stati sostituiti con la lettera \( u \). Indicando poi sopra l’uguale la sostituzione inversa \( u=x^2 \) vogliamo intendere che nel passaggio successivo sostituiamo a tutte le lettere \( u \) la quantità \( x^2 \). Tale sostituzione inversa è necessaria alla fine per poter esprimere il risultato in funzione di \( x \).
NOTA: l’uso della variabile ausiliaria \( u \) è necessario per poter indicare la variabile di integrazione con il simbolo \( du \), intendendo così l’integrale calcolato rispetto alla funzione \( g(x) \) e non rispetto alla variabile \( x \) come nei casi generali. In teoria si potrebbe evitare l’uso della variabile ausiliaria \( u \) utilizzando il simbolo \( d g(x) \), ma tale pratica è da evitare poiché un incremento infinitesimo viene scritto sempre rispetto ad una variabile (es., \( dx, \: dy, \: du \)) e mai rispetto ad una funzione indicata esplicitamente.
Tuttavia, una volta compreso che \( \displaystyle \int f(u)d u \) rappresenta l’integrale della funzione composta rispetto all’argomento della funzione composta stessa, è anche possibile saltare il cambio di variabile e scrivere direttamente:
\[ \int \sin (x^2) \cdot 2x \, dx = -\cos (x^2)+c, \quad c \in \mathbb{R} \]
Il ragionamento da fare è semplicemente questo: se l’integrale rispetto ad \( x \) di \( \sin x \) è pari a \( -\cos x+c \), allora l’integrale rispetto ad \( x^2 \) di \( \sin x^2 \) sarà per forza uguale a \( -\cos x^2 + c \). Ciò è del tutto simile a quanto abbiamo visto per la regola della derivata della funzione composta.
In ogni caso, continueremo ad indicare in modo rigoroso i cambi di variabile esplicitamente. 😉
Formula di integrazione per sostituzione della seconda specie
Riprendiamo la formula di integrazione per sostituzione della prima specie:
\[ \int \left[f(g(x))\cdot \dfrac{d}{dx}(g(x)) \right] \, dx= \left[ \int f(u) du\right]_{g(x)=u} \]
Supponiamo che \( g(x) \) sia invertibile. In tal caso, applichiamo ad entrambi i membri la sostituzione inversa \( x= g^{-1} (u) \):
\[ \left\{\int \left[f(g(x))\cdot \dfrac{d}{dx}(g(x)) \right] \, dx \right\}_{x=g^{-1}(u)}= \left\{ \left[ \int f(u) du\right]_{g(x)=u} \right\}_{x=g^{-1}(u)} \]
Lasciamo il primo membro così come è. Per le proprietà delle funzioni composte il secondo membro diventa semplicemente \( \displaystyle \int f(u) \, du \). Abbiamo così:
\[ \left\{\int \left[f(g(x))\cdot \dfrac{d}{dx}(g(x)) \right] \, dx \right\}_{x=g^{-1}(u)}= \int f(u) \, du \]
Per la proprietà simmetrica dell’uguaglianza cioè evidentemente equivale a scrivere:
\[ \int f(u) \, du = \left\{\int \left[f(g(x))\cdot \dfrac{d}{dx}(g(x)) \right] \, dx \right\}_{x=g^{-1}(u)} \]
Ora si tratta di aggiustare la formula ottenuta dal punto di vista formale. Poiché negli esercizi gli integrali di partenza da calcolare vengono espressi in funzione della \( x \), conviene scambiare le variabili \( x \) ed \( u \) tra loro. Si ha:
\[ \boxed{\int f(x) \, dx = \left\{\int \left[f(g(u))\cdot \dfrac{d}{du}(g(u)) \right] \, du \right\}_{u=g^{-1}(x)}} \]
e questa è la formula di integrazione per sostituzione della seconda specie (o seconda formula di integrazione per sostituzione).
Cerchiamo di capire l’utilità dell’uguaglianza appena ottenuta. 😉 La formula ci dice che è possibile integrare la funzione \( f(x) \) riconducendoci all’integrale di una funzione composta ove \( f(x) \) è la funzione esterna. La funzione interna che introdurremo, ovvero \( g(u) \), sarà una funzione a nostra scelta ma tale da poter essere invertibile. Infatti, una volta calcolato l’integrale a secondo membro rispetto alla variabile \( u \), dovremo effettuare la sostituzione \( u=g^{-1}(x) \) in modo da poter esprimere il risultato finale dell’integrale in funzione della variabile \( x \).
Inoltre, dovremo chiaramente scegliere \( g(x) \) di modo che l’integrale diventi più semplice da calcolare, effettuando fin da subito la sostituzione \( x = g(u) \).
Vista la forma del primo membro l’utilità della formula è chiara: poter integrare un’espressione che non si presenta come un prodotto tra una funzione composta e la derivata del suo argomento. Abbiamo così una seconda formula di integrazione per sostituzione che ci permette di cavarcela nei casi ove la prima formula non risulta utile.
Esempi
Esempio 1
Calcolare:
\[ \int \log x \, dx \]
Riconduciamo la funzione da integrare ad una funzione composta. Poiché si ha che \( \log_e e^x = x \), appare qui conveniente utilizzare come funzione interna \( g(u)=e^u \). In tal modo ci ritroveremo a calcolare, come vedremo, un integrale più semplice. Inoltre la funzione \( e^x \) è invertibile e la sua inversa è proprio \( \log x \).
Attenzione: il logaritmo ha come dominio i soli reali positivi e di conseguenza dovremo restringere il dominio di \( e^x \) ai soli reali positivi, di modo che questa sia invertibile.
Dovremo quindi effettuare subito la sostituzione \( x = g(u)=e^u \), calcolare l’integrale indefinito rispetto ad \( u \) ed infine eseguire la sostituzione con la funzione inversa \( u=g^{-1} (x) \), ovvero \( u = \log x \).
Tenendo conto di tutto quanto detto, applicando la formula di integrazione per sostituzione della seconda specie abbiamo:
\[ \begin{align}&{\int \log x \, dx = \left\{\int \left[\log(e^u)\cdot \dfrac{d}{du}(e^u) \right] \, du \right\}_{u=\log x}}= \\ \\ & =\left[\int u \cdot e^u \, du \right]_{u=\log x } \end{align} \]
L’integrale \( \displaystyle \int u \cdot e^u \, du \) deve essere calcolato con la formula di integrazione per parti. Si ha:
\[ \displaystyle \int u \cdot e^u \, du=u \cdot e^u – \int 1\cdot e^u \, du=u\cdot e^u – e^u+c = e^u(u-1)+c= \]
Sostituendo alla \( u \) l’espressione \( \log x \) si ha in conclusione:
\[ = \left[e^u(u-1)+c \right]_{u = \log x}=x(\log x-1)+c, \quad c \in \mathbb{R} \]
Abbiamo così calcolato l’integrale indefinito della funzione logaritmo, mostrando una strada alternativa al solo utilizzo della formula di integrazione per parti. Con il metodo qui utilizzato non abbiamo avuto bisogno di riguardare la funzione logaritmo come \( \log x \cdot 1 \).
Esempio 2
Calcolare:
\[ \int \dfrac{e^x+1}{e^x} \, dx \]
Qui ci ritroviamo ad integrare una funzione che è composta. Tuttavia, dobbiamo ancora applicare la seconda formula di integrazione per sostituzione poiché nell’espressione da integrare non compare un fattore dato dalla derivata dell’argomento della funzione composta.
Scegliamo:
\[ g(u)= \log u\]
Dovremo così porre fin da subito la sostituzione \( x = \log u \). Dopo aver calcolato l’integrale indefinito rispetto ad \( u \) concluderemo l’esercizio sostituendo la funzione inversa \( u = e^x \).
Si ha:
\[ \begin{align}&\int \dfrac{e^x+1}{e^x} \, dx= \left[ \int \dfrac{e^{\log u}+1}{e^{\log u}} \cdot \dfrac{d}{du}\log u \, du\right]_{u = e^x} = \left[\int \dfrac{u+1}{u} \cdot \dfrac{1}{u} \, du\right]_{u=e^x}= \\ \\ & = \left[\int \dfrac{u+1}{u^2} \, du\right]_{u=e^x}=\left[\int \dfrac{1}{u}+ \dfrac{1}{u^2} \, du \right]_{u=e^x}= \left[\log |u|+ \int u^{-2} \, du \right]_{u=e^x} = \\ \\ & = \left[\log |u|+\dfrac{1}{-1\cdot u}+c \right]_{u=e^x} = \log e^x -\dfrac{1}{e^x}+c = x-\dfrac{1}{e^x}+c, \quad c \in \mathbb{R} \end{align} \]
Esempio 3
Attenzione: questo esempio è destinato più che altro agli studenti universitari. L’esempio mostra varie tecniche ed è una buona occasione per cominciare a vedere come si integrano le funzioni razionali. Ci occuperemo dettagliatamente del problema dell’integrazione delle funzioni razionali nelle prossime lezioni. I casi presenti nell’esempio a seguire sono tra i più semplici.
Calcolare:
\[ \int \dfrac{\log \left(\sqrt[3]{x} -1\right)}{\sqrt{x}}\, d x \]
Anche in questo caso non possiamo applicare la prima formula di integrazione per sostituzione poiché non abbiamo come fattore la derivata della funzione più interna.
Utilizziamo allora la seconda formula scegliendo ad esempio la funzione invertibile \( g(u)=u^6 \). L’idea di questa scelta è quella di fare sparire le radici nell’integrale in \( u \). 😉
Dovremo così porre subito la sostituzione \( x = u^6 \), calcolare l’integrale nella variabile \( u \) e in conclusione sostituire con la funzione inversa, ovvero porre la sostituzione \( u = \sqrt[6]{x} \).
Applicando la formula abbiamo:
\[ \begin{align}&\int \dfrac{\log \left(\sqrt[3]{x} -1 \right)}{\sqrt{x}} \, dx = \left\{\int \left[\dfrac{\log(\sqrt[3]{u^6}-1)}{\sqrt{u^6}}\cdot 6u^5 \right] \, du \right\}_{u=\sqrt[6]{x}}= \\ \\ & = \left\{\int \left[\dfrac{\log\left(u^2-1 \right)}{u^3} \cdot 6u^5 \, \right]du\right\}_{u=\sqrt[6]{x}} = \left\{6\int \left[\log(u^2-1) \cdot u^2 \right] \, du \right\}_{u=\sqrt[6]{x}}\end{align} \]
Ci ritroviamo con un integrale da calcolare per parti:
\[ 6\int \left[\log(u^2-1) \cdot u^2 \right] \, du \]
Conviene porre \( f(x)=\log(u^2-1) \) e \( h(x) = u^2 \). Infatti risulterebbe piuttosto scomodo integrare la funzione \( \log(u^2-1) \) mentre è abbastanza agevole derivarla (basta utilizzare la regola della derivata della funzione composta). Inoltre non abbiamo problemi a ricavare un’antiderivata per \( h(x) = u^2 \). Con le scelte fatte, applicando la formula dell’integrazione per parti si ha:
\[ \begin{align}&6\int \left[\log(u^2-1) \cdot u^2 \right] \, du=6\cdot \left[\log (u^2-1)\cdot \dfrac{u^3}{3}- \int \dfrac{1}{u^2-1} \cdot 2u\cdot \dfrac{u^3}{3} \, du \right]= \\ \\\ & = 6 \cdot \left[\dfrac{u^3 \log (u^2-1)}{3} – \dfrac{1}{3}\int \dfrac{2u^4}{u^2-1} \, du\right] =\dfrac{6}{3}\cdot \left[u^3 \log (u^2-1)-2 \int \dfrac{u^4}{u^2-1} \, du \right] = \\ \\ & = 2 u^3 \log (u^2-1)-4\int \dfrac{u^4}{u^2-1} \, du = (*) \end{align} \]
L’integrale \( \displaystyle 4\int \dfrac{u^4}{u^2-1} \, du \) è un esempio di integrale di funzione razionale. In questo caso è sufficiente utilizzare la divisione tra polinomi e quindi la regola dell’integrale della somma di funzioni.
Eseguiamo la divisione tra polinomi in modo da poter riesprimere la frazione algebrica \( \dfrac{u^4}{u^2-1} \) in una forma più facile da integrare:
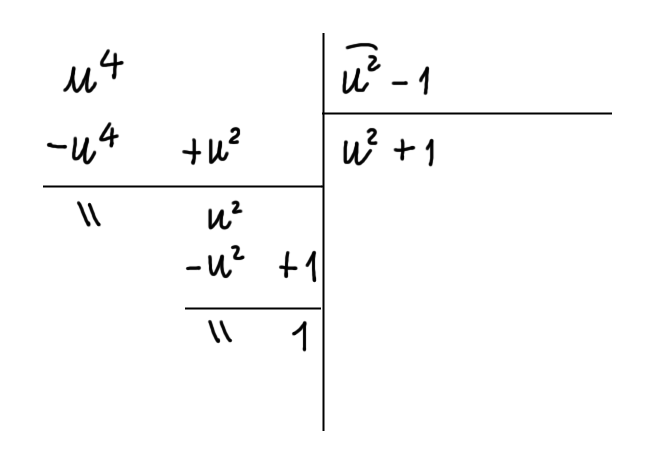
Per quanto sappiamo sulla divisione tra polinomi possiamo scrivere:
\[ \dfrac{u^4}{u^2-1}=\dfrac{1}{u^2-1}+u^2+1 \]
E quindi per l’integrale:
\[ \begin{align}&4\int \dfrac{u^4}{u^2-1} \, du=4 \int\left[\dfrac{1}{u^2-1}+u^2+1 \right] \, du = \\ \\ & = 4 \left[\int \dfrac{1}{u^2-1}\, du + \int u^2 \, du + \int 1 \, du \right]= \\ \\ & \end{align} \]
Un’altra difficoltà è data dall’integrale corrispondente al primo termine entro le parentesi quadre, ovvero:
\[ \int \dfrac{1}{u^2-1}\, du \]
Osserviamo che si ha:
\[ \dfrac{1}{u^2-1} = \dfrac{1}{(u-1)(u+1)} \]
L’idea è quella di esprimere la quantità da integrare come differenza tra due frazioni algebriche aventi ancora numeratore \( 1 \) e aventi per denominatore uno dei fattori utilizzati per la scomposizione del denominatore. Scegliamo la differenza proprio nella speranza che sommando le due frazioni al numeratore la variabile \( u \) sparisca. Intanto abbiamo:
\[ \dfrac{1}{u-1}-\dfrac{1}{u+1}=\dfrac{u+1-u+1}{(u-1)(u+1)}=\dfrac{2}{(u-1)(u+1)} \]
ma allora:
\[ \dfrac{1}{u^2-1} = \dfrac{1}{2} \left(\dfrac{1}{u-1}-\dfrac{1}{u+1} \right) \]
e quindi possiamo calcolare il precedente integrale:
\[ \begin{align}&4 \left[\int \dfrac{1}{u^2-1}\, du + \int u^2 \, du + \int 1 \, du \right]= \\ \\ & = 4 \left[\int \dfrac{1}{2}\left(\dfrac{1}{u-1}-\dfrac{1}{u+1} \right)+\int u^2 \, du + \int 1 \, du \right] = \\ \\ & = 4 \left[\dfrac{1}{2} \left(\log |u-1|-\log |u+1|\right)+\dfrac{u^3}{3}+u+c \right]\end{align} \]
Osserviamo che ad esempio l’integrale \( \displaystyle \int \dfrac{1}{u-1}\, du \) è stato calcolato utilizzando la prima formula di sostituzione. Infatti, in questo caso abbiamo seppur nascosto come fattore la derivata dell’argomento, poiché questa è 1. 😉
Riprendendo i precedenti passaggi, per tutto quanto visto abbiamo:
\[ \begin{align}& (*) = 2 u^3 \log (u^2-1)-4 \left[\dfrac{1}{2} \left(\log |u-1|-\log |u+1|\right)+\dfrac{u^3}{3}+u \right]= \\ \\ & = 2u^3\log (u^2-1)-2 \left(\log|u-1| -\log|u+1|\right)-\dfrac{4}{3}u^3-4u= \\ \\ & = 2u^3 \log(u^2-1)-2\log \left|\dfrac{u-1}{u+1} \right|-\dfrac{4}{3}u^3 -4 u \end{align} \]
Per concludere non dimentichiamo la sostituzione finale. Dobbiamo in particolare porre \( u = \sqrt[6]{x} \). Otteniamo così:
\[ \begin{align}&\left[2u^3 \log(u^2-1)-2\log \left|\dfrac{u-1}{u+1} \right|-\dfrac{4}{3}u^3 -4 u +c \right]_{u=\sqrt[6]{x}}= \\ \\ & = 2(\sqrt[6]{x})^3 \log[(\sqrt[6]{x})^2-1]-2\log\left| \dfrac{\sqrt[6]{x}-1}{\sqrt[6]{x}+1}\right|-\dfrac{4}{3}(\sqrt[6]{x})^3-4 \sqrt[6]{x}+c= \\ \\ & = 2 \sqrt{x}\log (\sqrt[3]{x}-1)-2\log \left|\dfrac{\sqrt[6]{x}-1}{\sqrt[6]{x}+1}\right| -\dfrac{4}{3}\sqrt{x}-4 \sqrt[6]{x}+c \end{align} \]
Integrali definiti per sostituzione
Per chi già conosce gli integrali definiti è disponibile la lezione: integrali definiti per sostituzione.
Per quanto riguarda la tecnica di integrazione per sostituzione è tutto. Chi già conosceva un po’ l’argomento avrà notato che in questa lezione non abbiamo utilizzato il concetto di differenziale. Ciò è voluto poiché preferiamo in una prima fase ragionare esclusivamente secondo le conseguenze del teorema della derivata della funzione composta.
Se comunque volete utilizzare sin d’ora il concetto di differenziale per la risoluzione degli integrali per sostituzione è disponibile la lezione: integrazione per sostituzione e differenziale. Diversamente, potete continuare a seguire le lezioni nel loro ordine. Il differenziale verrà comunque introdotto tra poche lezioni. 😉
Nella prossima lezione ci occuperemo delle sostituzioni con esponenziali e logaritmi negli integrali. Buon proseguimento con Altramatica! 🙂
