Distanza tra due rette nello spazio

La distanza tra due rette nello spazio nel caso di rette sghembe è data dalla più piccola tra tutte le possibili distanze tra due punti appartenenti rispettivamente alla prima e alla seconda retta. Nel caso di rette incidenti e di rette parallele coincidenti la distanza tra le due rette è nulla. Infine, nel caso di rette parallele distinte, la loro distanza si riduce alla distanza tra un qualsiasi punto della prima retta e la seconda retta (distanza tra un punto e una retta nello spazio).

In questa lezione mostreremo come calcolare la distanza tra due rette nello spazio, distinguendo tra i vari casi possibili. Ci occuperemo in particolare del caso di due rette nello spazio sghembe, poiché negli altri casi il calcolo della distanza tra le due rette è banale o comunque è riconducibile al caso del calcolo della distanza tra un punto e una retta nello spazio, che abbiamo visto nella precedente lezione.

Prima di introdurre e dimostrare il teorema per il calcolo della distanza tra due rette non parallele, è tuttavia opportuno richiamare le definizioni di rette incidenti, rette parallele distinte, rette parallele coincidenti e rette sghembe, in modo da poter analizzare i vari casi.

Possibili casi che si possono incontrare nel calcolo della distanza tra due rette

Rette incidenti

Due rette nello spazio si dicono incidenti se sono non parallele tra loro ed esiste un piano in grado di contenerle entrambe. Più semplicemente, due rette si dicono incidenti se hanno un punto in comune, detto punto di intersezione.

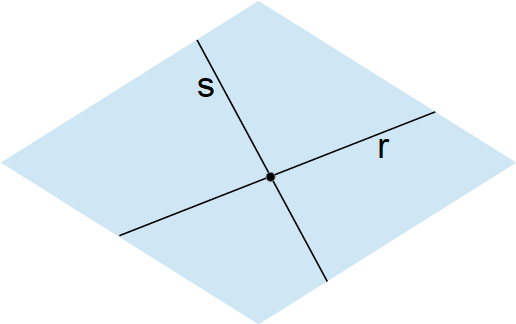
Le due rette ${r}$ ed ${s}$ sono incidenti ed infatti hanno un punto di intersezione.

Nel caso di rette incidenti, la loro distanza è nulla.

Rette parallele coincidenti

Due rette parallele sono coincidenti se hanno tutti i punti in comune.

Anche in questo caso, la distanza tra le due rette è nulla.

Rette parallele e distinte

Due rette nello spazio sono parallele e distinte se esiste un piano in grado di contenerle entrambe e non hanno nessun punto in comune.

In questo caso, basta prendere un qualsiasi punto appartenente ad esempio alla retta ${s}$ . La distanza tra le due rette sarà data dalla distanza tra il punto scelto della retta ${s}$ e la retta ${r}$ . Ci riconduciamo in questo modo al caso della distanza tra un punto e una retta nello spazio.

Esempio (calcolo della distanza tra due rette parallele e distinte)

Calcolare la distanza tra la retta ${r}$ passante per il punto ${P_0=(1,2,3)}$ e la retta ${s}$ passante per il punto ${P_1=(4,5,6)}$ , entrambe parallele al vettore ${\textbf{m}=\left \langle {-1,2,5} \right \rangle}$ .

Il problema proposto equivale ad esempio a dover calcolare la distanza tra il punto ${P_0}$ e la retta ${s}$ . In alternativa, sarebbe del tutto equivalente calcolare la distanza tra il punto ${P_1}$ e la retta ${r}$ .

Ricordiamo la formula per il calcolo della distanza tra un punto e una retta:

d=\dfrac{|\overrightarrow{P_0P_1} \times \textbf{n}|}{\lVert {\textbf{n}} \rVert}

Abbiamo:

\begin{align*} & \overrightarrow{P_0P_1}=\left \langle {x_1-x_0, y_1-y_0, z_1-z_0} \right \rangle=\left \langle {4-1, 5-2, 6-3} \right \rangle= \\ \\ & =\left \langle {3,3,3} \right \rangle \end{align*}

Calcoliamo ora il vettore ${\textbf{n}}$ :

\textbf{n}=\textbf{m} \land (\textbf{m } \land \overrightarrow{P_0P_1})

Cominciamo dal prodotto vettoriale all’interno delle parentesi tonde:

\begin{align*} & \textbf{m } \land \overrightarrow{P_0P_1}=\det \begin{pmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ -1 & 2 & 5\\ 3 & 3 & 3\end{pmatrix}= \\ \\ & =\textbf{i}(2 \cdot 3 - 3 \cdot 5)-\textbf{j}(-1 \cdot 3 - 3 \cdot 5 )+\textbf{k}(-1 \cdot 3 - 3 \cdot 2)=\\ \\ & =-9\textbf{i}+18\textbf{j}-9\textbf{k} \end{align*}

e quindi:

\small \begin{align*} &\textbf{n}=\textbf{m} \land (\textbf{m } \land \overrightarrow{P_0P_1}) =\det\begin{pmatrix} \textbf{i} & \textbf{j } & \textbf{k} \\ -1 & 2 & 5 \\ -9 & 18 & -9\end{pmatrix}=\\ \\ & =\textbf{i}[2 \cdot (-9)-18 \cdot 5]-\textbf{j}[-1 \cdot (-9)-(-9)\cdot5]+\textbf{k}[-1 \cdot 18]-(-9)\cdot 2]=\\ \\ & =(-18-90)\textbf{i}-(9+45)\textbf{j}+0\cdot\textbf{k}=-108\textbf{i}-54\textbf{j}\end{align*}

Ora possiamo calcolare la distanza cercata:

\begin{align*} &d=\dfrac{|\overrightarrow{P_0P_1} \times \textbf{n}|}{\lVert {\textbf{n}} \rVert} = \dfrac{|\left \langle {3,3,3} \right \rangle \times \left \langle {-108,-54,0} \right \rangle|}{\sqrt{(-108)^2+(-54)^2+0}}=\\ \\ & =\dfrac{|3 \cdot (-108)+3 \cdot (-54)+0|}{\sqrt{11664+2916}}=\dfrac{|-324-162|}{\sqrt{14580}}=\\ \\ & =\dfrac{|-486|}{\sqrt{14580}}\approx 4,02\end{align*}

Calcolo della distanza tra due rette sghembe

Eccoci arrivati all’ultimo caso, relativo al calcolo della distanza tra due rette sghembe.

Due rette nello spazio si dicono sghembe se non sono parallele tra loro e se non esiste alcun piano in grado di contenerle entrambe.

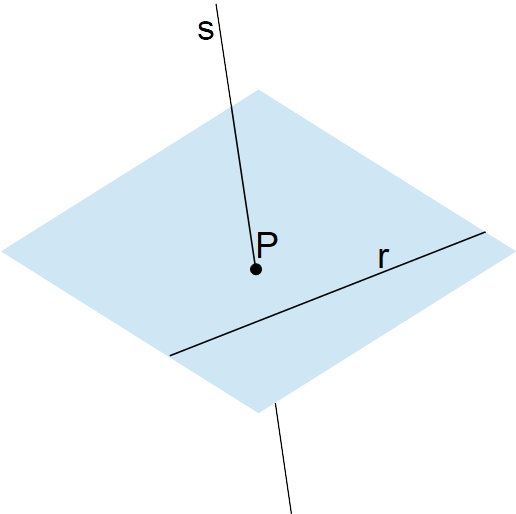
Per il calcolo della distanza tra due rette sghembe utilizzeremo il seguente teorema, relativo alla distanza tra due rette non parallele.

Come calcolare la distanza tra due rette non parallele (teorema)

Teorema (distanza tra due rette non parallele). Sia dato un punto ${P_1=(x_1, y_1, z_1)}$ appartenente alla retta ${r_1}$ parallela al vettore ${\textbf{m}_1}$ . Sia inoltre dato un punto ${P_2=(x_2, y_2, z_2)}$ appartenente alla retta ${r_2}$ parallela al vettore ${\textbf{m}_2}$ . I due vettori ${\textbf{m}_1}$ e ${\textbf{m}_2}$ siano tra loro non paralleli (di conseguenza, le due rette non sono tra loro parallele). Inoltre, sia ${\textbf{n}=\textbf{m}_1 \land \textbf{m}_2}$ .

Sotto tali ipotesi, la distanza tra le rette ${r_1}$ e ${r_2}$ è data dalla lunghezza della proiezione del vettore ${\overrightarrow{P_1P_2}}$ lungo la direzione del vettore ${\textbf{n}}$ . In particolare si ha:
${d=\lVert {\textbf{P}_{\textbf{n}}(\overrightarrow{P_1P_2})} \rVert=\dfrac{|\overrightarrow{P_1P_2} \times \textbf{n}|}{\lVert {\textbf{n}} \rVert}}$

Dimostrazione

Cominciamo osservando che esistono necessariamente due punti ${R_1}$ ed ${R_2}$ , appartenenti rispettivamente alla retta ${r_1}$ e alla retta ${r_2}$ , tali che la loro distanza ${\lVert {\overrightarrow{R_1R_2}} \rVert}$ sia la minima fra tutte le possibili distanze tra due generici punti rispettivamente della retta ${r_1}$ e della retta ${r_2}$ .

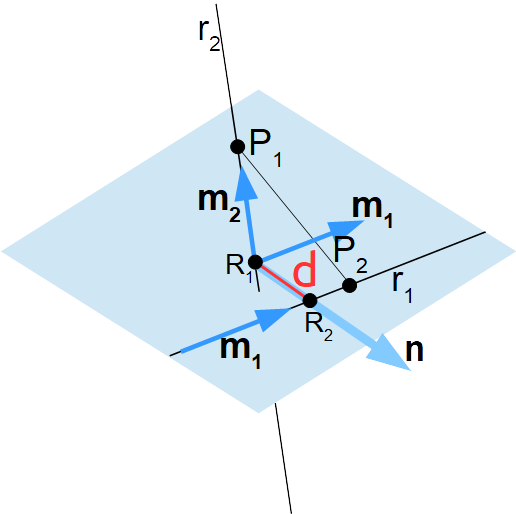
Ora, il vettore ${\overrightarrow{R_1R_2}}$ è perpendicolare ad entrambe le rette. Ma allora, il vettore ${\textbf{n}}$ , che per le proprietà del prodotto vettoriale è perpendicolare sia a ${\textbf{m}_1}$ , sia ad ${\textbf{m}_2}$ , e quindi ad entrambe le rette, è necessariamente parallelo al vettore ${\overrightarrow{R_1R_2}}$ . Ed in particolare, ${\lVert {\overrightarrow{R_1R_2}} \rVert}$ è la lunghezza della proiezione del vettore ${\overrightarrow{P_1P_2}}$ lungo la direzione di ${\textbf{n}}$ :

\lVert {\overrightarrow{R_1R_2}} \rVert=\lVert {\textbf{P}_{\textbf{n}}(\overrightarrow{P_1P_2})} \rVert

Ma per quanto sappiamo sulle proiezioni di vettori:

\lVert {\textbf{P}_{\textbf{n}}(\overrightarrow{P_1P_2})} \rVert=\dfrac{|\overrightarrow{P_1P_2} \times \textbf{n}|}{\lVert {\textbf{n}} \rVert}

e quindi in conclusione, per la distanza cercata ${d}$ :

d=\lVert {\overrightarrow{R_1R_2}} \rVert=\dfrac{|\overrightarrow{P_1P_2} \times \textbf{n}|}{\lVert {\textbf{n}} \rVert}

Il teorema è così dimostrato.

Dunque, per calcolare la distanza tra due rette non parallele basta conoscere un punto appartenente alla prima retta, un punto appartenente alla seconda retta, un vettore parallelo alla prima retta e un vettore parallelo alla seconda retta. Il vettore ${\overrightarrow{n}}$ presente nella formula è dato dal prodotto vettoriale tra i due vettori paralleli alle rette. Il vettore ${\overrightarrow{P_1P_2}}$ si calcola agevolmente a partire dalle coordinate dei punti ${P_1}$ e ${P_2}$ .

Osserviamo che il teorema è valido sia per rette tra loro sghembe, sia per rette tra loro incidenti. Nel secondo caso, infatti, il vettore ${\overrightarrow{P_1P_2}}$ è necessariamente complanare ai vettori ${\textbf{m}_1}$ e ${\textbf{m}_2}$ . Di conseguenza, i vettori ${\overrightarrow{P_1P_2}}$ e ${\textbf{n}}$ sono tra loro perpendicolari, e pertanto il loro prodotto scalare è nullo. Quindi, per la formula del teorema appena dimostrato la distanza tra due rette incidenti è nulla. Ritroviamo così conferma di quanto detto all’inizio della lezione a proposito della distanza fra rette incidenti.

Vediamo a questo punto un esempio sul calcolo della distanza tra due rette sghembe.

Esempio (calcolo della distanza tra due rette sghembe)

Calcolare la distanza tra la retta ${r_1}$ avente equazione cartesiana: ${\small \dfrac{2x-4}{5}=\dfrac{y-9}{4}=\dfrac{3z-9}{2}}$ e la retta ${r_2}$ avente equazione cartesiana: $\small {\dfrac{x+1}{2}=\dfrac{y+3}{4}=\dfrac{z+6}{5}}$

Il problema sta anzitutto nell’individuare per ciascuna retta un punto ad essa appartenente ed un vettore ad essa parallelo. Ma tale problema è di immediata risoluzione ricordando la forma generale delle equazioni cartesiane di una retta nello spazio:

\dfrac{x-x_0}{a}=\dfrac{y-y_0}{b}=\dfrac{z-z_0}{c}

relativa ad una retta alla quale appartiene il punto ${P_0=(x_0, y_0, z_0)}$ e parallela al vettore ${\textbf{m}=\left \langle {a,b,c} \right \rangle}$ .

Si tratterà allora di riscrivere le equazioni cartesiane relativa a ciascuna retta in questa precisa forma, in modo da ricavare per ogni retta un punto ad essa appartenente e un vettore ad essa parallela.

Cominciamo dalle equazioni cartesiane relative alla prima retta:

\dfrac{2x-4}{5}=\dfrac{y-9}{4}=\dfrac{3z-9}{2}

che riscritte nella forma generale divengono:

\dfrac{\frac{2x-4}{2}}{\frac{5}{2}}=\dfrac{y-9}{4}=\dfrac{\frac{3z-9}{3}}{\frac{2}{3}}

e quindi:

\dfrac{x-2}{5/2}=\dfrac{y-9}{4}=\dfrac{z-3}{2/3}

Otteniamo quindi per la prima retta, ovvero la retta ${r_1}$ :

P_1=(2,9,3), \qquad \textbf{m}_1=\left \langle {5/2, \: 4, \: 2/3} \right \rangle

Procediamo allo stesso modo con le equazioni cartesiane relative alla seconda retta, ovvero la retta ${r_2}$ :

\dfrac{x+1}{2}=\dfrac{y+3}{4}=\dfrac{z+6}{5}

Riscriviamo le equazioni nella seguente forma:

\dfrac{x-(-1)}{2}=\dfrac{y-(-3)}{4}=\dfrac{z-(-6)}{5}

Otteniamo per la retta ${r_2}$ le seguenti informazioni:

P_2=(-1, -3, -6), \qquad \textbf{m}_2=\left \langle {2,4,5} \right \rangle

Ora disponiamo di tutti i dati per poter calcolare la distanza tra le due rette.

Cominciamo calcolando il vettore ${\textbf{n}}$ :

\small \begin{align*} & \textbf{n}=\textbf{m}_1 \land \textbf{m}_2=\det \begin{pmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ 5/2 & 4 & 2/3 \\ 2 & 4 & 5 \end{pmatrix}= \\ \\ & =\textbf{i}(4 \cdot 5-4 \cdot 2/3)-\textbf{j}(5/2 \cdot 5 - 2 \cdot 2/3)+\textbf{k}(5/2 \cdot 4 -2 \cdot 4)=\\ \\ & =\dfrac{52}{3}\textbf{i}-\dfrac{67}{6}\textbf{j}+2\textbf{k}=\left \langle {\dfrac{52}{3}, -\dfrac{67}{6}, 2} \right \rangle\end{align*}

Calcoliamo il vettore ${\overrightarrow{P_1P_2}}$ :

\overrightarrow{P_1P_2}=\left \langle {-1-2, -3-9,-6-3} \right \rangle=\left \langle {-3,-12,-9} \right \rangle

Abbiamo così:

\begin{align*} & d=\dfrac{|\overrightarrow{P_1P_2} \times \textbf{n}|}{\lVert {\textbf{n}} \rVert}= \dfrac{\left|\left \langle {-3,-12,-9} \right \rangle \times \left \langle {\dfrac{52}{3}, -\dfrac{67}{6}, 2} \right \rangle \right|}{\sqrt{\left( \dfrac{52}{3}\right)^2+\left( -\dfrac{67}{6}\right)^2+\left( -2\right)^2}}= \\ \\ & =\dfrac{\left|3 \cdot \left \langle {-1, -4, -3} \right \rangle \times \left \langle {\dfrac{52}{3}, -\dfrac{67}{6}, 2} \right \rangle \right|}{\sqrt{\dfrac{2704}{9}+\dfrac{4489}{36}+4}}=\\ \\ & \approx \dfrac{\left|3 \cdot \left[ -1 \cdot \dfrac{52}{3}+(-4) \cdot \left( -\dfrac{67}{6}\right)-3 \cdot 2\right]\right|}{20,71566}=\\ \\ & =\dfrac{\left|3\cdot \left( -\dfrac{52}{3}+\dfrac{134}{3}-\dfrac{18}{3}\right)\right|}{20,71566}=\\ \\ & =\dfrac{3 \cdot \dfrac{64}{3} }{20,71566}=\dfrac{64}{20,71566} \approx 3,09 \end{align*}

Conclusioni

Per quanto riguarda questa lezione sul calcolo della distanza tra due rette nello spazio è tutto. Qui si concludono le lezioni relative ai vettori e alla geometria con i vettori (geometria vettoriale) di Altramatica. Buono studio a tutti voi!