Distanza tra un punto e una retta nello spazio

 - 

Vettori (università)

La distanza tra un punto P₀ e una retta r nello spazio è per definizione la lunghezza della proiezione su un vettore normale alla retta r della distanza tra il punto P₀ e un qualsiasi punto P₁ appartenente alla retta r.

Detta così, probabilmente la definizione di distanza tra un punto {P} e una retta {r} nello spazio appare un po’ oscura. Tuttavia, nel corso della lezione chiariremo tutti i concetti necessari per comprendere al meglio questa definizione. Ed in particolare, richiameremo le nozioni relative alla proiezione di vettori, argomento del quale ci siamo occupati nel dettaglio nella lezione del link.

Una volta introdotta la definizione di distanza tra un punto e una retta nello spazio, forniremo la dimostrazione della corrispondente formula e svolgeremo insieme un esercizio di esempio.

Precisiamo che qui ci occupiamo della nozione di distanza tra un punto e una retta dello spazio vista a livello universitario.

Definizione di distanza tra un punto e una retta nello spazio

Teorema (formula della distanza tra un punto e una retta nello spazio). Sia {P=(x_0, y_0, z_0)} un punto dello spazio tridimensionale. Sia inoltre {r} una retta dello spazio parallela ad un certo vettore {\textbf{m}}. Inoltre, sia {P_1=(x_1, y_1, z_1)} un punto qualsiasi della retta {r}. Consideriamo altresì un vettore {\textbf{n}} dato da {\textbf{n}= \textbf{m} \land (\textbf{m} \land \overrightarrow{P_0P_1})}.
Sotto tali ipotesi, la distanza tra il punto {P_0} e la retta {r} è data dalla lunghezza della proiezione ortogonale di {\overrightarrow{P_0P_1}} lungo la direzione di {\textbf{n}}. In altre parole, la distanza tra {P_0} e {r} è data da:{\dfrac{|\overrightarrow{P_0P_1}\times \textbf{n}|}{\lVert {\textbf{n}} \rVert}}

Dimostrazione

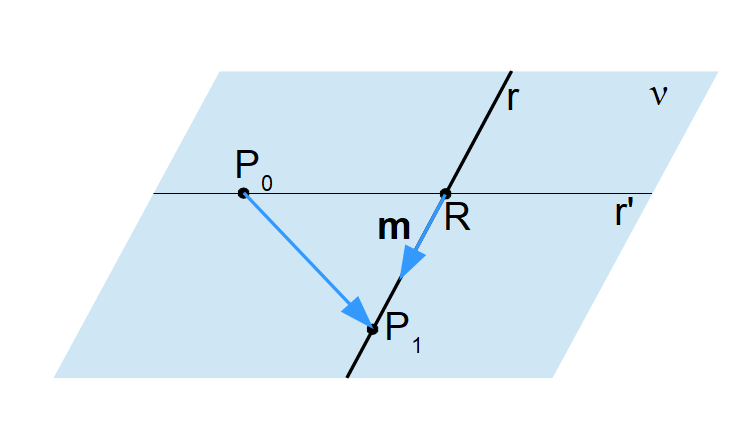
Per chiarire intanto la definizione, vediamo di aiutarci con la seguente figura:

Il nostro obiettivo è calcolare la distanza tra il punto {P_0=(x_0, y_0, z_0)} e la retta {r} giacente sul piano {\nu}. E per definizione, tale distanza è valutata lungo la direzione della retta {r'}, che è la retta normale ad {r}, anch’essa giacente sul piano {\nu}, e passante per il punto {P_0}.

Il punto {P_1=(x_1, y_1, z_1)} è un punto scelto a piacere appartenente alla retta {r}.

Il punto {R} è dato dall’intersezione delle rette {r} e {r'}.

Così, la distanza tra il punto {P_0} e la retta {r} è data, per tutto quanto detto, dalla lunghezza del vettore {\overrightarrow{P_0R}}, ovvero {\lVert {\overrightarrow{P_0R}} \rVert}.

Consideriamo ora il vettore {\overrightarrow{P_0P_1}} e un vettore {\textbf{m}} parallelo alla retta {r}.

Cerchiamo ora di comprendere le proprietà del vettore:

\textbf{n}=\textbf{m} \land (\textbf{m} \land \overrightarrow{P_0P_1})

Intanto, cominciamo con il rappresentare in figura il vettore {\textbf{m} \land \overrightarrow{P_0P_1}}. Per fare ciò, conviene per comodità applicare il vettore {\overrightarrow{P_0P_1}} al punto {R}:

Adesso, se consideriamo il prodotto vettoriale {\textbf{m} \land (\textbf{m} \land \overrightarrow{P_0P_1})} otteniamo il vettore {\textbf{n}} come in figura:

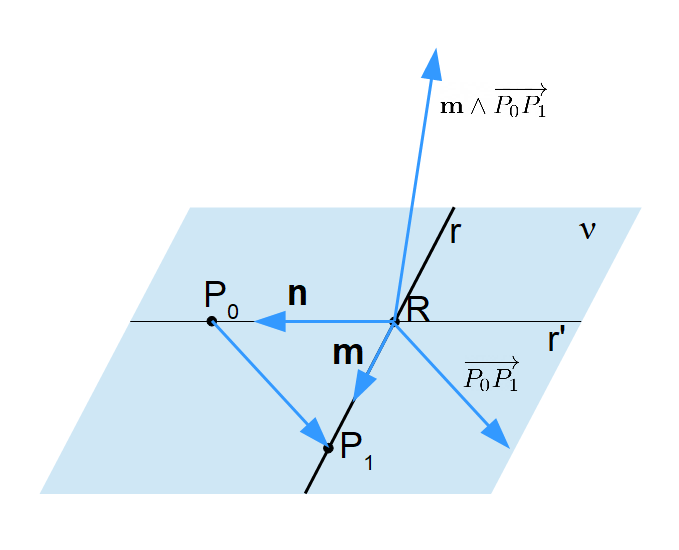
Si tratta ora di dimostrare che il vettore {\textbf{n}} è parallelo a {\overrightarrow{P_0R}}. E ciò equivale a dimostrare che {\textbf{n}} sia perpendicolare alla retta {r} e sia giacente sul piano {\nu}.

Ora, poiché {\textbf{n}=\textbf{m} \land (\textbf{m} \land \overrightarrow{P_0P_1})}, abbiamo che {\textbf{n}} dovrà essere perpendicolare sia a {\textbf{m}}, sia a {\textbf{m} \land \overrightarrow{P_0P_1}}.

Se {\textbf{n}} è perpendicolare a {\textbf{m}}, allora {\textbf{n}} è anche perpendicolare a {r}.

Inoltre, dato che i vettori {\textbf{m}} e {\overrightarrow{P_0P_1}} sono tra loro non pararelli, sicuramente il vettore {\textbf{m} \land \overrightarrow{P_0P_1}} è normale al piano ove giacciono entrambi i vettori {\textbf{m}} e {\overrightarrow{P_0P_1}}. Quindi il vettore {\textbf{m} \land \overrightarrow{P_0P_1}} è normale al piano {\nu}. Ma allora il vettore {\textbf{n}=\textbf{m} \land (\textbf{m} \land \overrightarrow{P_0P_1})}, che per le proprietà del prodotto vettoriale è perpendicolare al vettore {\textbf{m} \land \overrightarrow{P_0P_1}}, è necessariamente giacente sul piano {\nu}.

Abbiamo così dimostrato che il vettore {\textbf{n}} è parallelo al vettore {\overrightarrow{P_0R}}.

Ma a questo punto, basta osservare che il vettore {\overrightarrow{P_0R}} è la proiezione ortogonale del vettore {\overrightarrow{P_0P_1}} su {\textbf{n}}, e quindi per la sua lunghezza abbiamo:

\lVert {\overrightarrow{P_0R}} \rVert=\lVert {\textbf{P}_{\textbf{n}}(\overrightarrow{P_0P_1})} \rVert

e per quanto sappiamo sulle proiezioni di vettori:

\lVert {\textbf{P}_{\textbf{n}} (\overrightarrow{P_0P_1})} \rVert=\dfrac{|\overrightarrow{P_0P_1} \times\textbf{n}|}{\lVert {\textbf{n}} \rVert}

e quindi:

\lVert {\overrightarrow{P_0R}} \rVert=\dfrac{|\overrightarrow{P_0P_1} \times\textbf{n}|}{\lVert {\textbf{n}} \rVert}

Il teorema relativo alla formula della distanza tra un punto e una retta nello spazio è così dimostrato.

Esempio (come calcolare la distanza tra un punto e una retta nello spazio)

Calcolare la distanza tra il punto {P_0=(x_0, y_0, z_0)=(5,3,3)} e la retta {r} avente equazioni cartesiane {x-1=\dfrac{y+8}{-4}=\dfrac{z-7}{3}}.

Riscriviamo anzitutto le equazioni cartesiane della retta data nella forma:

\dfrac{x-x_1}{a}=\dfrac{y-y_1}{b}=\dfrac{z-z_1}{c}

Abbiamo nel nostro caso:

\dfrac{x-1}{1}=\dfrac{y-(-8)}{-4}=\dfrac{z-7}{3}

da cui:

x_1= 1, \: y_1 = -8, \: z_1=7, \qquad a=1, \: b=-4, \: c=3

Di conseguenza, il punto {P_1=(x_1, y_1, z_1)=(1,-8,7)} appartiene alla retta {r} e il vettore {\textbf{m}=\left \langle {1, -4, 3} \right \rangle} è parallelo alla retta stessa.

Cominciamo calcolando il vettore {\textbf{n}}:

\textbf{n}=\textbf{m} \land (\textbf{m} \land \overrightarrow{P_0P_1})

Essendo noti entrambi i punti {P_0} e {P_1} abbiamo intanto:

\begin{align*} & \overrightarrow{P_0P_1}=\left \langle {x_1-x_0, y_1-y_0, z_1-z_0} \right \rangle= \\ \\ & =\left \langle {1-5, -8-3, 7-3} \right \rangle= \left \langle {-4, -11, 4} \right \rangle \end{align*}

Iniziamo dal prodotto vettoriale all’interno delle parentesi tonde:

\small \begin{align*} &\textbf{m} \land \overrightarrow{P_0P_1}= \left \langle {1,-4,3} \right \rangle \times \left \langle {-4, -11, 4} \right \rangle= \\ \\ & =\det \begin{pmatrix} \textbf{i } & \textbf{j} & \textbf{k} \\ 1 & -4 & 3 \\ -4 & -11 & 4\end{pmatrix}=\\ \\ & =\textbf{i}\det \begin{pmatrix} -4 & 3 \\ -11 & 4 \end{pmatrix}- \textbf{j} \det \begin{pmatrix} 1 & 3 \\ -4 & 4\end{pmatrix} +\textbf{k}\begin{pmatrix} 1 & -4 \\ -4 & -11 \end{pmatrix} = \\ \\ & =[-4 \cdot 4 - (-11) \cdot 3]\textbf{i}-[1 \cdot 4 -(-4) \cdot 3]\textbf{j}+[1 \cdot (-11) - (-4)\cdot(-4)]\textbf{k}=\\ \\ & =(-16+33)\textbf{i}-(4+12)\textbf{j}+(-11-16)\textbf{k}=\\ \\ & =17\textbf{i}-16\textbf{j}-27\textbf{k}=\left \langle {17, -16, -27} \right \rangle\end{align*}

Così:

\small \begin{align*} &\textbf{n}=\textbf{m} \land (\textbf{m} \land \overrightarrow{P_0P_1})=\left \langle {1,-4,3} \right \rangle \land \left \langle {17,-16,-27} \right \rangle=\\ \\ & =\det \begin{pmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ 1&-4&3 \\ 17 &-16 & -27\end{pmatrix}=\\ \\ & =\textbf{i}[-4 \cdot (-27) - (-16) \cdot 3]-\textbf{j}[1 \cdot (-27) -17 \cdot 3]+\textbf{k}[1 \cdot (-16)-17 \cdot -4]= \\ \\ & =\textbf{i}(108+48)-\textbf{j}(-27-51)+\textbf{k}(-16+68)=\\ \\ & =156\textbf{i}+78\textbf{j}+52\textbf{k}=\left \langle {156,78,52} \right \rangle\end{align*}

Ora possiamo applicare la formula per il calcolo della distanza tra un punto e una retta nello spazio. Cominciamo con il calcolare il numeratore:

\begin{align*} & |\overrightarrow{P_0P_1} \times \textbf{n}|=|\left \langle {-4,-11,4} \right \rangle \times \left \langle {156,78,52} \right \rangle|=\\ \\ & =|-4 \cdot 156 +(-11)\cdot78+4\cdot52|=|-1274|=1274 \end{align*}

Veniamo al denominatore:

\lVert {\textbf{n}} \rVert=\sqrt{156^2+78^2+52^2}=182

Così in conclusione possiamo calcolare la distanza cercata:

d=\dfrac{ |\overrightarrow{P_0P_1} \times \textbf{n}|}{\lVert {\textbf{n}} \rVert}=\dfrac{1274}{182}=7

Conclusioni

Abbiamo visto come grazie ai concetti relativi alle proiezioni di vettori è possibile determinare una formula per il calcolo della distanza tra un punto e una retta nello spazio. E in modo simile abbiamo in precedenza determinato la formula per il calcolo della distanza tra un punto e un piano nello spazio.

Nella prossima lezione ci occuperemo di come calcolare la distanza tra due rette nello spazio, ancora utilizzando quanto sappiamo sulle proiezioni di vettori. Buon proseguimento!