Nel termine “disgiunzione inclusiva (OR)” indichiamo esplicitamente l’aggettivo “inclusiva“. Non ci limitiamo quindi a parlare semplicemente di “disgiunzione” e la ragione è ben precisa. Come vedremo nella prossima lezione, infatti, esiste un’altra operazione logica, la disgiunzione esclusiva (XOR).
Come per le altre operazioni sin qui presentate, studieremo il comportamento della disgiunzione inclusiva sia nel caso delle proposizioni chiuse, sia nel caso delle proposizioni aperte. E in quest’ultimo caso, vedremo come la disgiunzione inclusiva sia legata all’operazione di unione tra insiemi.
Definizione di disgiunzione inclusiva (OR)
Introduciamo l’operazione di disgiunzione inclusiva riferendoci, per ora, al solo caso di proposizioni chiuse.
Assegnate quindi due proposizioni chiuse \( a \) e \( b \), l’operazione di disgiunzione inclusiva si indica con la notazione:
\[ a \vee b \]
e si legge “\( a \) oppure \( b \)”.
In alternativa, il simbolo di disgiunzione inclusiva può essere letto come “o” o anche “vel” (termine che deriva dal latino). Un’alternativa è anche l’uso del termine “OR”, molto diffuso nell’elettronica e nella programmazione. Così le espressioni logiche:
\[ a \: \text{o} \:b; \qquad a \: \: \text{OR}\:\: b \]
si riferiscono equivalentemente alla disgiunzione inclusiva tra le due proposizioni \( a \) e \( b \).
L’operazione fornisce come risultato una proposizione molecolare, poiché come la congiunzione opera su due proposizioni. Per cui la proposizione risultato avrà almeno due predicati 😉
La proposizione ottenuta dall’operazione di disgiunzione inclusiva è vera se almeno una delle due proposizioni \( a \) e \( b \) è vera. Il risultato dell’operazione è quindi una proposizione vera anche nel caso in cui entrambe le proposizioni sono vere.
La proposizione risultato della disgiunzione inclusiva è falsa nel solo caso in cui entrambe le proposizioni sono false.
La tavola di verità dell’operazione disgiunzione inclusiva è la seguente:
Tavola di verità della disgiunzione inclusiva (proposizioni chiuse)

Date ad esempio le seguenti proposizioni atomiche:
a: “New York è una città americana”
b: “Bangkok è la capitale della Thailandia”
effettuando la disgiunzione inclusiva tra le due proposizioni otteniamo:
\( a \vee b\): “New York è una città americana oppure Bangkok è la capitale della Thailandia”
La proposizione molecolare ottenuta è vera poiché almeno una delle due proposizioni \( a, \: b \) che la compongono è vera. In questo particolare caso, infatti, sono vere entrambe le proposizioni.
Come ulteriore esempio, consideriamo le due proposizioni:
a: “Il coccodrillo è un volatile”
b: “I mesi dell’anno sono dodici”
La proposizione \( a \vee b \) è:
\( a \vee b \): “Il coccodrillo è un volatile o i mesi dell’anno sono dodici.”
Questa è vera poiché almeno una delle due proposizioni è vera. Infatti, la proposizione \( a \) è falsa ma la proposizione \( b \) è vera.
Come ultimo esempio, date le proposizioni \( a:\text{“5 < 2”} \) e \( b:\text{“-10 > 0”} \), la proposizione \( a \vee b \) è falsa poiché entrambe le proposizioni \( a \) e \( b \) sono false.
Disgiunzione inclusiva nel caso di proposizioni aperte
Immaginiamo ora di avere due proposizioni aperte \( a(x) \) e \( b(x) \). Supponiamo altresì che entrambe le proposizioni abbiano come dominio l’insieme \( D \).
Indichiamo con \( A\) l’insieme di verità della proposizione \( a(x) \) e con \( B \) l’insieme di verità della proposizione \( b(x) \). Con ciò intendiamo che la proposizione \( a(x) \) è vera sostituendo alla \( x \) uno qualsiasi degli elementi dell’insieme \( A \). Intendiamo inoltre che la proposizione \( b(x) \) è vera sostituendo alla \( x \) uno qualsiasi degli elementi dell’insieme \( B. \)
Ora, ci chiediamo di valutare l’espressione logica:
\[ a(x) \vee b(x) \]
Ora, la proposizione \( a (x) \vee b(x) \) sarà vera per quei valori della \( x \) in corrispondenza dei quali almeno una delle due proposizioni \( a(x) \) e \( b(x) \) risulta vera.
L’insieme di verità della proposizione \( a (x) \vee b(x) \) è quindi dato da tutti gli elementi \( x \) che appartengono all’insieme di verità della proposizione \( a(x) \) oppure all’insieme di verità della proposizione \( b(x) \).
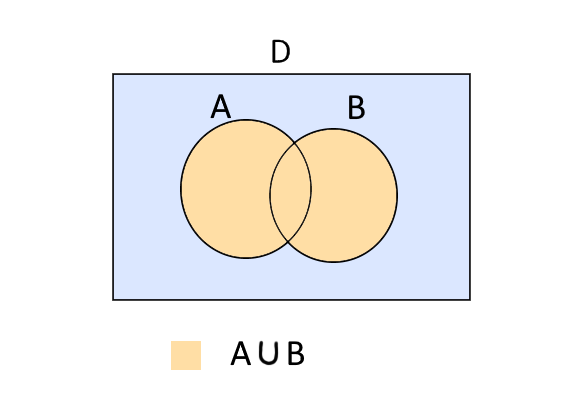
Quindi, utilizzando la definizione di insieme unione, possiamo dire che l’insieme di verità della proposizione \( a (x) \vee b(x) \) è dato dall’unione tra l’insieme di verità di \( a(x) \) e l’insieme di verità di \( b(x) \). In simboli:
\[ a(x) \vee b(x) \quad \text{e’ vera per tutti gli }x \: \text{dell’insieme} \quad A \cup B \]
Dunque, per determinare il valore di verità della proposizione ottenuta dalla disgiunzione inclusiva di due proposizioni aperte, basta effettuare l’unione degli insiemi di verità delle singole proposizioni di partenza.
Qui termina questa lezione relativa alla disgiunzione inclusiva (OR). Nella prossima lezione vedremo la sua “cugina”, ovvero la disgiunzione esclusiva (XOR). Quest’ultima è simile alla disgiunzione inclusiva, ma come si capisce dal differente nome c’è un’importante differenza. Ciao a tutti! 🙂
