La congiunzione logica può operare sia con proposizioni aperte, sia con proposizioni chiuse. Quindi, come nel caso della negazione, studieremo entrambi i casi.
Definizione di congiunzione logica
Introduciamo l’operazione di congiunzione logica riferendoci, per ora, al solo caso di proposizioni chiuse.
Assegnate due proposizioni chiuse \( a \) e \( b \), l’operazione di congiunzione logica si indica con la notazione:
\[ a \wedge b \]
e si legge “\( a \) e \( b \)”.
In alternativa, si possono anche usare i simboli \( \text{et} \) oppure \( \text{AND} \), il primo usato in matematica, il secondo più che altro nell’elettronica e nella programmazione. Così le espressioni logiche:
\[ a \: \text{et} \:b; \qquad a \: \: \text{AND}\:\: b \]
si riferiscono equivalentemente alla congiunzione logica tra le due proposizioni \( a \) e \( b \).
L’operazione fornisce come risultato una proposizione molecolare. Ciò è ovvio poiché combinando tra loro due proposizioni otterremo una proposizione che avrà almeno due predicati.
La proposizione ottenuta dall’operazione di congiunzione è vera soltanto se sono vere entrambe le proposizioni \( a \) e \( b \). E’ quindi falsa in tutti gli altri casi.
La tavola di verità dell’operazione congiunzione logica è la seguente:
Tavola di verità della congiunzione logica (proposizioni chiuse)

Così ad esempio, date le proposizioni atomiche:
a:“L’Italia è uno stato europeo”
b:”Berlino è la capitale della Germania”
effettuando la congiunzione logica tra le due proposizioni otteniamo:
\( a \wedge b \): “L’Italia è uno stato europeo e Berlino è la capitale della Germania”
La proposizione molecolare ottenuta è vera poiché entrambe le proposizioni \( a, \: b \) che la compongono sono vere.
Osserviamo che l’unica cosa che conta è il valore di verità delle singole proposizioni e non il significato che la proposizione risultato dell’operazione ha nel linguaggio comune. Ad esempio, date le proposizioni:
a: “Lo smartphone è un dispositivo elettronico”
b: “8 è un numero dispari”
la proposizione molecolare che otteniamo con la congiunzione logica:
\( a \wedge b: \)”Lo smartphone è un dispositivo elettronico e 8 è un numero dispari”
è falsa poiché la proposizione \( a \) è vera mentre la proposizione \( b \) è falsa.
Ora, uno smartphone non ha molto a che vedere con la presunta disparità di un numero! Quindi, secondo il senso comune una frase del genere non ha alcun significato. Come detto, però, dobbiamo considerare unicamente il valore di verità di ciascuna proposizione di partenza.
Congiunzione nel caso di proposizioni aperte
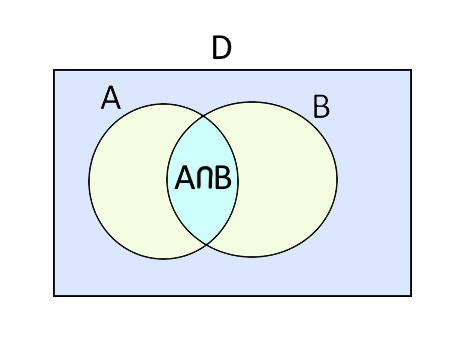
Supponiamo ora di avere due proposizioni aperte \( a(x) \) e \( b(x) \). Supponiamo inoltre che entrambe le proposizioni abbiano come dominio l’insieme \( D \).
Indichiamo con \( A\) l’insieme di verità della proposizione \( a(x) \) e con \( B \) l’insieme di verità della proposizione \( b(x) \). In altre parole, la proposizione \( a(x) \) è vera sostituendo alla \( x \) uno qualsiasi degli elementi dell’insieme \( A \). Inoltre, la proposizione \( b(x) \) è vera sostituendo alla \( x \) uno qualsiasi degli elementi dell’insieme \( B \).
Ora, ci chiediamo di valutare l’espressione logica:
\[ a(x) \wedge b(x) \]
Ora, la proposizione \( a (x) \wedge b(x) \) sarà vera soltanto per quei valori della \( x \) in corrispondenza dei quali entrambe le proposizioni \( a(x) \) e \( b(x) \) risultano vere.
L’insieme di verità della proposizione \( a (x) \wedge b(x) \) è quindi dato da tutti gli elementi \( x \) che appartengono sia all’insieme di verità della proposizione \( a(x) \), sia all’insieme di verità della proposizione \( b(x) \).
Ora, utilizzando la definizione di insieme intersezione, possiamo affermare che l’insieme di verità della proposizione \( a (x) \wedge b(x) \) è dato dall’intersezione tra l’insieme di verità di \( a(x) \) e l’insieme di verità di \( b(x) \). In simboli:
\[ a(x) \wedge b(x) \quad \text{e’ vera per tutti gli }x \: \text{dell’insieme} \quad A \cap B \]
Dunque, per determinare il valore di verità della proposizione ottenuta dalla congiunzione di due proposizioni aperte, basta effettuare l’intersezione degli insiemi di verità delle singole proposizioni di partenza.
Abbiamo così fatto la conoscenza della operazione congiunzione logica, sia per il caso delle proposizioni chiuse, sia per il caso delle proposizioni aperte. Nella prossima lezione, presenteremo una nuova operazione logica: la disgiunzione inclusiva (OR). Ciao a tutti! 🙂
