In termini semplici, la domanda che ci porremo è: che relazione abbiamo tra i valori del coefficiente della \( x \) e del termine noto e l’esistenza o meno di una soluzione per l’equazione data?
Per la verità, già abbiamo visto questi aspetti quando abbiamo introdotto i principi di equivalenza e abbiamo svolto gli esercizi sulle equazioni di primo grado. Tuttavia, ora vogliamo spiegare in forma generale quanto abbiamo già visto in casi specifici. 🙂
Vediamo allora anche con esercizi svolti come si effettua la discussione di un’equazione di primo grado.
Discussione di un’equazione di primo grado a partire dalla forma normale
Sia data un’equazione di primo grado in forma normale, ovvero espressa in generale come:
\[ ax=b \]
Sappiamo che la sua eventuale soluzione è data da:
\[ x = \dfrac{b}{a} \]
Diciamo eventuale poiché la soluzione può non esistere. Oppure, possiamo avere come soluzione un qualsiasi valore. Vogliamo ora mostrare che ciò dipende dal valore dei coefficienti \( a \) e \( b \).
Per effettuare la discussione dell’equazione dobbiamo considerare tre casi.
Primo caso
Supponiamo che il coefficiente della \( x \) sia diverso da zero e che sia anche \( b \) diverso da zero. Se valgono tali ipotesi, esiste una soluzione, data da \( x=\dfrac{b}{a} \).
Nel caso particolare in cui sia ancora \( a \) diverso da zero ma sia \( b=0 \), abbiamo la soluzione \( x=0 \). L’equazione è cioè soddisfatta da un valore nullo della \( x \).
In entrambe le circostanze, una soluzione esiste ed è unica. Così, l’equazione si dice determinata.
Secondo caso
Se \( a \) è uguale a zero e \( b \) è diverso da zero, ci ritroviamo con l’uguaglianza:
\[ 0x = b \]
Una tale uguaglianza non è mai verificata, poiché non esiste nessun numero che moltiplicato per zero è diverso da zero. Allora, l’equazione non ammette soluzione ed è impossibile. Qualunque valore attribuiamo alla \( x \), otteniamo in questo caso sempre un’uguaglianza falsa. Ad esempio, se \( b=2 \) e sostituiamo alla \( x \) il valore \( 7 \) abbiamo:
\[ 0 \cdot 7 = 2 \]
uguaglianza evidentemente falsa.
Terzo caso
Consideriamo ora la circostanza ove \( a \) e \( b \) siano entrambi nulli. In tal caso abbiamo:
\[ 0 \cdot x = 0 \]
Osserviamo che qualunque valore attribuiamo alla \( x \) l’uguaglianza sarà verificata. A questo punto l’equazione si può assimilare ad una identità e l’equazione è in conclusione verificata per qualunque valore della \( x \).
Diciamo così che l’equazione è indeterminata.
Possiamo in conclusione riassumere la discussione di un’equazione di primo grado data in forma normale con la seguente mappa concettuale:
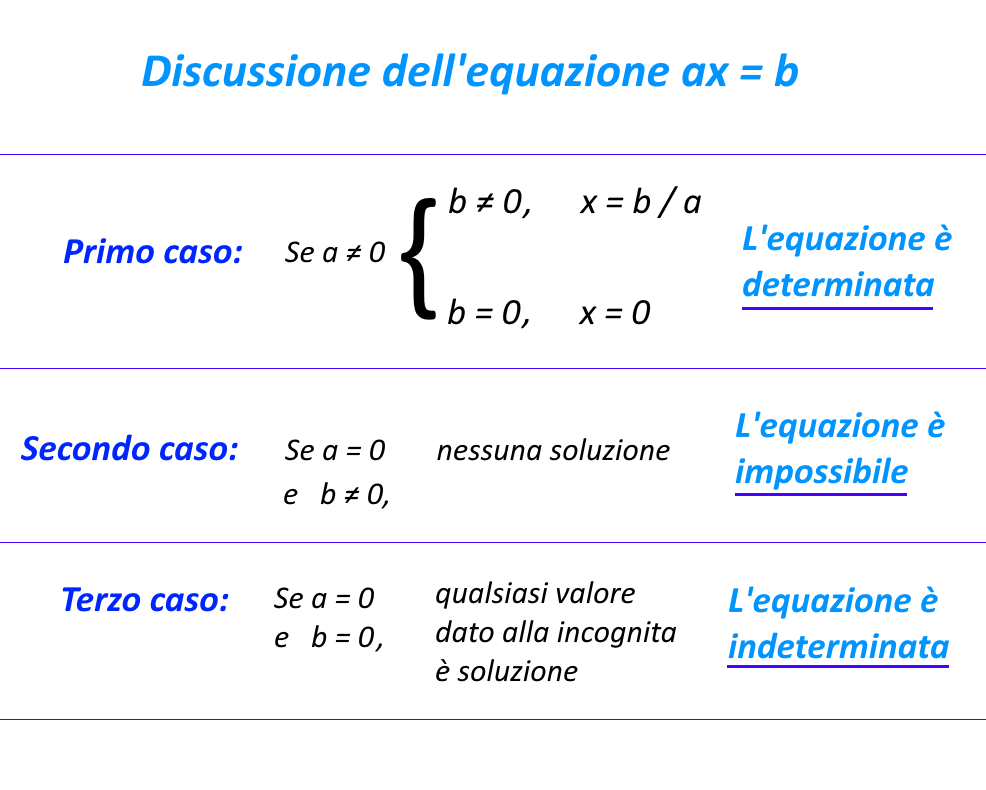Vediamo ora degli esempi che comprendono nel loro insieme tutti e tre i casi. 😉
Esempio 1
\[ 3x=5+x+2x \]
Eseguiamo i calcoli al secondo membro, sommando tra loro i termini simili:
\[ 3x=5+3x \]
ovvero:
\[ 3x-3x=5 \]
e quindi:
\[ 0=5 \]
L’uguaglianza è evidentemente falsa. Per meglio comprendere, possiamo intendere il primo membro come \( 0x \). L’equazione sarà quindi:
\[ 0x=5 \]
Siamo allora nel secondo caso della mappa concettuale, poiché \( a = 0 \) e \( b = 5 \). L’equazione è pertanto impossibile. Non esiste infatti nessun valore della \( x \) che può verificare l’uguaglianza.
Esempio 2
\[ 2x+3=x+x+3 \]
L’equazione diventa:
\[ 2x-2x=3-3 \]
ovvero:
\[ 0 = 0 \]
Ancora, indicando esplicitamente al primo membro l’incognita \( x \):
\[ 0x=0 \]
Siamo nel caso in cui \( a=0 \) e \( b=0 \), di conseguenza l’equazione è indeterminata. Infatti, ogni valore attribuito alla \( x \) è soluzione dell’equazione. Ciò è intuitivo, poiché un qualsiasi numero moltiplicato per zero dà zero. 😉
Esempio 3
\[ 9(x+1)=7(x-3)+30 \]
Calcoliamo i prodotti al primo membro e al secondo membro:
\[ 9x+9=7x-21+30 \]
Trasportando dei termini e poi sommando i termini simili otteniamo:
\[ 9x-7x=-9-21+30 \]
ovvero:
\[ 2x=0 \]
e in conclusione:
\[ x=0 \]
Siamo nel caso in cui \( a \neq 0 \) e \( b = 0 \). L’equazione è determinata con soluzione uguale a zero.
Esempio 4
\[ 2(3x+2)-(11x+7)=3(1-x) \]
Si ha:
\[ 6x+4-11x-7= 3-3x\]
\[ -2x=3-4+7 \]
\[ -2x=6 \]
\[ 2x=-6 \]
\[ x=-3 \]
Abbiamo \( a \) e \( b \) entrambi diversi da zero e l’equazione ammette una soluzione diversa da zero. L’equazione è soddisfatta per \( x=-3 \) ed è determinata.
Qui finisce questa lezione sulla discussione di un’equazione di primo grado. Nella prossima lezione, vedremo le equazioni di primo grado in un’incognita a termini frazionari.
Ciao a tutti e buono studio con Altramatica! 🙂