La scomposizione in fattori primi consiste nell’esprimere un numero naturale come il prodotto di altri particolari numeri, come vedremo fra un istante.
Teorema fondamentale dell’aritmetica
Cominciamo questa lezione con l’introdurre un importante teorema, noto come teorema fondamentale dell’aritmetica. Questo teorema afferma che (prima parte):
ogni numero naturale maggiore di 1 è primo oppure può essere scritto come prodotto di fattori che sono tutti numeri primi.
Ad esempio, il numero \( 21 \) si può esprimere come prodotto dei fattori \( 3 \times 7 = 21 \). Entrambi i fattori sono numeri primi. Ancora, il numero \( 48 \) si può esprimere come il prodotto dei fattori \( 2 \times 2 \times 2\times 2 \times 3 \). Come possiamo vedere, ancora una volta i fattori sono tutti numeri primi.
La seconda parte del teorema ci dice che:
la rappresentazione di un numero naturale maggiore di 1 come prodotto di numeri tutti primi è unica se non consideriamo l’ordine nel quale compaiono i fattori.
E ciò che si fa in matematica è proprio non considerare l’ordine dei fattori. In altre parole, diremo che ad esempio \( 21 = 3 \times 7 \) è un modo unico di esprimere \( 21 \) come prodotto di numeri primi. Così, conveniamo che affermare \( 21 = 7 \times 3 \) è la stessa cosa.
Quello che conta sono quindi i singoli fattori primi e non l’ordine con il quale li scriviamo 😉 Per cui i prodotti \( 3 \times 7 \) e \( 7 \times 3 \) sono la stessa rappresentazione del numero \( 21 \).
Una rappresentazione di questo tipo si dice scomposizione di un numero in fattori primi.
Esempi
Esempio 1
Consideriamo il numero \( 27 \). Questo si può esprimere come prodotto di fattori primi (diciamo, può essere scomposto in fattori primi) soltanto come:
\[ 27 = 3 \times 3 \times 3 \]
Questo è l’unico prodotto di fattori primi che rappresenta il numero \( 27 \). Osserviamo che \( 27 \) si può esprimere anche con il prodotto:
\[ 27 = 9 \times 3 \]
ma questa non è una scomposizione di un numero in fattori primi, poiché \( 9 \) non è infatti un numero primo. L’unica scomposizione in numeri tutti primi del numero \( 27 \) è quella già scritta in precedenza.
Esempio 2
Il numero \( 72 \) si scompone in fattori primi come:
\[ 72 = 2 \times 2\times 2\times 3 \times 3 \]
Osserviamo che esistono più prodotti tra numeri che equivalgono a \( 72 \):
\[ 72 = 4 \times 2 \times 9; \qquad 72 = 8 \times 9 ; \dots \]
ma in questi ultimi prodotti abbiamo fattori che non sono tutti primi.
Chiariamo ancora che l’ordine dei fattori primi non conta. Così i prodotti:
\[ 72 = 2 \times 2\times 2\times 3 \times 3; \qquad 72 = 3 \times 3 \times 2 \times 2\times 2 \]
rappresentano la stessa scomposizione in fattori primi.
Ora la domanda è: come si riescono a trovare i numeri primi tramite i quali scomporre un numero in fattori primi?
Divisibilità per i numeri primi
Poiché ogni numero può essere rappresentato dal prodotto di numeri primi, sicuramente ogni numero sarà divisibile per almeno un numero primo.
In particolare, avremo che ogni numero sarà divisibile per ciascun fattore della sua scomposizione in fattori primi 😉
Per poter scrivere la scomposizione in fattori primi di un numero, è dunque chiaro che dovremo anzitutto trovare tutti i numeri primi per i quali è divisibile. Dobbiamo dunque introdurre alcuni criteri di divisibilità, cioè delle regole che ci permettono di capire se un numero dato è divisibile o meno per un certo numero primo.
Criteri di divisibilità (per numeri primi, semplificati)
Vediamo alcune semplici regole.
- Un numero è divisibile per due se la cifra delle unità è divisibile per \( 2 \). Così se un numero ha la cifra delle unità pari a \( 0,2,4,6,8 \) allora è divisibile per \( 2 \).
- Un numero è divisibile per \( 3 \) se la somma delle sue cifre è un numero divisibile per \( 3 \). Così il numero \( 27 \) è divisibile per \( 3 \) poiché \( 2+7=9 \). Il numero \( 9 \) è ovviamente divisibile per \( 3 \) poiché fa parte dei risultati della tabellina del \( 3. \)
- Un numero è divisibile per \( 5 \) se la sua ultima cifra è \( 5 \) oppure \( 0 \).
- Un numero è divisibile per \( 7 \) (regola semplificata) se almeno fa parte dei risultati della tabellina del \( 7 .\) Così, \( 49 \) è divisibile per \( 7 \) poiché \( 7 \times 7 = 49 \).
- Un numero è divisibile per \( 11 \) (regola semplificata) se almeno le cifre che lo compongono sono tra loro uguali. Avremo quindi che il numero \( 77 \) è divisibile per \( 11. \)
Queste sono le regole essenziali, il minimo sindacale per i criteri di divisibilità. Ci occuperemo più avanti di presentare i criteri di divisibilità in modo completo e generale, tuttavia sappiate che queste regole sono sufficienti per poter operare le nostre prime scomposizioni in fattori primi 😉
Metodo per scomporre in fattori primi un numero dato
Sia da scomporre in fattori primi il numero \( 76 \).
Tracciamo una linea verticale un po’ scostata verso destra, in modo da avere spazio per scrivere dei numeri sia a sinistra, sia a destra della linea.

Scriviamo in alto a sinistra il numero dato, cioè il numero da scomporre in fattori primi:

Ora, per quale numero è divisibile \( 76 \)? Osserviamo che è divisibile per \( 2 \) poiché la cifra delle unità (6) è divisibile per \( 2 \). Scriviamo questo divisore nella parte a destra della linea verticale:

Ora, scriviamo a sinistra della linea, sotto il \( 76 \), il risultato della divisione \( 76:2=38 \):

A questo punto, dobbiamo trovare un divisore di \( 38 \). Poiché la sua cifra delle unità è divisibile per \( 2 \), anche questo numero risulta divisibile per \( 2 \). Scriviamo quindi il divisore (\( 2 \)) a destra della linea:

Inoltre scriviamo il risultato della divisione \( 38:2=19 \) a sinistra della linea:

Ora, \( 19 \) è un numero primo (vedi tabella dei numeri primi), per cui lo dividiamo con sé stesso:

Ora dobbiamo scrivere il risultato della divisione \( 19:19 = 1 \), cone negli altri casi a sinistra della linea verticale:

Arrivati ad ottenere un risultato \( 1 \), il procedimento si arresta. A destra della linea verticale ci ritroviamo tutti i fattori primi il cui prodotto è uguale al numero dato.
Di conseguenza, potremo scrivere la scomposizione in fattori primi del numero assegnato. Si ha:
\[ 76 = 2 \times 2 \times 19 \]
Abbiamo dunque trovato la scomposizione in fattori primi del numero \( 76 \). 🙂
Uso delle potenze nello scrivere la scomposizione in fattori primi
Osserviamo che la scomposizione in fattori primi:
\[ 76 = 2 \times 2 \times 19 \]
può essere scritta in modo più compatto utilizzando le potenze:
\[ 76 = 2^2 \times 19 \]
In generale, potremo scrivere la scomposizione di un numero in fattori primi scrivendo una sola volta ciascun fattore primo, ognuno elevato all’esponente pari al numero di volte che il fattore compare nella scomposizione.
Così, ad esempio, data la seguente scomposizione in fattori primi:
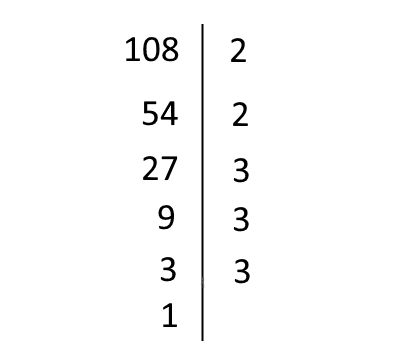
osserviamo che il numero \( 2 \) compare due volte mentre il numero \( 3 \) compare tre volte. Di conseguenza scriveremo, con le potenze:
\[ 108=2^2 \times 3^3 \]
Per quanto riguarda la scomposizione di un numero in fattori primi direi che è tutto. Nella prossima lezione vedremo il Massimo Comune Divisore. Ciao a tutti e buono studio con Altramatica! 🙂
