Il confronto tra infiniti è utile per farci capire quanto velocemente una funzione tende ad infinito (diverge) rispetto ad un’altra (anch’essa tendente ad infinito – o divergente). Un tale confronto si rivelerà importante nella risoluzione di moltissimi esercizi.
In questa lezione riprenderemo i concetti di funzioni infinite e vedremo come il confronto tra infiniti si presta molto bene allo studio della forma indeterminata \( \dfrac{\infty}{\infty} \). Ma non solo, come vedremo nella prossima lezione.
Confronto tra infiniti – ordine di infinito
Non tutte le funzioni infinite tendono ad infinito, per \( x \) che tende ad uno stesso \( x_0 \), con la stessa velocità. Ad esempio, le funzioni \( y=x^2 \) e \( y=x^3 \) sono entrambe infinite per \( x \to +\infty\):
\[ \lim_{x \to +\infty} x^2 = +\infty; \qquad \lim_{x \to +\infty}x^3=+\infty \]
Tuttavia, confrontando i rispettivi grafici capiamo subito che il loro comportamento è differente:
Possiamo vedere chiaramente come la funzione \( y=x^3 \) tende ad infinito più rapidamente rispetto a \( y=x^2 \). La funzione \( y=x^3 \), cioè, cresce più rapidamente della funzione \( y=x^2 \). Infatti, vediamo che a partire da un valore della \( x \) sufficientemente grande si ha sempre che \( x^3>x^2 \).
Come si può descrivere formalmente questo comportamento? Come nel caso degli infinitesimi, anche qui l’idea è quella di confrontare tra loro i due differenti modi con i quali le funzioni raggiungono il comune valore del limite.
Ci vengono in aiuto le seguenti definizioni, ed in particolare – ve lo anticipo – in questo caso diremo che la funzione \( y=x^3 \) è infinita di ordine superiore rispetto a \( y=x^2 \).
Per tutte le seguenti definizioni valgono le ipotesi che \( f(x) \) e \( g(x) \) siano due funzioni infinite per \( x \to x_0 \), cioè:
\[ \lim_{x \to x_0}f(x)=\pm \infty; \qquad \lim_{x \to x_0}g(x)=\pm\infty \]
Supponiamo inoltre l’esistenza del limite:
\[ \lim_{x \to x_0}\dfrac{f(x)}{g(x)} \]
Infine, \( x_0 \) può assumere sia un valore reale, sia \( +\infty \) o \( -\infty \).
Definizione (infinito di ordine superiore)
Si dice che una funzione \( f(x) \) è un infinito di ordine superiore rispetto a \( g(x) \) se:
\[ \lim_{x \to x_0} \dfrac{f(x)}{g(x)}=\pm \infty \]
Con la scrittura \( \pm \infty \) intendiamo che il limite, ovviamente unico, potrà essere \( +\infty \) o \( -\infty \) in base ai segni dei due infiniti.
Notiamo comunque che a prescindere che il risultato del limite sia più infinito o meno infinito, comunque \( f(x) \) risulterà un infinito di ordine superiore rispetto a \( g(x) \). Di conseguenza, visto che il segno del risultato non è determinante, la precedente condizione di limite può anche essere riscritta come:
\[ \lim_{x \to x_0} \dfrac{\left|f(x)\right|}{\left|g(x)\right|}= + \infty \]
In tal caso “forziamo positivi” i due infiniti grazie alla funzione modulo 😉 E questo è ciò che avevamo fatto anche per gli infinitesimi, nel caso in cui la funzione a numeratore era un infinitesimo di ordine inferiore.
Definizione (infinito di ordine inferiore)
Si dice che una funzione \( f(x) \) è un infinito di ordine inferiore rispetto a \( g(x) \) se:
\[ \lim_{x \to x_0} \dfrac{f(x)}{g(x)}= 0 \]
In questo caso la funzione a denominatore cresce più velocemente di quella a numeratore. \( f(x) \) è dunque un infinito di ordine inferiore poiché cresce più lentamente di \( g(x) \).
Definizione (infiniti dello stesso ordine)
Si dice che \( f(x) \) e \( g(x) \) sono funzioni infinite dello stesso ordine se:
\[ \lim_{x \to x_0} \dfrac{f(x)}{g(x)}=l \neq 0, \quad l \in \mathbb{R} \]
e cioè se il limite appena scritto ha come risultato un valore finito (numero) diverso da 0.
Definizione (infiniti non confrontabili)
Se il limite
\[ \lim_{x \to x_0}\dfrac{f(x)}{g(x)} \]
non esiste, allora i due infiniti \( f(x) \) e \( g(x) \) non sono confrontabili. Di conseguenza, risulterà impossibile stabilire un ordine di infinito tra una funzione e l’altra.
Esempi
Vediamo ora come calcolare dei semplici limiti utilizzando le definizioni appena fornite 😉
Esempio 1
Calcolare:
\[ \lim_{x \to +\infty}\dfrac{x^5}{x^2} \]
Osserviamo che siamo nel caso della forma indeterminata \( \dfrac{+\infty}{+\infty} \), poiché entrambe le funzioni a numeratore e denominatore sono infinite per \( x \to +\infty \). Tuttavia, l’esercizio si risolve agevolmente osservando che \( x^5 \) è un infinito di ordine superiore rispetto ad \( x^2 \). Infatti, per \( x \to +\infty \) una funzione potenza con esponente più grande cresce più rapidamente di una funzione potenza con esponente più piccolo:
\( x^5 \) è dunque un infinitesimo di ordine superiore rispetto ad \( x^2 \). Pertanto, per la definizione di infinito di ordine superiore si ha che:
\[ \lim_{x \to +\infty}\dfrac{x^5}{x^2}=+\infty \]
ESEMPIO 2
Calcolare:
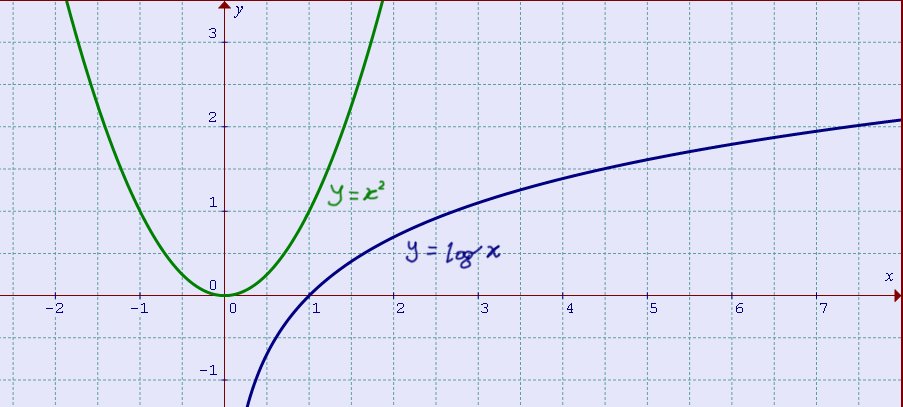
\[ \lim_{x \to +\infty}\dfrac{\log(x)}{x^2} \]
Entrambe le funzioni \( y =x^2 \) e \( y=\log x \) sono infinite per \( x \to +\infty \). Siamo dunque in presenza della forma indeterminata \( \dfrac{+\infty}{+\infty} \).
Confrontiamo l’andamento della funzione \( y =\log(x) \) con quello della funzione \( y=x^2 \):
Si può chiaramente notare dal grafico che per \( x \) che tende ad infinito la funzione \( y=x^2 \) cresce molto più rapidamente della funzione \( y=\log x \). Di conseguenza, possiamo dire che \( y=x^2 \) è infinita di ordine superiore rispetto a \( y=\log x \). Pertanto, la funzione al numeratore (\( y=\log x \)) è un infinito di ordine inferiore rispetto alla funzione al denominatore (\( y=x^2 \)) e si ha in conclusione:
\[ \lim_{x \to +\infty}\dfrac{\log(x)}{x^2}=0 \]
Per convincersene basta riguardare la definizione di infinitesimo di ordine inferiore 😉
Esempio 3
Calcolare:
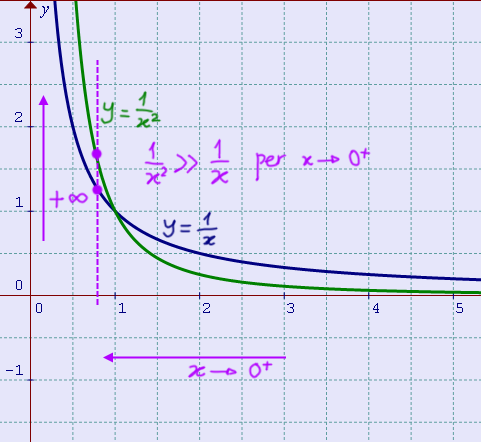
\[ \lim_{x \to 0^+} \dfrac{\dfrac{1}{x}}{\dfrac{1}{x^2}} \]
Osserviamo anzitutto che le definizioni di funzione infinita (e infinitesima) valgono anche per limiti destri e sinistri, così come i concetti di ordini di infinito (e infinitesimo).
Entrambe le funzioni a numeratore e denominatore tendono a \( +\infty \) per \( x \) che tende a 0 da destra. Per vederlo possiamo osservare, per i termini a denominatore di ciascuna funzione, che il limite del reciproco di una funzione è uguale al reciproco del limite della funzione stessa (vedi operazioni sui limiti). E’ utile inoltre ricordarci che per l’algebra degli infiniti ed infinitesimi, \( \dfrac{1}{0^+}=+\infty \)).
Per il limite assegnato, abbiamo dunque la forma indeterminata del tipo \( \dfrac {+\infty}{+\infty} \).
Osserviamo, sempre nel limite assegnato, che la funzione a numeratore (\( y=\dfrac{1}{x} \)) tende ad infinito più lentamente della funzione a denominatore (\( y=\dfrac{1}{x^2} \)):
La funzione a numeratore è dunque un infinito di ordine inferiore rispetto a quella a denominatore e si ha, in conclusione:
\[ \lim_{x \to 0^+} \dfrac{\dfrac{1}{x}}{\dfrac{1}{x^2}}=0 \]
Lascio a voi verificare cosa succede per il limite sinistro (sempre con \( x_0=0 \)), e quindi trarre le conclusioni per il limite bilatero 😉
Per risolvere questo tipo di limiti appare chiara la necessità di conoscere il comportamento delle funzioni elementari. In particolare, dobbiamo essere in grado di sapere quali funzioni elementari tendono a infinito, al limite, più o meno rapidamente rispetto ad altre.
Tenete poi conto del fatto che nella prossima lezione introdurremo delle regole che ci permetteranno di calcolare i limiti con infiniti e infinitesimi anche nel caso di espressioni più complesse di un semplice rapporto tra funzioni elementari 😉
Confronto del comportamento di funzioni elementari infinite
Il confronto del grafico di funzioni elementari infinite è molto utile come riferimento per risolvere gli esercizi sui limiti. Tale approccio è infatti di aiuto nell’effettuare il confronto tra infiniti. Vediamo alcuni casi.
Premettiamo che con la notazione:
\[ f(x) >> g(x) \qquad \text{per} \quad x \to x_0 \]
intendiamo dire che, per \( x \to x_0 \), \( f(x) \) è un infinito di ordine superiore rispetto a \( g(x) \), ovvero che \( f(x) \) tende ad infinito molto più rapidamente di \( g(x) \). Detta in altri termini, intendiamo che per ogni valore della \( x \) sufficientemente “prossimo” ad \( x_0 \), abbiamo che \( f(x) > g(x) \).
Per la funzione esponenziale, osserviamo che:
\[ a^x>b^x \quad \text{per} \: x \to +\infty \quad \text{con} \quad a > b, \quad a, b > 1 \]
ovvero \( a^x \) è un infinito di ordine superiore rispetto a \( b^x \) per \( x \to +\infty \) se la base \( a \) è maggiore della base \( b \) (discorso valido con basi maggiori di 1).
Il confronto dei grafici nella figura seguente mostra chiaramente che \( y=a^x \) cresce più rapidamente rispetto ad \( y=b^x \), per \( a>b \).
Per la funzione potenza, osserviamo che:
\[ x^p>>x^q, \quad {per} \: x \to +\infty, \quad p > q, \quad p, q \in \mathbb{R^+} \]
Il seguente grafico mostra il caso nel quale \( p=5\) e \( q=2 \):
Per brevità abbiamo presentato la relazioni con esponenti reali (includendo quindi il caso degli esponenti interi e razionali). E’ possibile comunque riscrivere le relazioni adottando esplicitamente esponenti interi e razionali, come abbiamo fatto nella precedente lezione per gli infinitesimi 😉
Confrontando i grafici delle funzioni esponenziali con i grafici delle funzioni potenza è abbastanza immediato rendersi conto che:
\[ a^x>>x^p, \qquad a>1, \qquad p \:\in \mathbb{R^+},\quad x \to +\infty \]
Osserviamo che per \( x \to +\infty \) la funzione \( y=\log(x) \) tende ad infinito più lentamente rispetto alle funzioni esponenziale e potenza (basta un confronto dei grafici per convincersene). Possiamo dunque scrivere la seguente gerarchia per gli infiniti, utile per stabilire qual’è l’infinito di ordine maggiore fra le funzioni infinite da analizzare in un dato momento:
\[ a^x>>x^p>> \log x, \qquad a>1, \quad p \in \mathbb{R^+}, \qquad x \to +\infty \]
Qui finisce la lezione sul confronto tra infiniti. Nella prossima lezione vedremo delle regole per poter applicare le tecniche di confronto tra infinitesimi e confronto tra infiniti e casi più generali dei semplici rapporti tra funzioni elementari. Vedremo cioè come ricavare la parte principale di infiniti ed infinitesimi.
Buono studio a tutti con Altramatica! 🙂