In particolare, gli asintoti orizzontali sono rette orizzontali, cioè rette di equazione \( y = l \), ove \( l \) è un numero reale. E, per \( x \) che tende ad infinito, tali rette approssimano il grafico della funzione. Come vedremo, affinché ciò accada \( l \) dovrà essere proprio il limite finito della funzione per \( x \) che tende a più infinito e/o meno infinito.
Detta in modo intuitivo, se una funzione ha un asintoto orizzontale ad esempio per \( x \to +\infty \), il suo grafico potrà essere approssimato “nelle vicinanze” di più infinito con una retta orizzontale che è proprio l’asintoto orizzontale.
Asintoti orizzontali: definizioni
Sia data una funzione \( f(x) \) definita in \( D_f \subseteq \mathbb{R} \) e a valori in \( \mathbb{R} \), con \( D_f \) illimitato.
Sia ad esempio \( D_f= ]-\infty, a[ \:\: \cup \:\: ]b, +\infty[, \: a, \: b \in \mathbb{R} \). Il dominio della funzione sia cioè un insieme illimitato sia inferiormente, sia superiormente.
Si dice che la retta (orizzontale) \( y=l_1 \) è asintoto orizzontale sinistro per la funzione \( f(x) \) se:
\[ \lim_{x \to -\infty}f(x)=l_1, \quad l_1 \in \mathbb{R} \]
Si dice che la retta \( y=l_2 \) è asintoto orizzontale destro per la funzione \( f(x) \) se:
\[ \lim_{x \to +\infty}f(x)=l_2, \quad l_2 \in \mathbb{R} \]
Si dice che la retta \( y=l \) è asintoto orizzontale bilatero per la funzione se:
\[ \lim_{x \to -\infty}f(x)=\lim_{x \to +\infty}f(x)=l \in \mathbb{R} \]
cioè l’asintoto orizzontale per la funzione è bilatero se i due limiti \( l_1 \) e \( l_2 \) sono uguali e finiti.
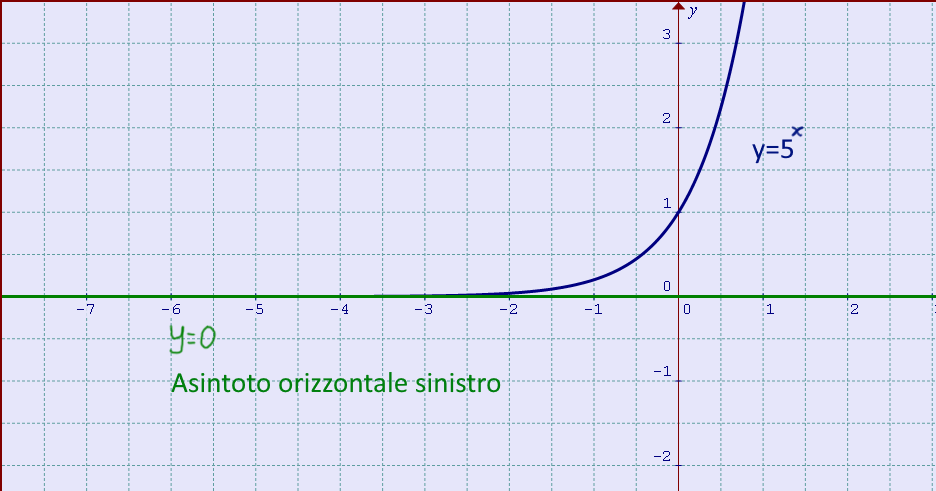
La seguente funzione esponenziale \( y = 5^x \)ha ad esempio un asintoto orizzontale sinistro. In particolare, l’asse \( x \) coincide con tale asintoto.
Condizioni sul dominio della funzione e legame con l’algoritmo di limite
Il fatto che il dominio della funzione debba essere illimitato (superiormente o inferiormente) è essenziale affinché la funzione possa ammettere almeno un asintoto orizzontale (destro o sinistro). Se considerassimo infatti come dominio della funzione un intervallo del tipo \( D_f = [a, \: b], \: a, \: b \in \mathbb{R} \), non avrebbe senso calcolare il limite per \( x \to \pm \infty \).
Osserviamo inoltre che una funzione definita in un intervallo illimitato sia superiormente, sia inferiormente, può avere due distinti asintoti orizzontali (dei quali uno destro e uno sinistro). Ciò corrisponde alla esistenza di entrambi i limiti:
\[ \lim_{x \to -\infty}f(x)=l_1, \quad l_1 \in \mathbb{R} \]
e
\[ \lim_{x \to +\infty}f(x)=l_2, \quad l_2 \in \mathbb{R} \]
con \( l_1 \neq l_2 \).
Un esempio di funzione avente due asintoti orizzontali è dato dalla funzione arcotangente, \( y = \arctan(x) \).
Guardiamo un po’ più da vicino questa funzione. Anzitutto, il suo dominio è illimitato, quindi ha senso chiedersi se essa ammette asintoti orizzontali.
Sappiamo poi dai “limiti fondamentali” che:
\[ \lim_{x \to -\infty}\arctan(x)=-\dfrac{\pi}{2}; \qquad \lim_{x \to +\infty}\arctan(x)=\dfrac{\pi}{2} \]
Tali condizioni rispecchiano infatti le definizioni appena date rispettivamente di asintoto orizzontale sinistro ed asintoto orizzontale destro.
Dunque, le rette \( y = -\dfrac{\pi}{2} \) e \( y = \dfrac{\pi}{2} \) sono entrambe asintoti orizzontali (rispettivamente sinitro e destro) per la funzione arcotangente.

Osserviamo che per \( x \to -\infty \) l’asintoto orizzontale destro approssima il grafico della funzione arcotangente.

La funzione viene cioè approssimata dall’asintoto in un intervallo del tipo \( ]k_\epsilon, \: +\infty[ \), con \( k_\epsilon \) sufficientemente grande. E’ chiaro infatti che se \( k_\epsilon \) non è abbastanza grande, la funzione nell’intorno \( ]k_\epsilon, \: +\infty[ \) non sarà approssimata dall’asintoto, come si può vedere dalla figura.
Riprendiamo allora la definizione di limite finito per x che tende a più infinito.
Affinché la funzione \( f(x) \) abbia per \( x \to +\infty \) limite pari ad \( l_2 \in \mathbb{R} \), cosa dovremo avere? Dovrà accadere che scelto comunque \( \epsilon > 0 \), la quantità \( |f(x)-l_2| \) in una qualunque \( x \) nell’intorno \( ]k_\epsilon, \: +\infty[ \) dovrà essere minore di \( \epsilon \).
Detta in altri termini, affinché \( y=l_2 \) sia asintoto orizzontale destro per \( f(x) \) pretendiamo che la differenza \( |f(x)-l_2| \) sia sempre minore di un \( \epsilon>0 \) piccolo quanto vogliamo, per tutte le \( x \in ]k_\epsilon, +\infty[ \).
E questo è ciò che effettivamente succede nell’algoritmo di limite finito per \( x \) che tende ad infinito. Comunque scegliamo un \( \epsilon > 0 \), riusciamo a determinare un \( k_\epsilon\) per cui \( |f(x)-l_2|<\epsilon \) per ogni \( x \) che vive in \( ]k_\epsilon, +\infty[ \), cioè per ogni \( x > k_\epsilon \), proprio come recita la definizione di limite.
E’ dunque chiaro che il grafico della funzione in corrispondenza delle immagini \( f(x) \) nell’intorno \( ]k_\epsilon, +\infty[ \) potrà essere confuso con l’asintoto orizzontale soltanto se \( k_\epsilon \) è infinitamente grande. Ma ciò avviene per certo se è rispettata la condizione di limite precedentemente indicata.
Allo stesso modo, osserviamo come per \( x \to -\infty \) l’asintoto orizzontale sinistro approssima il grafico della funzione arcotangente:
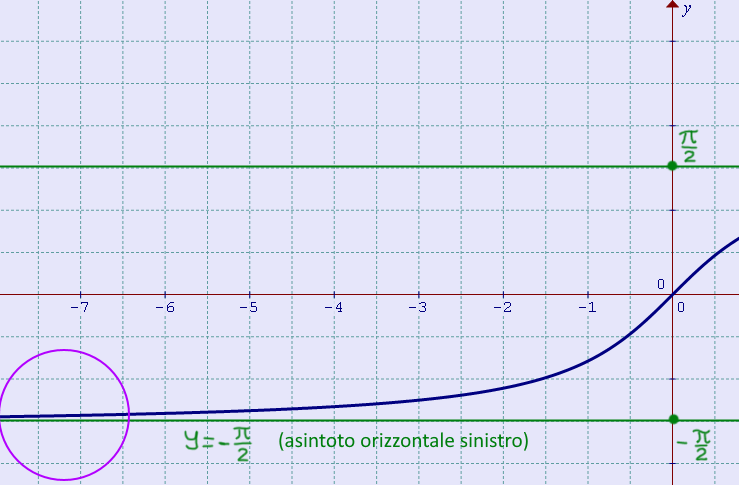
E’ infine utile osservare che affinché una funzione ammetta un asintoto orizzontale sinistro, è sufficiente che la funzione sia definita in un insieme limitato inferiormente. Allo stesso modo, affinché una funzione ammetta un asintoto orizzontale destro, è sufficiente che la funzione sia definita in un insieme illimitato superiormente. Non pretendiamo dunque per gli asintoti orizzontali destro e sinistro, a differenza di quanto richiesto per l’asintoto orizzontale bilatero, che la funzione sia necessariamente definita in un insieme illimitato sia superiormente, sia inferiormente .
Ad esempio, per una funzione definita in \( D_f = ]a, +\infty[, \: \:a \in \mathbb{R} \), ha perfettamente senso chiedersi se ammette un asintoto orizzontale destro, mentre non ha senso chiedersi se ammette un asintoto orizzontale sinistro. E ovviamente, non ammetterà sicuramente nemmeno asintoto orizzontale bilatero.
Esempi (ricerca di asintoti orizzontali)
Esempio 1
La funzione esponenziale \( y=5^x \) è definita in tutto \( \mathbb{R} \). Questo è, ovviamente, un intervallo illimitato. Dunque ha senso controllare se tale funzione ammette asintoti orizzontali sinistro e destro.
Riprendiamo le condizioni di limite nelle definizioni date per gli asintoti orizzontali.
Ricerchiamo l’asintoto orizzontale sinistro:
\[ \lim_{x \to -\infty}5^x =0\]
Il limite esiste finito per cui la retta \( y=0 \) è asintoto orizzontale sinistro per la funzione \( y=5^x \). Ritroviamo il risultato che già avevamo visto graficamente in precedenza.
Osserviamo però che:
\[ \lim_{x \to +\infty}5^x=+\infty \]
Il limite esiste ma non è finito, di conseguenza la funzione \( y=5^x \) non ammette asintoto orizzontale destro.
Esempio 2
Consideriamo la funzione:
\[ y=\dfrac{\sin x}{x} \]
Essa ha per dominio l’insieme \( D_f = ]-\infty, \: +\infty[ – \{0\} \), cioè tutti i reali escluso lo 0. Tale insieme di definizione è illimitato sia superiormente, sia inferiormente ed ha dunque senso ricercare entrambi gli asintoti orizzontali destro e sinistro.
Si ha in particolare:
\[ \lim_{x \to -\infty}\dfrac{\sin x}{x}=0 \]
e:
\[ \lim_{x \to +\infty}\dfrac{\sin x}{x}=0 \]
Tali limiti si calcolano osservando che la funzione \( \sin(x) \) è limitata, in quanto oscilla indefinitamente tra i valori \( -1 \) e \( 1 \). Tale oscillazione è trascurabile all’infinito e dunque i limiti possono essere visti come rapporto tra una quantità costante e una quantità infinita. Dall’algebra degli infiniti ed infinitesimi discendono dunque i risultati.
Osserviamo che i due limiti sono finiti e uguali tra loro. Possiamo pertanto affermare che la funzione ha un asintoto orizzontale bilatero dato dalla retta \( y=0 \).
Un tale asintoto riflette il comportamento di entrambi gli asintoti orizzontali destro e sinistro. Infatti, l’asintoto \( y=0 \) approssima il grafico della funzione \( y=\dfrac{\sin x}{x} \) sia in un intorno di \( -\infty \), sia in un intorno di \( +\infty \). Dal seguente grafico possiamo infatti vedere che la funzione si stabilizza confondendosi con l’asse delle \( x \) sia a sinistra (per \( x \to -\infty \)), sia a destra (per \( x \to +\infty \)).

E’ tra l’altro interessante osservare che il grafico della funzione ha punti di intersezione con l’asintoto:

In particolare, i punti di intersezione fra la funzione e il suo asintoto sono addirittura infiniti. Ciò smonta chiaramente una conclusione errata che potrebbe insinuarsi nella nostra mente per la quale una funzione non avrebbe mai punti di intersezione con i suoi asintoti.
ESEMPIO 3
Ricerchiamo eventuali asintoti orizzontali per la funzione:
\[ y=e^{\small {\dfrac{3+x}{1-x}}} \]
Osserviamo che la funzione è definita in \( D_f=\mathbb{R}-\{1\} \) poiché per \( x=1 \) si annulla il denominatore dell’esponente. La funzione è comunque definita in un insieme illimitato e ha senso chiedersi se la funzione ammette un asintoto orizzontale bilatero.
Proviamo quindi a calcolare i limiti:
\[ \lim_{x \to -\infty}e^{\small {\dfrac{3+x}{1-x}}};\qquad \lim_{x \to +\infty}e^{\small {\dfrac{3+x}{1-x}}} \]
Possiamo vedere l’espressione all’interno di ciascun limite come una funzione composta. In particolare, essa è data dalla funzione componente interna \( f(x)=\dfrac{3+x}{1-x} \) e dalla funzione componente esterna \( g(x)=e^x \).
Cominciamo col vedere se esiste l’asintoto orizzontale sinistro per la funzione.
Applichiamo il teorema della funzione composta. Siamo costretti a controllarne le ipotesi poiché non ci viene detto dall’esercizio che sono soddisfatte. Anzitutto vediamo il limite della funzione interna:
\[ l=\lim_{x \to -\infty}\dfrac{3+x}{1-x}=\lim_{x \to -\infty} \dfrac{x}{-x}=-1 \]
Il limite è stato calcolato isolando la parte principale degli infiniti a numeratore e denominatore.
Abbiamo che la funzione \( g(x)=e^x \) è definita in un intorno di \( l=-1 \), per cui sussistono le condizioni iniziali per poter applicare il teorema del limite della funzione composta. Sussiste anche la seconda ipotesi del teorema, poiché \( g(x) \) è anche continua in \( l \) (infatti \( e^{-1}=\dfrac{1}{e} \).
Poniamo quindi:
\[ t=f(x) \Rightarrow t =\dfrac{3+x}{1-x} \]
Ora, dato che esiste il:
\[ \lim_{t \to l}g(t)=\lim_{t \to -1}e^t=\dfrac{1}{e} \]
esso è il risultato cercato. Quindi:
\[ \lim_{x \to -\infty}e^{\small {\dfrac{3+x}{1-x}}}=\dfrac{1}{e} \]
Possiamo dunque affermare che la funzione assegnata soddisfa la condizione per l’asintoto orizzontale sinistro.
Procediamo ora controllando se la funzione ammette anche asintoto orizzontale destro. Si ha:
\[ \lim_{x \to +\infty} \dfrac{3+x}{1-x}=-1 \]
Otteniamo per la funzione componente interna lo stesso risultato precedente, di conseguenza possiamo direttamente concludere:
\[ \lim_{x \to +\infty}e^{\small {\dfrac{3+x}{1-x}}}=\dfrac{1}{e} \]
Quindi la funzione soddisfa anche la condizione per l’asintoto orizzontale destro. In particolare, notiamo che i due limiti relativi alle condizioni di esistenza degli asintoti orizzontali destro e sinistro coincidono. Pertanto, possiamo concludere dicendo che la funzione assegnata ammette asintoto orizzontale bilatero di equazione \( y=\dfrac{1}{e} \).

Qui finisce la lezione sugli asintoti orizzontali. Come nota finale osserviamo che come per gli asintoti verticali, anche per gli asintoti orizzontali le condizioni di limite nelle definizioni sono necessarie e sufficienti per l’esistenza degli asintoti.
In altre parole, se sappiamo ad esempio che \( \lim_{x \to +\infty}f(x) = k, \: k \in \mathbb{R} \), allora siamo certi che la funzione ammette almeno un asintoto orizzontale destro.
Nella prossima lezione tratteremo l’ultima tipologia rimasta: gli asintoti obliqui. E vedremo che le condizioni che verranno fornite, per essi, sui limiti, sono soltanto necessarie ma non sufficienti. In parole povere, tali condizioni che vedremo sono richieste per l’esistenza di tali asintoti, ma non bastano 😉
Ciao a tutti!
