Nella precedente lezione abbiamo visto i limiti di alcune funzioni elementari calcolati mediante la definizione di continuità di una funzione in un punto. Ora ci porremo invece l’obiettivo di calcolare particolari limiti di funzioni elementari in punti \( x_0 \) nei quali la funzione non è definita oppure, anche se in essi definita, non è continua. Inoltre, calcoleremo tali particolari limiti di funzioni elementari anche in corrispondenza degli estremi illimitati del dominio delle funzioni (ad esempio, per \( x \to +\infty \)).
Per esempio, data una funzione \( f(x) \) di tipo elementare, definita in un intorno chiuso \( [a, b] \) , ci proponiamo di calcolare i limiti:
\[ \lim_{x \to a^+}f(x); \qquad \lim_{x \to b^-} f(x) \]
In questo caso, i teoremi sulle funzioni continue non ci sono di aiuto. Infatti, nonostante la funzione sia definita negli estremi, in essi la funzione è continua rispettivamente soltanto da destra e da sinistra. Quindi, per nessuno dei due estremi esistono entrambi i limiti destro e sinistro della funzione.
E’ evidente inoltre che se una funzione non è definita in un punto, questa non sarà in esso nemmeno continua. Infatti, come sappiamo, condizione necessaria per la continuità di una funzione in un punto è che essa sia definita in tale punto. Quindi, se vogliamo calcolare il limite di una funzione elementare in un punto nel quale essa non è definita, ancora una volta la definizione di continuità non può aiutarci.
E non ultimo, nel caso volessimo valutare il:
\[ \lim_{x \to +\infty}3^x \]
cioè il limite di una funzione esponenziale con base 3 per \( x \) che tende a più infinito, non abbiamo per il momento alcuno strumento a disposizione. E’ intuitivo che il limite sia pari a \( +\infty \), ma sulla base di quale principio possiamo affermare questo?
Nasce dunque l’esigenza di uno strumento che ci consenta di orientarci in questi particolari limiti di funzioni elementari. Tale strumento è dato dai teoremi sulle funzioni monotone.
Nota
Per completezza ho scelto di riportare nel seguito queste nozioni anche se solitamente argomento di Analisi Matematica 1 (cioè di un corso universitario) e non di un programma delle scuole superiori. Chi è interessato soltanto ai risultati di questi particolari limiti di funzioni elementari può saltare la parte seguente ed andare direttamente in fondo alla lezione.
Teoremi sulle funzioni monotone
Prima di introdurre i teoremi, è opportuno introdurre alcune definizioni.
Maggioranti, minoranti, estremi superiore ed inferiore
Dato un insieme di numeri reali \( A \), si definisce maggiorante per l’insieme \( A \) un qualsiasi numero \( y\) che soddisfi la relazione \( y\geq x, \quad \forall \: x \: \in A \). Ad esempio, dato l’insieme \( A=\{5, 7, 40\} \), i numeri \( 50 \) e \( 60 \) sono entrambi esempi di maggioranti di \( A \).
Dato un insieme di numeri reali \( A \), si definisce minorante per l’insieme \( A \) un qualsiasi numero \( y \) che soddisfi la relazione \( y\leq x, \quad \forall \: x \: \in A \). Per esempio, dato l’insieme \( A=\{-10,1, 50\} \) i numeri \( -10, \: -30 \: – 55 \) sono ciascuno un minorante di \( A \).
Intervalli del tipo \( [a, \: b], \quad a, \: b \in \mathbb{R} \) ammettono sia maggioranti (tutti gli \( y \geq b\)) e minoranti (tutti gli \( y \leq a \)).
Invece, un intervallo del tipo \( ]-\infty, \: a] \) ha maggioranti ma non ha minoranti, poiché numeri più piccoli di \( -\infty \) non esistono 🙂
Allo stesso modo, un intervallo del tipo \( [a, \: +\infty[ \) avrà minoranti ma non avrà maggioranti, poiché numeri più grandi di \( +\infty \) non esistono.
Ora, le nozioni di maggiorante e minorante non ci servono un gran che di per sé, ma sono importanti per definire le nozioni di estremo superiore ed estremo inferiore (sup e inf) di una funzione 🙂
Considerato un intervallo avente maggioranti, l’estremo superiore è il più piccolo dei maggioranti.
Considerato un intervallo avente minoranti, l’estremo inferiore è il più grande dei minoranti.
In parole povere, dato l’intervallo \( [10, 50] \), il valore \( 10 \) è l’estremo inferiore di tale intervallo mentre \( 50 \) è l’estremo superiore.
E’ importante rilevare che essendo il sup e l’inf dei particolari maggioranti o minoranti, questi possono appartenere o non appartenere all’insieme. Di conseguenza, considerato l’intervallo aperto \( ]a, \: b[ \), avremo come estremo inferiore il valore \( a \) e come estremo superiore il valore \( b \), anche se \( a \) e \( b \) non appartengono all’intervallo.
Nel caso dell’intervallo chiuso \( [a, \: b] \), possiamo dire che \( a \), oltre ad essere l’estremo inferiore, è anche il minimo dell’intervallo e che \( b \) è il massimo (oltre che l’estremo superiore). Nel caso dell’aperto, invece, le definizioni di minimo e massimo, sebbene più intuitive, non funzionano (il massimo e il minimo devono appartenere all’insieme per definizione). Di conseguenza, vengono usati i concetti di estremo superiore ed inferiore, valevoli anche per intervalli aperti 🙂
Inoltre, gli estremi superiore ed inferiore “funzionano benissimo” anche in caso di intervalli illimitati (superiormente o inferiormente). Ad esempio, dato l’intervallo \( [a, +\infty[ \), il suo estremo superiore è \( +\infty \). Dato invece l’intervallo \( ]-\infty, \: b[ \), il suo estremo inferiore è \( -\infty \).
Funzioni monotone
Una funzione \( f(x) \) definita in \( D_f \) si dice crescente (non strettamente) in un intervallo \( I \subseteq D_f \)se presi due punti \( x_1, \: x_2 \in D_f \) con \( x_1 < x_2 \), risulta \( f(x_2)\geq f(x_1) \).
Una funzione \( f(x) \) definita in \( D_f \) si dice decrescente (non strettamente) in un intervallo \( I \subseteq D_f \)se presi due punti \( x_1, \: x_2 \in D_f \) con \( x_1 < x_2 \), risulta \( f(x_2)\leq f(x_1) \).
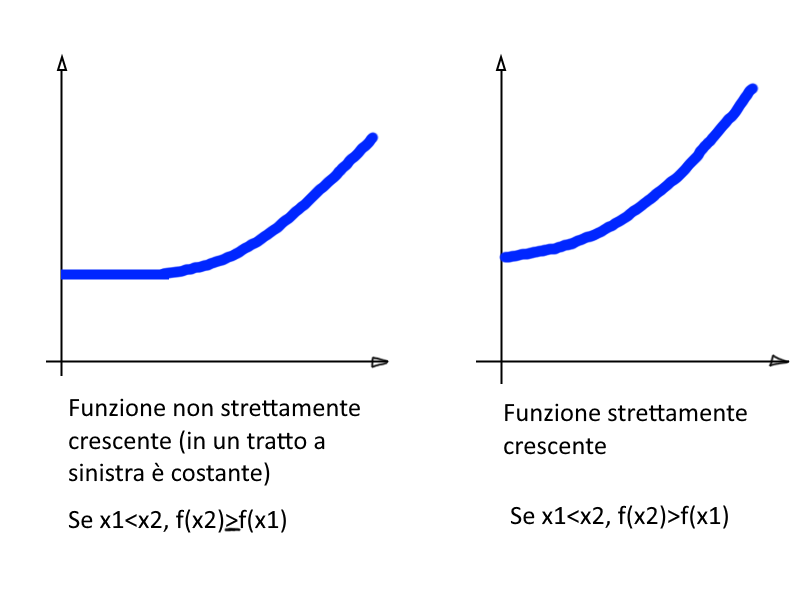
La disuguaglianze relative ad \( f(x) \) sono non strette (cioè, abbiamo le condizioni \( f(x_2)\geq f(x_1) \) e \( f(x_2)\leq f(x_1) \), col simbolo di minore-uguale). Ciò significa che nell’intervallo, la funzione potrà rispettivamente crescere e/o essere costante, descrescere e/o essere costante.
Ad esempio, la seguente figura mostra la differenza fra crescenza in senso stretto e in senso lato (cioè non stretto):
(Nota: per i nostri scopi le precedenti definizioni sono accettabili. In realtà, andrebbe fatta la distinzione fra funzioni crescenti, non crescenti, decrescenti e non decrescenti.)
Una funzione \( f(x) \)si dice monotona in un intervallo del suo dominio se in tale intervallo la funzione è sempre crescente (strettamente o non strettamente) oppure è sempre decrescente (strettamente o non strettamente).
Se una funzione è monotona in tutto il suo dominio, si dirà semplicemente monotona.
Consideriamo per chiarire le idee la seguente funzione:
Essa ha un comportamento differente nei vari intervalli. In particolare:
- in [a, b], la funzione è sempre strettamente crescente. Quindi diremo che in [a, b] è monotona, poiché ha lo stesso comportamento in tutto [a, b];
- nell’intervallo [b, c] la funzione è costante ed è dunque monotona in tale intervallo (mantiene lo stesso comportamento);
- in [a, c] la funzione è crescente in senso non stretto, poiché in un tratto è crescente e in un tratto è costante. Anche in [a, c] la funzione è monotona;
- in [c, d] la funzione è crescente in senso stretto e quindi monotona;
- nell’intervallo [d, e] la funzione è decrescente in senso stretto e quindi monotona (ancora, ha lo stesso comportamento in questo intervallo);
- in [d, f] la funzione è decrescente non strettamente poiché in un tratto decrescente e in un tratto costante. La funzione è comunque monotona in [d,f] poiché in tale intervallo è sempre non strettamente decrescente;
- nell’intervallo [c, e] la funzione NON è monotona, poiché in un tratto crescente e in un tratto decrescente;
- globalmente, cioè in tutto il suo dominio [a, f], la funzione NON è monotona poiché in alcuni intervalli del dominio è crescente e in altri decrescente.
Funzioni limitate e illimitate
Le seguenti definizioni sono importanti per poter successivamente applicare il teorema delle funzioni monotone per il calcolo dei limiti di funzioni elementari.
Una funzione \( f(x) \) definita in \( D_f \) e a valori in \( \mathbb{R} \)si dice limitata superiormente nel suo dominio se esiste un \( \quad M \in \mathbb{R} \) tale che risulti \( f(x)\leq M \) per ogni \( x \in D_f \).
Una funzione \( f(x) \) definita in \( D_f \) e a valori in \( \mathbb{R} \)si dice limitata inferiormente nel suo dominio se esiste un \( \quad M \in \mathbb{R} \) tale che risulti \( f(x)\geq M \) per ogni \( x \in D_f \).
Le funzioni che non rispettano tali condizioni sono invece illimitate superiormente e/o inferiormente.
Ora, tutte queste definizioni ci servono per introdurre lo strumento di cui abbiamo bisogno, cioè un mezzo per poter calcolare il limite di funzioni monotone in casi particolari. Se sappiamo ad esempio che una funzione elementare è monotona, anche soltanto in un intervallo, possiamo calcolare il limite per \( x \to \infty \) applicando il seguente teorema.
Teorema per il limite di una funzione monotona
Il teorema per il limite di una funzione monotona è uno strumento che ci consente di calcolare il limite di funzioni monotone in casi particolari:
- funzione monotona in un intervallo aperto \( ]a, b[ \): è possibile calcolare il limite della funzione per \( x \) che tende a ciascun estremo, pur non essendo compreso nel dominio;
- funzione monotona in intervalli del tipo \( ]M, +\infty[ \) e \( ]-\infty, -M[ \) (con \( M \in \mathbb{R} \: \text{e} \: M> 0 \): è possibile calcolare il limite sia per x che tende ad un estremo illimitato (più o meno infinito), sia per x che tende all’estremo finito M.
Enunciamo il teorema nei vari casi. Ricordiamo che per semplicità adottiamo le definizioni di funzione crescente e decrescente come nei precedenti richiami 😉 In questo modo secondo me è più semplice capire i concetti. Sta poi a voi regolarvi in base a quanto richiesto nel vostro corso di studi.
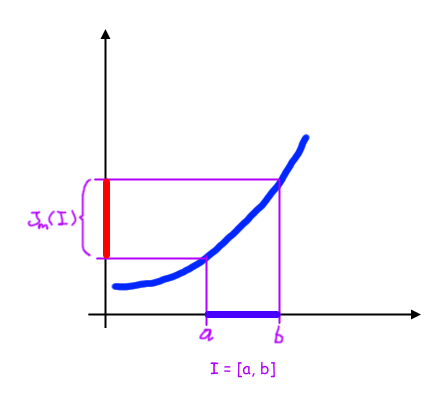
Premettiamo anche che con la scrittura:
\[ \sup_{x \in I}f(x) \]
intendiamo l’estremo superiore determinato considerando i valori di \( f(x) \) calcolati per tutti gli \( x \) appartenenti all’intervallo \( I \).
Detta in altri termini, con tale scrittura indichiamo l’estremo superiore dell’insieme \( \Im(I) \), cioè dell’immagine della funzione relativa all’intervallo \( I \). Consideriamo cioè soltanto una parte dell’immagine \( \Im(D_f) \) della funzione, cioè l’immagine ottenuta con i valori \( x \in I\subseteq D_f \), e valutiamo l’estremo superiore di tale immagine 🙂
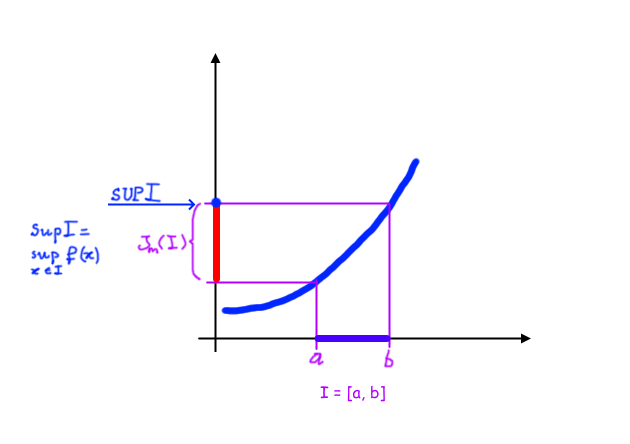
Come ultima nota, è piuttosto “ghiotto” introdurre a questo punto una definizione alternativa per le funzioni limitate, che ci sarà utilissima per applicare meglio il teorema 😉
Diremo che una funzione \( f(x) \) definita in \( D_f \subseteq \mathbb{R} \) è illimitata superiormente (inferiormente) se l’estremo superiore (inferiore) dell’immagine di \( f(x) \) è \( +\infty \) (\( -\infty \)).
Tali definizioni, apparentemente ostiche, dovrebbero risultare chiare osservando il seguente disegno 🙂
Analogo discorso sarà valevole per l’estremo inferiore.
Primo caso: intorno \( ]a, \: b[ \).
Si abbia una funzione \( f(x) \) avente dominio \( D_f \subseteq \mathbb{R} \) e a valori reali. Consideriamo un intervallo \( ]a, b[ \subseteq D_f \) nel quale la funzione è definita. Sia la funzione \( f(x) \) monotona nell’intervallo \( ]a, \: b[ \).
Sotto queste ipotesi, se \( f(x) \) risulta crescente (anche non strettamente) in \( ]a, \: b[ \), si ha che:
\[ \lim_{x \to a^+}f(x)=\inf_{x \in ]a,b[}f(x) \]
\[ \lim_{x \to b^-}f(x)=\sup_{x \in ]a,b[}f(x) \]
Invece, se \( f(x) \) risulta decrescente (anche non strettamente) in \( ]a, \: b[ \) si ha:
\[ \lim_{x \to a^+}f(x)=\sup_{x \in ]a,b[}f(x) \]
\[ \lim_{x \to b^-}f(x)=\inf_{x \in ]a,b[}f(x) \]
Secondo caso: intorno \( ]-\infty, \: M[ \).
Si abbia una funzione \( f(x) \) avente dominio \( D_f \subseteq \mathbb{R} \) e a valori reali. Consideriamo un intervallo \( ]-\infty, -M[ \subseteq D_f \) con \( M>0 \) nel quale la funzione è definita. Sia la funzione \( f(x) \) monotona nell’intervallo \( ]-\infty, -M[ \).
Sotto dette ipotesi, se le funzione è crescente (anche non strettamente) nell’intervallo \( ]-\infty, -M[ \) si ha:
\[ \lim_{x \to -\infty}f(x)=\inf_{x \in ]-\infty, -M[}f(x) \]
\[ \lim_{x \to -M^-}f(x)=\sup_{x \in ]-\infty, -M[}f(x) \]
Se invece la funzione è descrescente (anche non strettamente) in \( ]-\infty, -M[ \), si ha:
\[ \lim_{x \to -\infty}f(x)=\sup_{x \in ]-\infty, -M[}f(x) \]
\[ \lim_{x \to -M^-}f(x)=\inf_{x \in ]-\infty, -M[}f(x) \]
Terzo caso: intorno \( ]M, \: +\infty[ \).
Si abbia una funzione \( f(x) \) avente dominio \( D_f \subseteq \mathbb{R} \) e a valori reali. Consideriamo un intervallo \( ]M, +\infty[ \subseteq D_f \) con \( M>0 \) nel quale la funzione è definita. Sia la funzione \( f(x) \) monotona nell’intervallo \( ]M, +\infty[ \).
Sotto dette ipotesi, se le funzione è crescente (anche non strettamente) nell’intervallo \(]M, +\infty[ \) si ha:
\[ \lim_{x \to \infty}f(x)=\sup_{x \in ]M, +\infty[}f(x) \]
\[ \lim_{x \to M^+}f(x)=\inf_{x \in ]M, +\infty[}f(x) \]
Se invece la funzione è descrescente (anche non strettamente) in \( ]M, +\infty[ \), si ha:
\[ \lim_{x \to \infty}f(x)=\inf_{x \in]M, +\infty[ }f(x) \]
\[ \lim_{x \to M^+}f(x)=\sup_{x \in ]M, +\infty[ }f(x) \]
Applicazione del teorema delle funzioni monotone per il calcolo dei limiti delle funzioni elementari
Supponiamo di dover calcolare:
\[ \lim_{x \to +\infty} x^2 \]
Non possiamo risolvere il limite per sostituzione diretta poiché evidentemente la \( x \) non tende ad un valore finito.
Osserviamo che la funzione \( f(x)=x^2 \) è monotona nell’intervallo \( [0, +\infty[ \).
Inoltre, in tale intervallo la funzione non è limitata superiormente. Infatti, per ogni valore di \( f(x_0)=x_0^2 \) esiste sempre un numero \( M\in\mathbb{R} \) tale che \( M>f(x_0) \) (tenete presente quanto detto nel paragrafo sulle funzioni limitate 😉 ).
Se dunque la funzione è illimitata superiormente nell’intervallo, succederà che prendendo un \( x \) “sempre più grande” otterremo un valore \( f(x) \)sempre più grande. Detta in linguaggio matematico, avremo cioè che l’estremo superiore dell’immagine dell’intervallo \( [0, +\infty[ \) sarà proprio \( +\infty \). Dunque, applicando il teorema delle funzioni monotone potremo dire che:
\[ \lim_{x \to +\infty}x^2= \sup_{[0, +\infty[}x^2=+\infty \]
Ora, non staremo qui ad applicare questi ragionamenti per tutte le funzioni elementari. Riportiamo a seguire solamente i risultati di tali ragionamenti. L’esempio appena mostrato è però importante per capire come si applica il teorema delle funzioni monotone.
Particolari limiti di funzioni elementari (con il teorema delle funzioni monotone)
Ora vi presento il premio che otteniamo grazie alla lettura dei precedenti paragrafi (o anche grazie alla non lettura degli stessi per chi li ha saltati :P). In pratica, siamo ora in grado di estendere ciò che sappiamo per le funzioni elementari, in quanto grazie al teorema delle funzioni monotone possiamo valutare il limite di tali funzioni anche negli estremi illimitati e in punti ove esse non sono definite o comunque non sono continue 🙂 Nella pratica è conveniente ricordarsi a memoria i seguenti limiti o comunque essere in grado di ricavarli ragionando con il grafico della funzione della quale si vuole calcolare il limite.
Ecco dunque un elenco dei principali limiti particolari di funzioni elementari (indicati a volte come limiti fondamentali).
Funzione costante
Per la funzione costante, cioè \( y=k, \qquad k \in \mathbb{R} \), abbiamo i limiti:
\[ \lim_{x \to -\infty}k = k; \qquad \lim_{x \to +\infty}k = k \]
Funzione identità
Per la funzione identità, cioè \( y=x, \quad x \in \mathbb{R} \), abbiamo i limiti:
\[ \lim_{x \to -\infty}x=-\infty; \qquad \lim_{x \to +\infty}x=+\infty; \]
Funzione potenza
Per la funzione potenza, cioè \( y=x^p, \qquad p \in \mathbb{N}, \quad p>1 \), valgono i limiti:
\[ \lim_{x \to -\infty}x^p=+\infty \qquad \text{se p è pari} \]
\[ \lim_{x \to -\infty}x^p=-\infty \qquad \text{se p è dispari} \]
e infine:
\[ \lim_{x \to +\infty} x^p=+\infty \quad \forall \: p \: \in \mathbb{N} \]
Funzione esponenziale
Per la funzione esponenziale, cioè \( y = a^x , \qquad 0<a<1 \quad\vee \quad a > 1 \) valgono i limiti:
\[ \lim_{x \to +\infty}a^x = +\infty \quad \text{per a > 1} \]
\[ \lim_{x \to +\infty} a^x=0 \quad \text{per 0<a<1} \]
\[ \lim_{x \to -\infty}a^x=0 \quad \text{per a > 1} \]
\[ \lim_{x \to -\infty}a^x=+\infty \quad \text{per 0<a<1} \]
Funzione radice quadrata
Per la funzione radice quadrata \( y = \sqrt{x} \) vale il limite:
\[ \lim_{x \to +\infty}\sqrt{x}=+\infty \]
Il risultato si estende a tutte le funzioni radice con indice \( n \) pari:
\[ \lim_{x \to +\infty}\sqrt[n]{x}=+\infty, \qquad n \: \text{pari} \]
Poiché le funzioni radice con indice pari sono definite solo nei reali positivi (compreso lo zero), non ha senso valutare il limite per \( x \) che tende a \( -\infty \).
Funzione radice cubica
Per la funzione radice cubica, ovvero \( y=\sqrt[3]{x} \), definita in tutti i reali, valgono i limiti:
\[ \lim_{x \to -\infty}\sqrt[3]{x}=-\infty; \qquad \lim_{x \to +\infty}\sqrt[3]{x}=+\infty \]
Il risultato si estende a tutte le funzioni radice con indice dispari:
\[ \lim_{x \to -\infty}\sqrt[n]{x}=-\infty; \qquad \lim_{x \to +\infty}\sqrt[n]{x}=+\infty; \qquad n \:\:\text{dispari} \]
Funzione segno
La funzione segno, \( y=\mbox{sgn}(x) \), è definita in tutti i reali escluso lo zero. Esso è dunque punto di discontinuità per la funzione. Tuttavia, grazie ai teoremi sulle funzioni monotone possiamo scrivere:
\[ \lim_{x \to 0^-}\mbox{sgn}(x)=-1; \qquad \lim_{x \to 0^+}\mbox{sgn}(x)=1 \]
Funzione valore assoluto
Per la funzione valore assoluto, ovvero \( y=|x| \), possiamo scrivere:
\[ \lim_{x \to -\infty}|x|=+\infty; \qquad \lim_{x \to +\infty}|x|=+\infty \]
Funzione logaritmo
La funzione logaritmo è sempre definita nell’intorno \( ]0, +\infty[ \), a prescindere dalla base.
Il teorema delle funzioni monotone consente di valutare il limite della funzione logaritmo agli estremi dell’intervallo di definizione.
caso base maggiore di 1
\[ \lim_{x \to 0^+}\log_{a}x=-\infty; \qquad \lim_{x \to +\infty}\log_{a}x=+\infty; \qquad a>1 \]
caso base compresa fra 0 e 1
\[ \lim_{x \to 0^+}\log_{a}x=+\infty; \qquad \lim_{x \to +\infty}\log_{a}x=-\infty; \qquad 0<a<1 \]
Principali funzioni trigonometriche
Aggiungiamo ora al nostro bagaglio su particolari limiti delle funzioni elementari qualche informazione riguardante le funzioni trigonometriche.
Per le funzioni seno e coseno di \( x \) il teorema delle funzioni monotone non fornisce alcun aiuto per la determinazione dei relativi limiti per \( x \to +\infty \) (o meno infinito). Tuttavia, è possibile dimostrare che i seguenti limiti non esistono:
\[ \nexists \lim_{x \to +\infty}\cos(x); \qquad \nexists \lim_{x \to +\infty}\sin(x) \]
\[ \nexists \lim_{x \to -\infty}\cos(x); \qquad \nexists \lim_{x \to -\infty}\sin(x) \]
E’ comunque molto importante per gli esercizi ricordare che queste funzioni sono limitate, ovvero sempre comprese fra \( y=-1 \) e \( y=1 \). Capiterà infatti di avere funzioni non elementari nelle quali è presente un termine in seno e coseno, e tale limitatezza sarà una informazione importante per risolvere gli esercizi.
Per le funzioni tangente e cotangente ha qui senso valutare i limiti nei punti di discontinuità. In particolare abbiamo:
\[ \lim_{x \to \pi/2^+}\tan(x)=-\infty; \qquad \lim_{x \to \pi/2^-}\tan(x)=+\infty \]
\[ \lim_{x \to \pi^-}\cot(x)=-\infty_; \qquad \lim_{x \to \pi^+}\cot(x)=+\infty \]
Per quanto riguarda le funzioni trigonometriche inverse, applichiamo il teorema di monotonia delle funzioni agli estremi del loro dominio. In particolare otteniamo:
\[ \text{funzione arcoseno:} \qquad \lim_{x \to -1^+}\arcsin(x)=-\dfrac{\pi}{2}; \qquad \lim_{x \to 1^-}\arcsin(x)=\dfrac{\pi}{2} \]
\[ \text{funzione arcocoseno:} \qquad \lim_{x \to -1^+}\arccos(x)=\pi; \qquad \lim_{x \to 1^-}\arccos(x)=0 \]
\[ \text{funzione arcotangente: } \qquad \lim_{x \to -\infty}\arctan(x)=-\dfrac{\pi}{2}; \qquad \lim_{x \to \infty}\arctan(x)=\dfrac{\pi}{2}; \]
Abbiamo dunque visto alcuni particolari limiti di funzioni elementari (o limiti fondamentali) ottenuti con l’ausilio dei teoremi delle funzioni monotone. Questa lunga lezione finisce qui 🙂 Nella prossima vedremo le operazioni fra limiti.
Ciao a tutti! 🙂