In particolare, come intervengono i limiti destro e sinistro nella definizione di continuità di una funzione?
Sappiamo che per poter dire che una funzione ha in un punto \( x_0 \)un certo limite \( l \), la funzione dovrà ammettere per \( x_0 \)un limite uguale proprio a quel valore \( l \) sia per \( x \) che tende ad \( x_0 \) da destra, sia per \( x \) che tende ad \( x_0 \) da sinistra.
Viceversa, sappiamo anche che se una funzione ammette in un punto \( x_0 \) limite destro e sinistro entrambi uguali a \( l \), allora si avrà che \( lim_{x \to x_0}f(x)=l \).
Sinteticamente:
\[ \lim_{x \to x_0} f(x) = l \iff \lim_{x \to x_0^+} f(x) = \lim_{x \to x_0^-} f(x) = l \]
Ora, possiamo applicare questo risultato al concetto di continuità di una funzione?
In altre parole, possiamo dire che se \( \lim_{x \to x_0^+}f(x)=\lim_{x \to x_0^-}f(x)=f(x_0) \), allora \( \lim_{x \to x_0}f(x)=f(x_0) \)? La risposta è senz’altro affermativa 🙂
Quindi, se i due limiti destro e sinistro indicati esistono e sono uguali entrambi al valore \( l=f(x_0) \), allora la funzione sarà continua nel punto \( x_0 \).
Ora, cosa hanno di particolare i due limiti destro e sinistro che abbiamo appena scritto? Essi esprimono le definizioni di continuità a destra e a sinistra di una funzione in un punto 🙂
Continuità di una funzione: limiti destro e sinistro
Definizione (continuità a destra di una funzione in un punto)
Una funzione \( f(x) \) definita in \( D_f \in \mathbb{R} \), con \( x_0 \in D_f \) punto di accumulazione per \( D_f \), si dirà continua a destra nel punto \( x_0 \) se:
\[ \lim_{x \to x_0^+}f(x)=f(x_0) \]
Ovvero, una funzione si dirà continua a destra nel punto \( x_0 \)se il limite destro di tale funzione per \( x \to x_0^+ \) coincide con il valore assunto dalla funzione in \( x_0 \).
Definizione (continuità a sinistra di una funzione in un punto)
Una funzione \( f(x) \) definita in \( D_f \in \mathbb{R} \), con \( x_0 \in D_f \) punto di accumulazione per \( D_f \), si dirà continua a sinistra nel punto \( x_0 \) se:
\[ \lim_{x \to x_0^-}f(x)=f(x_0) \]
Ovvero, una funzione si dirà continua a sinistra nel punto \( x_0 \)se il limite sinistro di tale funzione per \( x \to x_0^-\) coincide con il valore assunto dalla funzione in \( x_0 \).
Osserviamo ancora una volta come le definizioni di limite destro e sinistro siano state adattate al concetto di continuità. Infatti, ora il punto \( x_0 \) deve sempre appartenere al dominio della funzione. Troviamo infatti nelle definizioni: \( x_0 \in D_f \).
Ora non ci resta che formalizzare la definizione di funzione continua utilizzando i limiti destro e sinistro 🙂
Definizione di funzione continua in un punto (con i limiti destro e sinistro)
Una funzione \( f(x) \), definita in \( D_f \in \mathbb{R} \), con \( x_0 \in D_f \) e \( x_0 \) punto di accumulazione per \( D_f \), si dice continua in \( x_0 \) se essa è continua sia a destra di \( x_0 \), sia a sinistra di \( x_0 \), ovvero:
\[ \lim_{x \to x_0} f(x) = f(x_0) \iff \lim_{x \to x_0^+}f(x) = \lim_{x \to x_0^-}f(x)= f(x_0) \]
Ovviamente, questa definizione può essere estesa banalmente al caso di una funzione continua in un intervallo e al caso di funzione continua (cioè una funzione continua in tutto il suo dominio). Più interessante è invece soffermarci al caso che segue.
Continuità agli estremi dell’intervallo di definizione di una funzione
Consideriamo una funzione \( f(x) \) definita in un intervallo \( [a, \: b] \subset \mathbb{R} \) , cioè un intervallo chiuso (comprende gli estremi) e reale (tutti i suoi elementi sono reali).
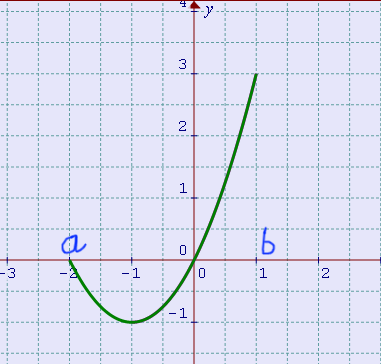
Cosa succede se proviamo a studiare la continuità della funzione negli estremi \( a \) e \( b \) dell’intervallo? Ci rendiamo conto che nasce la necessità di adattare la definizione di continuità al caso degli estremi.
Infatti, se usassimo la definizione di continuità così come la conosciamo ora, diremmo che la funzione non è continua agli estremi. Non è una sorpresa: nella definizione di continuità si richiede che il punto \( x_0 \) debba essere un punto di accumulazione per il dominio di \( f(x) \).
Ma, \( a \) non è per \( [a, b] \) un punto di accumulazione, poiché non esiste alcun intervallo simmetrico di \( a \) i cui punti appartengano tutti al dominio \( [a, b] \). Stesso discorso vale per \( b \), a conferma che non avremmo continuità per la funzione agli estremi del suo dominio – per come conosciamo la continuità ora ;).
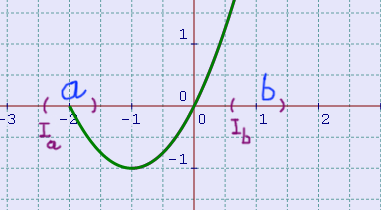
Tuttavia, possiamo chiederci se abbiamo continuità a destra e a sinistra per la funzione negli estremi. E, per definizione, diciamo che una funzione è continua nell’estremo \( a \) se in esso la funzione è continua a destra. Analogamente, diciamo che una funzione è continua nell’estremo \( b \) se in esso la funzione è continua a sinistra.
In particolare, abbiamo continuità per \( f(x) \) all’estremo \( a \) se:
\[ \lim_{x \to a^+}f(x)=f(a) \]
e abbiamo continuità per \( f(x) \) all’estremo \( b \) se:
\[ \lim_{x \to b^-}f(x) = f(b) \]
In questa lezione abbiamo dunque visto la relazione tra limiti destro e sinistro e continuità. Nella prossima lezione vedremo invece in quali casi non si ha la continuità e tratteremo il concetto di punti di discontinuità per una funzione.
Ciao! 🙂
