Per stabilire le regole per il calcolo degli integrali fondamentali non useremo i limiti così come invece abbiamo fatto per le derivate fondamentali. Piuttosto, per ricavare le regole di integrazione delle funzioni elementari cercheremo in ciascun caso di tradurre le regole di calcolo delle derivate al caso degli integrali fondamentali, ragionando sulla definizione di antiderivata.
Vediamo allora subito gli integrali fondamentali, ovvero le principali regole per il calcolo degli integrali indefiniti delle funzioni elementari e comunque di quegli integrali che discendono dalle derivate fondamentali. 🙂
Integrali fondamentali (come integrare le funzioni elementari)
Per il calcolo degli integrali fondamentali dobbiamo tenere conto della definizione di antiderivata. Un’antiderivata (o primitiva) per la funzione \( f(x) \) è una funzione \( F(x) \) tale che:
\[ \dfrac{d}{dx}F(x)=f(x) \]
ovvero una funzione \( F(x) \) che, se derivata, restituisce la funzione \( f(x) \).
Così, per stabilire le regole di integrazione per il calcolo degli integrali indefiniti dovremo basarci proprio sul fatto di dover riottenere, a partire da una qualsiasi antiderivata \( F(x) \) di \( f(x) \), la funzione \( f(x) \) stessa.
Ricordiamo che se una funzione \( f(x) \) è integrabile, le sue primitive o antiderivate sono infinite e tutte della forma \( F(x)+c \):
\[ \int f(x) \, dx = F(x)+c, \qquad c \in \mathbb{R} \]
Il risultato dell’operazione di integrale indefinito restituisce quindi una famiglia di antiderivate o primitive.
I passi da seguire per stabilire le regole per il calcolo degli integrali fondamentali sono per quanto detto i seguenti:
- ricercare una funzione \( F(x) \) che, una volta derivata, restituisca la funzione di partenza \( f(x) \);
- cercare di capire con quale regola si può ricavare un’antiderivata \( F(x) \) a partire dalla funzione \( f(x) \) da integrare.
Ovviamente tali regole andranno stabilite una volta per tutte e quindi imparate a memoria, in modo da poter calcolare gli integrali indefiniti a colpo sicuro. 😉
Passiamo allora in rassegna alcune funzioni elementari e vediamo di definire le regole per il calcolo dei corrispondenti integrali fondamentali in ciascun caso. A seguire è inoltre disponibile una tabella degli integrali fondamentali.
Integrale fondamentale della funzione costante
Consideriamo l’integrale indefinito:
\[ \int a \, dx \]
ove \( a \) è una costante reale, ovvero \( a \in \mathbb{R} \).
In questo caso la funzione di partenza (funzione integranda, funzione da integrare) è la funzione costante \( f(x)=a \).
Dalle regole di derivazione relative alle derivate fondamentali, è immediato ricordare che:
\[ \dfrac{d}{dx}ax = a \]
Di conseguenza, se prendiamo \( F(x)=ax \) calcolandone la derivata otteniamo la funzione di partenza \( f(x)=a \). Quindi \( F(x) \) è un’antiderivata per \( f(x) \).
Infine, poiché le antiderivate di una qualunque funzione integrabile sono infinite, scriviamo in conclusione:
\[ \boxed{\int a \, dx = ax+c, \qquad c \in \mathbb{R}} \]
e questa è la regola di integrazione per la funzione costante. 😉
Ricordiamo ancora una volta che l’aver aggiunto la costante \( c \) si giustifica osservando che la derivata di una costante è nulla, per cui qualunque funzione della forma \( F(x)+c \) è un’antiderivata per \( f(x) \). La costante \( c \) può essere un numero reale qualunque.
Integrale di una funzione potenza
Ci proponiamo ora di calcolare l’integrale indefinito:
\[ \int x^n \, dx, \qquad n \in \mathbb{R} \]
ove la funzione integranda \( f(x)=x^n \) è la funzione potenza.
Dalle derivate fondamentali abbiamo:
\[ \dfrac{d}{dx}x^n = n \cdot x^{n-1} \]
da cui è chiaro che un’antiderivata di \( n x ^{n-1} \) è pari a \( x^n \):
\[ f(x) = n x ^{n-1} \quad \Rightarrow \quad F(x) = x^n \]
Ora, per passare da \( f(x) \) ad \( F(x) \) dobbiamo dividere l’espressione di \( f(x) \) per \( n \) e sommare \( 1 \) all’esponente della \( x \).
E’ importante osservare che se aggiungiamo \( 1 \) all’esponente \( n-1 \) otteniamo proprio \( n \). Così in modo del tutto equivalente quello che dobbiamo fare nella funzione di partenza è sommare \( 1 \) all’esponente e inoltre dividere per l’esponente così ottenuto.
Ora, la funzione \( f(x) \) è qui della forma \( n x ^ {n-1} \) ma le considerazioni fatte valgono per una funzione potenza nella forma generale.
In conclusione, poiché le antiderivate per \( f(x) \) sono infinite possiamo scrivere:
\[ \boxed{\int x^n \, dx = \dfrac{1}{n+1}x^{n+1}+c, \qquad c \in \mathbb{R}, \quad n \neq -1} \]
Abbiamo così stabilito la regola per il calcolo dell’integrale fondamentale della funzione potenza.
La regola appena scritta è valida soltanto per esponenti diversi da \( -1 \). Infatti per \( n = -1 \) la frazione algebrica \( \dfrac{1}{n+1} \) perde di significato (si annulla il denominatore).
Basta tuttavia ricordare che:
\[ \dfrac{d}{dx}\log x = \dfrac{1}{x} \]
Osserviamo che \( \dfrac{1}{x}=x^{-1} \). Per cui ci ritroviamo a ragionare proprio nel caso di esponente \( n = -1 \).
Di conseguenza, per \( x > 0 \) possiamo affermare che \( \log x \) è un’antiderivata per \( f(x)=\dfrac{1}{x} \).
Per \( x < 0 \) la funzione \( \log x \) non è definita per cui dovremo considerare il valore assoluto dell’argomento del logaritmo. In generale allora avremo la seguente regola di integrazione:
\[ \int x^{-1} \, dx = \log |x|+c \]
o equivalentemente:
\[ \boxed{\int \dfrac{1}{x} \, dx = \log |x|+c} \]
E’ infine importante osservare che funzioni elementari costituite da radicali possono essere ricondotte a potenze con esponente fratto e quindi integrate ancora seguendo la regola dell’integrale fondamentale della funzione potenza. Ad esempio:
\[ \small \int \sqrt[3]{x^5 }\, dx = \int x^{\frac{5}{3}} \, dx = \dfrac{1}{\dfrac{5}{3}+1}\cdot x ^{\frac{5}{3}+1}=\dfrac{1}{\dfrac{8}{3}}\cdot x^{\frac{8}{3}}= \dfrac{3}{8} \cdot x^\frac{8}{3}=\dfrac{3}{8}\sqrt[3]{x^8}+c, \quad c \in \mathbb{R} \]
Il risultato può essere ulteriormente semplificato portando fuori dalla radice un fattore \( x^2 \):
\[ \int \sqrt[3]{x^5 }\, dx = \dfrac{3}{8}x^2\sqrt[3]{x^2}+c, \quad c \in \mathbb{R} \]
Integrale fondamentale della funzione seno
Vediamo come integrare la funzione elementare \( f(x)=\sin x \), ovvero calcolare l’integrale indefinito:
\[ \int \sin x \, dx \]
Per le derivate fondamentali abbiamo:
\[ \dfrac{d}{dx}\cos x = -\sin x \]
Osserviamo che ci ritroviamo un segno meno, per cui in base a quanto scritto possiamo soltanto affermare che \( F(x)=\cos x \) è un’antiderivata per \( f(x) = -\sin x \). Tuttavia, moltiplicando ambo i membri della precedente relazione per \( -1 \):
\[ -1 \cdot \dfrac{d}{dx}\cos x = -1 \cdot (-\sin x) \]
ovvero:
\[ \dfrac{d}{dx}\left(-\cos x \right) = \sin x \]
Di conseguenza, un’antiderivata per la funzione \( f(x)=\sin x \) è \( F(x)=-\cos x \). Infine, per il calcolo dell’integrale indefinito di partenza otteniamo:
\[ \boxed{\int \sin x \, dx = -\cos x +c, \qquad c \in \mathbb{R}} \]
Integrale fondamentale della funzione coseno
Per il calcolo dell’integrale indefinito della funzione coseno procediamo in modo del tutto simile al caso precedente. Poiché
\[ \dfrac{d}{dx}\sin x = \cos x \]
si ha:
\[ f(x) = \cos x \quad \Rightarrow \quad F(x)=\sin x \]
ovvero \( F(x) = \sin x \) è un’antiderivata per \( f(x) = \cos x \).
Otteniamo così:
\[ \boxed{\int \cos x \, dx = \sin x+c, \qquad c \in \mathbb{R}} \]
NOTA: è importante confrontare tra loro le derivate e gli integrali fondamentali delle funzioni seno e coseno, in modo da stabilire una regola mnemonica che consenta di ricordare più facilmente le corrispondenti regole di calcolo. In particolare:
\[ \dfrac{d}{dx}\sin x = \cos x; \qquad \int \sin x = -\cos x+c \]
e inoltre:
\[ \dfrac{d}{dx}\cos x = -\sin x; \qquad \int \cos x \, dx = \sin x +c, \qquad c \in \mathbb{R} \]
Di conseguenza, i risultati oltre che per la presenza della costante additiva differiscono soltanto per un segno. Così, in termini informali, se la derivata della funzione seno è il coseno (con segno più), un’antiderivata della funzione seno è data da meno coseno. Allo stesso modo, se la derivata della funzione coseno è data da meno seno, un’antiderivata della funzione coseno è data dalla funzione seno (con segno più). Con questa osservazione se ricordiamo le derivate fondamentali delle funzioni seno e coseno possiamo ricavare immediatamente i corrispondenti integrali indefiniti. 😉
Tabella degli integrali fondamentali
Forniamo a seguire una tabella che riporta tutti i principali integrali fondamentali. I ragionamenti con i quali sono state ricavate tutte le regole a seguire sono perfettamente simili a quelli adottati per stabilire le regole sin qui presentate.
Tabella degli integrali fondamentali
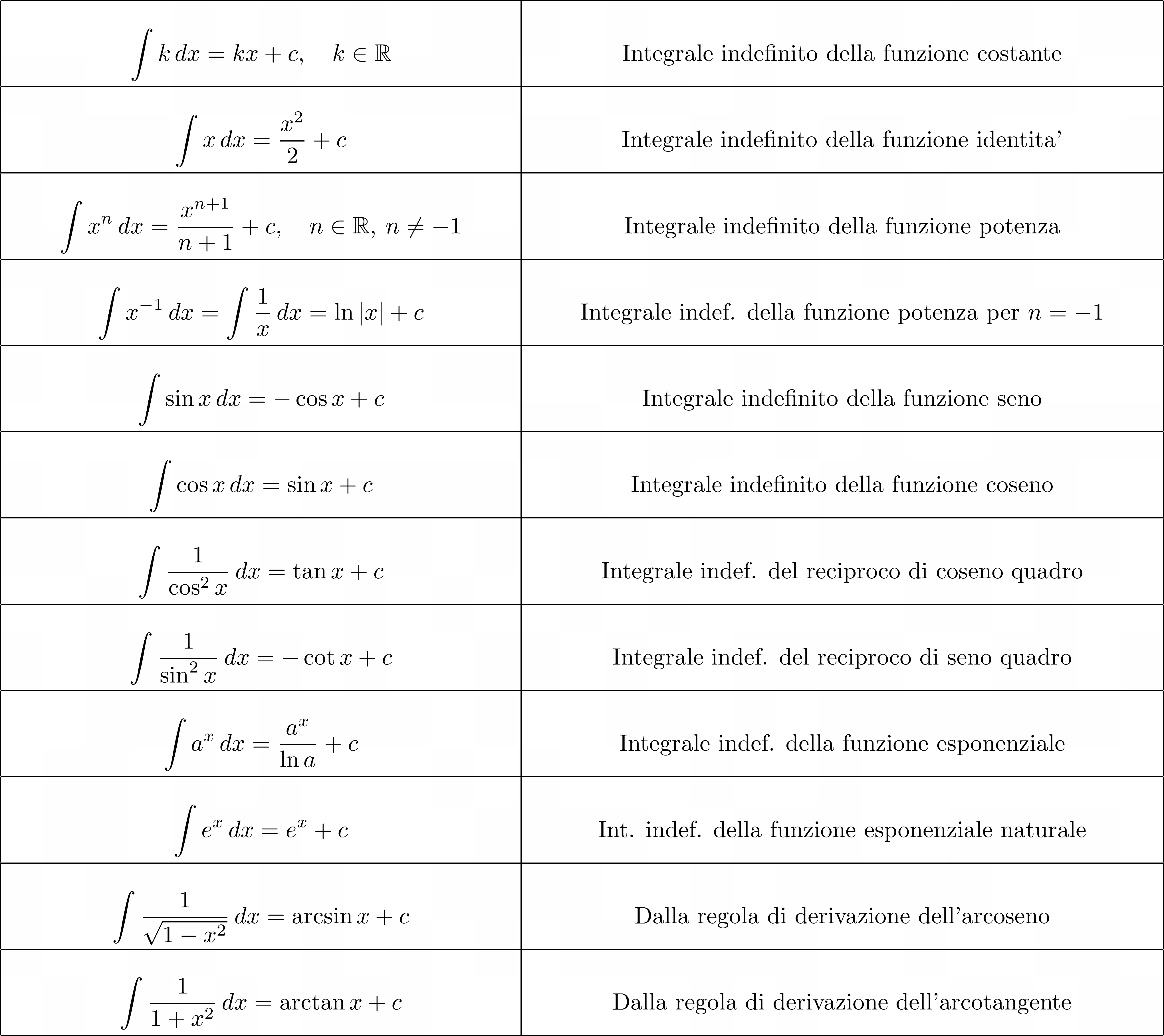
Nella tabella si ha \( c \in \mathbb{R} \) (costante di integrazione). Inoltre con il simbolo \( \ln \) intendiamo il logaritmo naturale, ovvero il logaritmo in base \( e \).
Precisiamo che il calcolo dell’integrale indefinito della funzione identità rientra nel caso dell’integrale indefinito della funzione potenza ponendo \( n=1 \). Tuttavia, abbiamo comunque riportato questo integrale separatamente poiché è decisamente utile impararlo a memoria.
Spendiamo infine due parole per quanto riguarda l’integrale della funzione esponenziale con base generica \( a>0, \: a \neq 1 \):
\[ \int a^x \, dx \]
Per la regola di derivazione della funzione esponenziale si ha:
\[ \dfrac{d}{dx}a^x=a^x \ln a \]
Di conseguenza per la definizione di antiderivata o primitiva possiamo scrivere:
\[ \int a^x \ln a \, dx =a^x+c \]
E’ ora importante osservare che \( \ln a \) è un numero. Di conseguenza possiamo portare fuori tale quantità dal simbolo di integrale:
\[ \ln a\int a^x \, dx =a^x+c \]
Dividendo membro a membro per \( \ln a \) otteniamo in conclusione:
\[ \int a^x \, dx =\dfrac{a^x}{\ln a}+c \]
ritrovando così la regola di integrazione in tabella.
Osserviamo inoltre che per la formula di inversione dei logaritmi si ha:
\[ \log_a e = \dfrac{1}{\log_e a} \]
Di conseguenza possiamo anche riscrivere il precedente integrale come:
\[ \int a^x \, dx ={a^x}{\log_a e}+c \]
Per quanto riguarda gli integrali fondamentali è tutto. Nella prossima lezione parliamo delle regole di integrazione di base. Buon proseguimento con Altramatica! 🙂
