Dopo aver visto la teoria sugli archi associati è bene che ci mettiamo a fare un po’ di esercizi sugli archi associati insieme 😉 Gli esercizi svolti a seguire mostrano le applicazioni delle formule ottenute dai nostri ragionamenti con gli archi associati.
L’obiettivo degli esercizi sugli archi associati è quello di sviluppare le espressioni assegnate utilizzando ciò che sappiamo sugli archi associati, in modo da avere funzioni coseno e seno del solo angolo \( \alpha \).
Pronti? Cominciamo subito con gli esercizi svolti e commentati sugli archi associati! 🙂
Esercizio 1
Utilizzando gli archi associati, riscrivere la seguente espressione in un’espressione equivalente contenente solo \( cos\alpha \) e \( sen\alpha \).
\[ 2sen(\pi-\alpha)+cos(\pi-\alpha)-sen\alpha+3cos\alpha \]
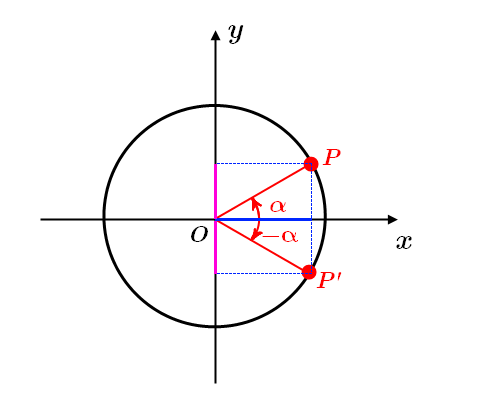
Nell’espressione assegnata compare, oltre all’angolo \( \alpha \), l’angolo \( \pi-\alpha \). Questi due angoli sono associati ed in particolare supplementari, poiché la loro somma è \( \pi \). Dalle considerazioni fatte nella teoria, è chiaro che i punti individuati dai due angoli sulla circonferenza goniometrica avranno la stessa ordinata e ascisse di uguale modulo ma opposto segno.
Siccome le ordinate dei due punti individuati dagli angoli sono uguali, sicuramente:
\[ sen(\pi-\alpha)=sen(\alpha) \]
Poiché le ascisse sono uguali in modulo ma di segno opposto, avremo:
\[ cos(\pi-\alpha)=-cos(\alpha) \]
E’ anche possibile ricordarsi le formule a memoria, questo è chiaro, ma personalmente preferisco fare questi ragionamenti ogni volta. Con un po’ di pratica è facile immaginare gli angoli senza nemmeno doverli disegnare.
Con le relazioni appena scritte, possiamo sviluppare la precedente espressione ottenendo:
\[ 2sen\alpha – cos\alpha -sen\alpha+3cos\alpha=2cos\alpha+sen\alpha \]
L’espressione ottenuta è funzione soltanto dei seni e coseni dell’angolo \( \alpha \), come desiderato.
Esercizio 2
\[ sen\alpha-cos(\pi-\alpha)+cos\alpha-tg(\pi-\alpha)+ctg(\pi-\alpha) \]
L’esercizio riguarda ancora gli angoli supplementari, notiamo tuttavia che sono anche presenti le funzioni trigonometriche tangente e cotangente. Anche queste dovranno essere espresse in funzione del solo angolo \( \alpha \). Come operiamo?
Possiamo sicuramente scomodarci di imparare a memoria le relazioni degli archi associati per le funzioni tangente e cotangente (che qui nemmeno ho trattato), ma un modo più semplice a mio parere è quello di esprimere le funzioni tangente e cotangente in funzione di seno e coseno, quindi utilizzare o ricavare le formule che già conosciamo per seno e coseno.
E’ dunque possibile sviluppare la precedente espressione come segue:
\[ sen\alpha + 2cos\alpha – \frac{sen\alpha}{-cos\alpha}-\frac{cos\alpha}{sen\alpha} \]
ottenendo in conclusione:
\[ sen\alpha+2cos\alpha+tg\alpha-ctg\alpha \]
Esercizio 3
L’esercizio a seguire è molto simile al precedente, per cui mi limito a riportare i passaggi 😉
\[ \begin{align} &[1+tg(\pi-\alpha)](1+tg\alpha)+\frac{sen(\pi-\alpha)cos(\pi-\alpha)}{ctg\alpha}=\\ \\&=\left(1+\frac{sen(\pi-\alpha}{cos(\pi-\alpha)} \right)(1+tg\alpha)+\frac{sen\alpha(-cos\alpha)}{ctg\alpha} = \\ \\ & =\left( 1-\frac{sen\alpha}{cos\alpha}\right)(1+tg\alpha)-sen\alpha \cdot cos\alpha \cdot \frac{sen\alpha}{cos\alpha}= \\ \\&=(1-tg\alpha)(1+tg\alpha)-sen^2 \alpha= \\ \\&=1-tg^2\alpha – sen^2 \alpha \end{align} \]
Infine, utilizzando la relazione fondamentale della trigonometria (\( sen^2\alpha + cos^2\alpha = 1 \)) si ottiene:
\[ 1-tg^2\alpha – sen^2 \alpha = cos^2\alpha-tg^2\alpha \]
Esercizio 4
Determinare un’espressione equivalente alla seguente espressione che sia funzione del solo angolo \( \alpha \).
\[ ctg(\pi+\alpha)tg\alpha-tg(\pi+\alpha)ctg(\pi-\alpha) \]
Ora oltre agli angoli supplementari abbiamo anche angoli la cui differenza è pari a \( \pi \).
Per valutare ad esempio l’espressione:
\[ sen(\pi+\alpha) \]
dobbiamo ricordarci che sulla circonferenza goniometrica i punti individuati su di essa dagli angoli \( \alpha \) e \( \pi+\alpha \) hanno coordinate entrambe uguali in modulo ma di segno opposto.
Quindi, avremo in generale:
\[ sen(\pi+\alpha)=-sen\alpha \]
\[ cos(\pi+\alpha)=-cos\alpha \]
Per risolvere l’esercizio specifico, osserviamo dunque che:
\[ ctg(\pi+\alpha)=\frac{cos(\pi+\alpha)}{sen(\pi+\alpha)}=\frac{-cos\alpha}{-sen\alpha}=ctg(\alpha) \]
\[ tg(\pi+\alpha)=\frac{sen(\pi+\alpha)}{cos(\pi+\alpha)}=\frac{-sen\alpha}{-cos\alpha}=tg(\alpha) \]
Possiamo a questo punto risolvere tranquillamente l’esercizio, poiché ora abbiamo tutto ciò che serve 😉
\[ \begin{align} \\ &ctg(\pi+\alpha)tg\alpha-tg(\pi+\alpha)ctg(\pi-\alpha)= \\ \\ & =ctg\alpha \cdot tg\alpha+tg\alpha \cdot ctg\alpha= \\ \\ & =2\cdot tg\alpha \cdot ctg\alpha = 2 \end{align} \]
Osserviamo infatti che, per le definizioni di tangente e cotangente:
\[ ctg\alpha \cdot tg\alpha = \dfrac{cos\alpha}{sen\alpha} \cdot \dfrac{sen\alpha}{cos\alpha} = 1 \]
Per questo motivo alla fine ci ritroviamo solo con un numero 😉
Esercizio 5
\[ tg(-\alpha)+tg(\pi-\alpha)+tg(2\pi-\alpha)-tg(\pi-\alpha) \]
Nell’esercizio viene introdotto il caso degli angoli opposti. Osserviamo che l’espressione \( tg(-\alpha) \) dovrà essere trattata allo stesso modo dell’espressione \( tg(2\pi-\alpha) \), poiché agli angoli \( -\alpha \) e \( 2\pi-\alpha \) corrispondono gli stessi valori delle funzioni coseno e seno (lo abbiamo visto nella teoria, a proposito degli angoli opposti).
Fatta questa osservazione, ricordandoci che:
\[ sen(-\alpha)=-sen\alpha; \qquad cos(-\alpha)=cos\alpha \]
l’esercizio si risolve come segue:
\[\begin{align} & tg(-\alpha)+tg(\pi-\alpha)+tg(2\pi-\alpha)-tg(\pi-\alpha) =\\ \\ & = -tg\alpha-tg\alpha-tg\alpha+tg\alpha=-2tg\alpha \end{align}\]
Esercizio 6
Vediamo ora un esercizio che contiene degli archi complementari. L’obiettivo è sempre di riscrivere il tutto in funzione del solo angolo \( \alpha \).
\[ cos \left( \frac{\pi}{2}-\alpha\right) \cdot sen \left( \frac{\pi}{2}-\alpha\right) + tg\left( \frac{\pi}{2}-\alpha\right) \cdot sen^2(\pi+\alpha) \]
Osserviamo che assegnati i valori di coseno e seno dell’angolo \( \alpha \), l’angolo \( \dfrac{\pi}{2}-\alpha \) avrà come coseno il \( sen\alpha \) e come seno il \( cos\alpha \). Questo perché considerati i punti P e P’ individuati sulla circonferenza goniometrica dagli angoli \( \alpha \) e \( \left( \dfrac{\pi}{2}-\alpha\right) \) , l’ascissa di P’ è l’ordinata di P, mentre l’ordinata di P’ è l’ascissa di P.
Ancora una volta, preciso che è possibile imparare le formule degli archi associati a memoria, ma io preferisco pensare a come sono questi angoli nella circonferenza goniometrica.
Quindi, tornando all’esercizio assegnato, possiamo sviluppare l’espressione assegnata come segue:
\[ \begin{align}&sen\alpha \cdot cos\alpha +\frac{cos\alpha}{sen\alpha} \cdot (-sen\alpha)^2= \\ \\ & = sen\alpha \cdot \cos\alpha + ctg\alpha \cdot sen^2\alpha = \\ \\ & = sen\alpha \cdot cos\alpha + \frac{cos\alpha}{sen\alpha}\cdot sen^2\alpha = \\ \\ & = 2 \cdot sen\alpha \cdot cos \alpha \end{align} \]
Qua finiscono gli esercizi sugli archi associati. Nella prossima lezione, vedremo come esprimere il seno e il coseno di un angolo in funzione della tangente dell’angolo stesso. Buono studio a tutti con Altramatica! 🙂